Критерий минимаксного риска Сэвиджа

При использовании вышеперечисленных критериев возможны ситуации, когда неконтролируемые факторы будут действовать более благоприятным образом по сравнению с наихудшим состоянием, на которое ориентировалось ЛПР. Например, погодные условия оказываются более благоприятными по сравнению с прогнозируемыми. Количество конкурентов на тех или иных рынках оказывается существенно меньше по сравнению с теми ожиданиями, на которые ориентировались производители.

В подобных ситуациях полезный результат может значительно отличаться от того, который обеспечивается при реализации критерия гарантированного результата или критерия пессимизма.

Поэтому возникает необходимость определения возможных отклонений полученных результатов от их оптимальных значений. Здесь находит применение критерий Сэвиджа. Выбор стратегии аналогичен выбору стратегии по принципу Вальда с тем отличием, что игрок руководствуется не матрицей выигрышей , а матрицей рисков .

Критерий Сэвиджа формулируется следующим образом:

.

Таким образом, критерий Сэвиджа минимизирует возможные потери. Основным исходным допущением этого критерия является предположение о том, что на выбор вариантов обстановки оказывают влияние действия разумных противников (природы), интересы которых прямо противоположны интересам ЛПР. Поэтому, если у противников (конкурентов) имеется возможность извлечь какие-либо преимущества, то они это обязательно сделают. Это обстоятельство заставляет ЛПР обеспечить минимизацию потерь вследствие этих действий.

Пусть задана матрица выигрышей :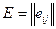

Виды решений	Варианты обстановки
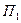
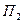
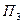
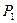
	0,25	0,35	0,40
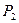
	0,75	0,20	0,30
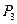
	0,35	0,80	0,10
	0,90	0,20	0,30

Для данной матрицы выигрышей матрица рисков 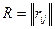будет выглядеть следующим образом:

Виды решений	Варианты обстановки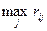
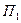
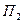
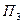
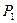
	0,65	0,45	0,00	0,65
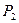
	0,15	0,60	0,10	0,60
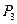
	0,55	0,00	0,30	0,55
	0,00	0,60	0,10	0,60

Показатель эффективности

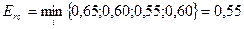
и, следовательно, предпочтение необходимо отдать варианту .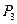

Критерий обобщенного максимина (пессимизма-оптимизма) Гурвица.

Критерий Гурвица позволяет учитывать комбинации наихудших состояний. Этот критерий при выборе решения рекомендует руководствоваться некоторым средним результатом, характеризующим состояние между крайним пессимизмом и безудержным оптимизмом.

В соответствии с этим компромиссным критерием для каждого решения определяется линейная комбинация минимального и максимального выигрышей.

,

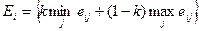и предпочтение отдается варианту решения, для которого окажется максимальным показатель 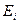, то есть

,

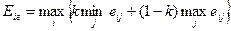где − коэффициент, рассматриваемый как показатель оптимизма .

При 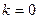критерий Гурвица совпадает с максимальным критерием, то есть ориентация на предельный риск, так как большой выигрыш сопряжен, как правило, с большим риском. При 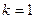− ориентация на осторожное поведение. Значение между 0 и 1 являются промежуточными между риском и осторожностью и выбираются в зависимости от конкретной обстановки и склонности к риску ЛПР.

Проанализируем следующую матрицу выигрышей и при значении коэффициента оптимизма найдем оптимальную стратегию .

Виды решений	Варианты обстановки
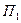
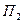
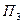
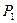
	0,25	0,35	0,40	0,31
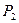
	0,75	0,20	0,30	0,42
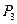
	0,35	0,80	0,10	0,38
	0,90	0,20	0,30	0,48

Показатель эффективности

и, следовательно, предпочтение необходимо отдать варианту .

Применительно к матрице рисков критерий Гурвица имеет вид:

.

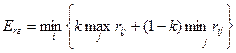Рассмотрим матрицу рисков и при значении коэффициента оптимизма найдем оптимальную стратегию .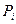

Виды решений	Варианты обстановки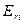
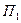
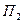
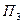
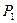
	0,65	0,45	0,00	0,39
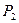
	0,15	0,60	0,10	0,40
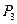
	0,55	0,00	0,30	0,33
	0,00	0,60	0,10	0,36

Показатель эффективности

и, следовательно, предпочтение необходимо отдать варианту .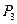

Исследуем зависимость 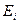от различных значений коэффициента оптимизма и вычислим оптимальное решение для каждого значения .

Решение	Значение коэффициента
0,0	0,2	0,4	0,6	0,8	1,0
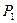
	0,40	0,37	0,34	0,31	0,28	0,25
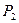
	0,75	0,64	0,53	0,42	0,31	0,20
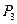
	0,80	0,66	0,52	0,38	0,24	0,10
	0,90	0,76	0,62	0,48	0,34	0,20
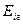
	0,90	0,76	0,62	0,48	0,34	0,25
Оптимальное решение

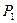
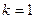Как видно из таблицы, с изменением коэффициента изменяется вариант решения, которому следует отдать предпочтение. При всех , за исключением , предпочтение отдается решению .

Сравним варианты решений в зависимости от применяемых критериев эффективности.

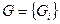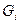Пусть при выборе эффективных решений при наличии неуправляемых факторов используется множество критериев оптимальности , . Составляющими могут быть критерии: гарантированного результата, Сэвиджа, пессимизма и т.д.

Критерии 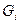являются функцией управляемых факторов 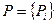, 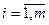и неуправляемых факторов 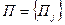, 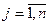. Располагая множеством критериев 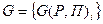, необходимо выбрать эффективное решение с учетом указанной совокупности решений.

Проанализируем сквозной пример, приведенный в этом параграфе. Лучшие стратегии: по критерию гарантированного результата ─ 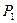, по критерию оптимизма ─ , по критерию пессимизма ─ 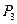, по критерию Сэвиджа ─ 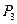, по критерию Гурвица при ─ .

Поскольку стратеги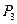и и фигурируют в качестве оптимальных по два раза, то к практическому применению можно рекомендовать или стратегию 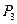или . Вместе с тем, стратегия 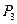является более осторожной и скорее всего ЛПР выберет ее.

Анализ решений при многих критериях в значительной степени сводится к организации в той или иной форме взаимодействия с ЛПР, которое одно только и может разрешить проблему соизмерения различных критериев. Тем не менее, существует довольно ограниченная область, в которой применение сугубо формального анализа без обращения к ЛПР оказывается весьма полезным. Речь идет о выделении так называемого множества эффективных, или оптимальных по Парето, альтернатив.

Эффективной считается такая альтернатива, для которой не существует другой допустимой, не уступающей ей по всем критериям и хотя бы по одному критерию превосходящей ее.

Рассмотрим применение этого принципа на примере. Пусть задана матрица выигрышей :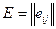

Виды решений	Варианты обстановки
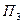
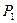
	0,25	0,35	0,40
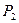
	0,75	0,20	0,30
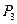
	0,35	0,80	0,10
	0,90	0,20	0,30

Для данной матрицы выигрышей матрица рисков 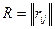будет выглядеть следующим образом:

Виды решений	Варианты обстановки
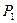
	0,65	0,45	0,00
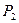
	0,15	0,60	0,10
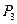
	0,55	0,00	0,30
	0,00	0,60	0,10

В качестве критериев эффективности предлагается взять ожидаемый выигрыш и ожидаемый риск. Решение, которое имеет наибольший ожидаемый выигрыш и наименьший ожидаемый риск будет оптимальным по Парето. Для того, чтобы рассчитать ожидаемый выигрыш и ожидаемый риск необходимо задать распределение вероятностей для состояний природы. Так как мы рассматриваем ситуацию неопределенности, то распределение вероятностей нам не известно. В условиях полной неопределенности, когда вероятности рассматриваемых ситуаций неизвестны, можно пользоваться правилом Лапласа, заключающимся в том, что все неизвестные вероятности считаются равными. Подобный критерий принятия решения можно назвать принципом недостаточного обоснования Лапласа.

Рассчитаем ожидаемый выигрыш для каждой из четырех стратегий.

,

,

,

.

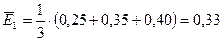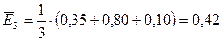Максимальный ожидаемый выигрыш равен 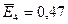и соответствует стратегии .

Рассчитаем теперь ожидаемый риск для каждой из четырех стратегий.

,

,

,

.

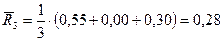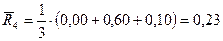Минимальный ожидаемый риск равен и соответствует стратегии .

Таким образом, стратегия является оптимальной по Парето.

Рассмотрим матричную игру с нулевой суммой[3] представленную платежной матрицей:

.

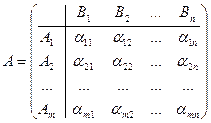Построим оптимальные стратегии игроков и 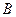. Пусть игрок выбирает некоторую стратегию 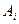, тогда, в наихудшем случае (например, если выбор станет известен игроку 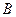), он получит выигрыш равный 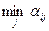. Предвидя эту возможность, игрок должен выбрать такую стратегию, чтобы максимизировать свой минимальный в каждой стратегии выигрыш . Таким образом,

.

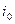Величина называется нижней ценой игры ( ─ это гарантированный выигрыш игрока ). Очевидно, находится в одной из строк матрицы , пусть в строке , тогда стратегия называется максиминной.

С другой стороны, противник ─ игрок 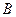, заинтересован в том, чтобы обратить выигрыш игрока в минимум, поэтому он должен пересмотреть каждую свою стратегию с точки зрения максимального выигрыша игрока при этой стратегии. Другими словами, при выборе некоторой стратегии 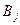он должен исходить из максимального проигрыша в этой стратегии, равного 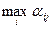, и найти такую стратегию, при которой этот проигрыш будет наименьшим, то есть не более чем

.

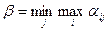Величина 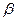называется верхней ценой игры, а соответствующая ей стратегия 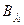─ минимаксной.

Принцип осторожности, диктующий игрокам выбор стратегий максиминной или минимаксной соответственно, в теории игр именуют принципом «минимакса», а сами стратегии ─ общим термином «минимаксные стратегии».

Если игра одноходовая, то есть партнеры играют один раз, выбирая по одной чистой стратегии, то в расчете на разумно играющего противника они должны придерживаться принципа минимакса. Это гарантирует выигрыш 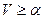игроку и проигрыш игроку 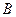. Следовательно, при применении минимаксных стратегий величина платежа 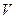ограничена неравенством .

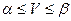Вполне определенной игрой или игрой с седловой точкой называется игра, у которой совпадают нижняя и верхняя цены игры, то есть выполняется равенство:

.

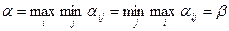При этом 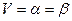называется ценой игры, а элемент 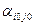, соответствующий равенству, называется седловой точкой

Простота решения игры с Седловой точкой заключается в том, что оптимальные стратегии обоих игроков находятся сразу. Для игрока это стратегия , для игрока 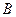─ 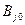. Причем, такое решение обладает свойством устойчивости в том смысле, что, если один из игроков применяет свою оптимальную стратегию, то любое отклонение другого игрока от оптимальной стратегии может оказаться не выгодным для него.

Если же игра повторяется неоднократно, то постоянное применение минимаксных стратегий становится неразумным. Например, если игрок 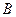будет уверен в том, что на следующем ходу применит прежнюю стратегию, то он несомненно выберет стратегию, отвечающую наименьшему элементу в этой строке, а не прежнюю.

Таким образом, мы пришли к выводу, что при неоднократном повторении игры обоим игрокам следует менять свои стратегии. Тогда возникает вопрос: а каким образом их менять, чтобы в среднем выигрыш одного и проигрыш другого был аналогично одноходовой игре, ограничивались снизу и сверху соответственно?

Для ответа на этот вопрос введем вероятность (относительную частоту) применения игроком i -й стратегии, и ─ вероятность применения j -й стратегии игроком 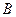. Совокупности этих вероятностей определяют векторы 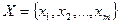, где и , где . Эти векторы или наборы вероятностей выбора чистых стратегий называются смешанными стратегиями игроков.

Для получения ограничений на средний выигрыш или проигрыш рассмотрим математическое ожидание выигрыша первого игрока

.

Основная теорема теории игр утверждает: каждая матричная игра с нулевой суммой имеет, по крайней мере, одно решение, возможно в области смешанных стратегий, то есть существуют стратеги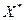и и , оптимальные для обоих игроков, причем

.

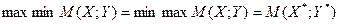Число называют ценой игры.

И если один из игроков придерживается своей оптимальной стратегии, то выигрыш (проигрыш) его остается неизменным независимо тактики другого игрока, если последний не выходит за пределы своих «полезных» стратегий, иначе выигрыш (проигрыш) возрастает.

Это означает выполнение неравенств

,

.

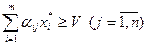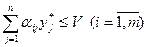Эти неравенства будут необходимы при сведении матричной игры к задаче линейного программирования.

Для отыскания оптимальных смешанных стратегий игроков сведем матричную игру к задаче линейного программирования. Положим:

и .

Тогда отыскание оптимальной смешанной стратегии игрока приводит к необходимости решения следующей задачи линейного программирования:

при условиях

, ; , .

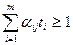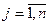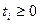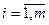Положим:

и .

Тогда отыскание оптимальной смешанной стратегии 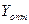игрока 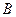приводит к необходимости решения следующей задачи линейного программирования:

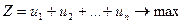
при условиях

, ; , .

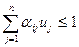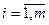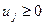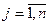Исходя из основной теоремы теории двойственности, эти задачи имеют конечное решение и .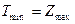

Дата добавления: 2014-11-29