Фігури нульової площі

З означення квадровних фігур випливає, що якщо зовнішня площа фігури Ф дорівнює нулю: 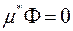, то сама фігура є квадровною (бо 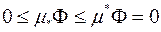) і

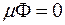
Теорема 1.6. (напівадитивність верхньої міри). Для довільних фігур 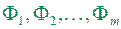Ф₁, Ф₂, …,Ф _m площини має місце нерівність:

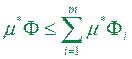(1.16)

де .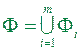

Доведення. Оскільки кожний квадрат 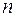-го рангу, який має принаймні одну спільну точку з 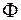, має принаймні одну спільну точку з деякою множиною , то

.

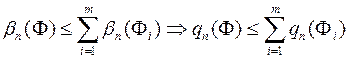В останній нерівності перейдемо до границі при :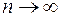

■

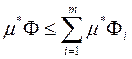З теореми, зокрема, випливає, що об’єднання довільної скінченної множини квадровних фігур нульової площі є фігура нульової площі.

Приклад 6. Множина 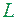точок справнювальної дуги Жордана є фігура нульової площі.

Теорема 1.7. Для того, щоб фігура була квадровною, необхідно і достатньо, щоб межа 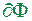була квадровною і мала площу 0.

Теорема 1.8. Для того щоб обмежена множина 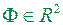була квадровною, необхідно і досить, щоб для довільного ε >0 існувала скінченна система прямокутників 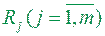попарно без спільних внутрішніх точок, і така: 1) яка б покривала усі межові точки множини і 2) сума площ прямокутників цієї системи була б меншою від .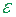

Доведення прикладу 6 і теорем 1.7-1.8 можна знайти в підручниках [Кудр., ст. 293-], [Давидов, ст.106], [Райков, Многом., ст. 153-154], [Никольський С.М. Курс м/а.: В 2-х т. –М.: Наука, 1973.-Т. 2]

Теорема 1.9. Об’єднання, перетин і різниця двох квадровних фігур є фігура квадровна.

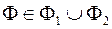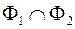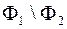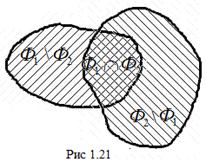
Доведення. Якщо , , або то 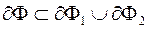(рис. 1.21) Оскільки фігури 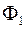і 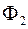квадровні, то , також .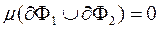

Тому 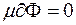і за теоремою 1.7 фігура 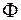квадровна. ■

Зауваження. Теорему 1.9 можна поширити на об’єднання і перетин довільної скінченної множини квадровних фігур, при чому .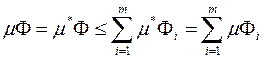

Теорема 1.10 (адитивність міри). Площа фігури, яка є об’єднаннями скінченного числа квадровних фігур 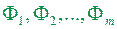, які попарно не перетинаються, дорівнює сумі площ цих фігур:

.

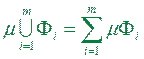Доведення. Оскільки для довільного n правильне включення 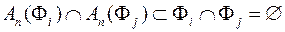, , 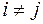то і 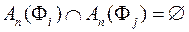, , 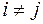тому згідно з (1.2)

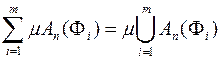. (1.7)

Якщо квадрат рангу 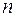належить множині , то він належить і об’єднанню 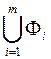цих множин, отже

,

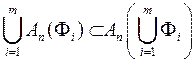Звідки в силу монотонності міри і рівності (1.17), випливає:

.

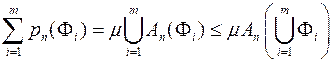Перейдемо до границі при :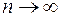

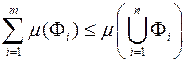. (1.18)

З іншого боку, для довільних відмінних множин має місце нерівність (1.16) ()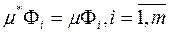

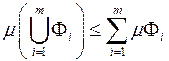(1.19)

З нерівностей (1.18) і (1.19) і випливає потрібна рівність. ■

Дата добавления: 2014-11-29