Число степеней свободы системы

Две материальные точки, которые должны оставаться на неизменном расстоянии друг от друга образуют простейшую механическую систему (рис. 1.5).

Будем условно говорить, что точки связаны стержнем неизменной длины. Число степеней свободы такой системы равно 5, если внешние связи отсутствуют. Действительно, каждая точка системы, если бы она была свободной, имела бы 3 степени свободы. То есть две точки вносят в систему 6 степеней свободы. Наложение одной геометрической связи снимает 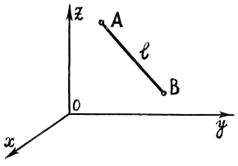одну степень свободы системы.

Положение такой системы в пространстве можно определить, задав 5 каких-нибудь параметров, например 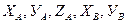. Недостающая координата 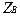найдётся из уравнения связи:

Рис. 1.5

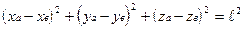. (1.2)

Наложение внешних связей уменьшит число степеней свободы рассматриваемой системы, причём каждая геометрическая связь – на единицу. Поэтому число степеней свободы S этой простейшей механической системы может быть в пределах от 0 до 5 (рис. 1.6, 1.7).

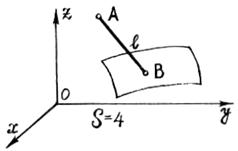Рис. 1.6

Рис. 1.7

В общем случае, если система состоит из 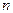точек в пространстве и на неё наложено 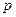геометрических связей, то число степеней свободы такой системы можно подсчитать по формуле:

. (1.3)

А если все точки системы расположены на некоторой неподвижной поверхности f (x; y; z) = 0, то

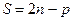. (1.3')

Для определения положений в пространстве всех ее точек в отдельности (следовательно всей системы в целом) нужно задать s независимых параметров.

1.4. Число степеней свободы твёрдого тела

Твёрдое тело можно рассматривать как механическую систему, состоящую из бесконечно большого числа точек, на которую наложено бесконечно много внутренних связей (постоянство расстояний между всеми его точками). Определить число степеней свободы твёрдого тела, пользуясь формулой (1.3), неудобно. Поэтому рассмотрим различные случаи движения тела и воспользуемся тем, что уже известно нам из кинематики:

а) твёрдое тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы: ему можно сообщить возможное перемещение поворотом на угол 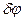в одну или другую сторону. Эти возможные перемещения, конечно, не являются независимыми. Из кинематики известно, что положение такого тела в пространстве определяется одной угловой координатой ;

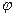б) твёрдое тело, совершающее в пространстве поступательное движение, имеет до трёх степеней свободы, т.к. все точки такого тела движутся одинаково, то достаточно знать движение (и положение в пространстве) одной какой-нибудь её точки. Если на такое движение наложены дополнительные ограничения (связи), то число степеней свободы уменьшается. Например, ползун, движущийся по какой-то направляющей (поршень внутри цилиндра), имеет одну степень свободы, как и отдельно взятая точка (рис. 1.8);

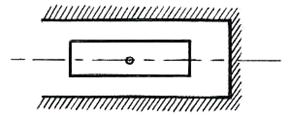
Рис. 1.8

в) тело, совершающее плоскопараллельное движение, имеет 3 степени свободы. Действительно, если таким телом является плоская фигура, то саму эту плоскость определяют три её точки (через три точки можно провести единственную плоскость). Каждая такая точка, движущаяся на плоскости, имеет 2 степени свободы. На эти точки наложены 3 связи (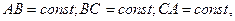 рис. 1.9). Поэтому .

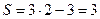Из кинематики известно, что положение плоской фигуры на плоскости определяется тремя параметрами: 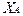, , 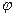(где 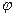– угол поворота тела вокруг полюса А). Можно было бы использовать и другие

Рис. 1.9

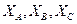пара-метры для определения положения плоской фигуры, например . Недостающие координаты точек 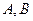и 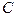найдутся из трех уравнений вида (1.2);

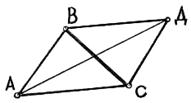г) покажем, что свободное твёрдое тело имеет 6 степеней свободы. Простейшее твёрдое тело состоит из трёх точек 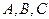(рис. 1.10).

Рис. 1.10

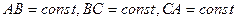При этом . Каждая свободная точка вносит в систему 3 степени свободы. Наложение трёх геометрических связей уменьшает на 3 единицы число степеней свободы. Таким образом, в данном случае

.

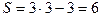Присоединение к этому телу четвёртой точки (точка ) даёт дополнительно и тут же снимает по 3 степени свободы, т.е.

.

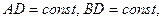
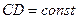И у такого тела .

Добавление следующей точки ничего не изменит ни в рассуждениях, ни в результате. Итак, свободное твёрдое тело имеет 6 степеней свободы. Конечно, к этому выводу можно было придти иным путём. Например, исходя из того, что такое тело может совершить 6 независимых между собой движений (вдоль осей – поступательных, и вокруг этих же осей – вращательных). Не случайно и то, что для равновесия такого тела в статике было получено 6 независимых уравнений равновесия.

1.5. Обобщённые координаты

Из рассмотренных случаев движений точки (тела, системы) следует, что их положение в пространстве однозначно определяется заданием такого количества независимых между собой параметров, сколько степеней свободы имеет, эта точка (тело, система) в конкретных условиях (т.е. с учётом наложенных связей). Ими необязательно являются декартовы координаты точек. Например, в случае вращения тела вокруг неподвижной оси – это угол поворота 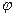тела, а в случае плоскопараллельного движения тела – декартовы координаты одной точки тела (полюса) и угол поворота тела вокруг него (). В общем случае эти параметры могут иметь любой геометрический смысл, они должны быть независимы между собой и однозначно определять положение всех точек (тела или системы в целом). Такие параметры называются обобщёнными координатами данной точки (данного тела, системы). Условимся в дальнейшем обозначать их, как 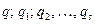, где 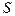– число степеней свободы точки (тела, системы).

Так как положение точек обычно определяется либо их радиус-векторами , либо прямоугольными координатами 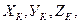то они должны однозначно выражаться через обобщённые координаты некоторыми выражениями вида:

(1.4)

или

(1.5)

Их конкретный вид зависит от самих систем, от наложенных связей и от тех параметров, которые приняты за обобщённые координаты.

Рассмотрим некоторые примеры.

Пример 1

Кривошипно-ползунный механизм (рис. 1.11) состоит из кривошипа 1, шатуна 2 и ползуна 3. Между собой они соединены шарнирами и (внутренние связи). Кроме этого на эту систему наложены внешние связи (шарнир О, направляющие ползуна 3). Все звенья и точки механизма движутся, оставаясь в плоскости рисунка: ; .

Определим число степеней свободы этого механизма.

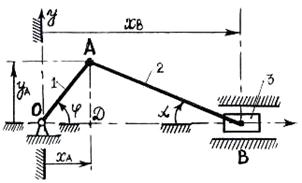
Рис. 1.11

Кривошип может вращаться вокруг неподвижной точки О (одна степень свободы); ползун 3 может двигаться поступательно вдоль направляющих (ещё одна степень свободы). Эти тела связаны между собой шатуном так, что 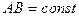(одна удерживающая геометрическая связь). Следовательно, число степеней свободы механизма S = (1 + 1 – 1) =1.

В качестве обобщённой координаты можно взять один из следующих параметров (см. рис. 1.11):

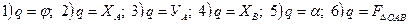( – площадь треугольника ОАВ).

Рассмотрим первый случай и выразим через 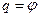координаты точек .

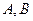Имеем по рисунку:

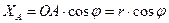(а)

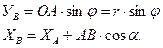(б)

Чтобы выразить 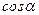через 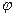рассмотрим прямоугольники и 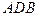. Они – прямоугольные. Их общий катет a.
Поэтому .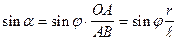

Следовательно:

.

Итак:

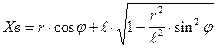. (в)

Если в качестве обобщенной координаты принять 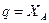, то получаем:

;

;

.

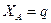Аналогично предыдущему случаю находим:

;

;

.

Итак,

,

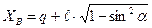где .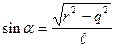

Как видим, декартовы координаты через принятые обобщённые координаты выражаются различными уравнениями. В некоторых случаях эти выражения весьма громоздкие. Это свидетельствует о неудачном выборе обобщённой координаты. Однако, важно то, что через принятую обобщённую координату можно найти декартовы координаты всех точек системы. Например, продолжив выкладки, можно выразить и координаты любой точки 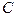шатуна через принятую .

Дата добавления: 2014-11-29