Основные теоретические сведения 1 страница

ПАРНАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ

В общем случае регрессия – функциональная зависимость между объясняющими переменными Х_j и объясняемой переменной Y, которая строится с целью прогнозирования среднего значения Y при заданных значениях Х_j =x_j, 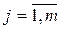или для анализа влияния отдельных переменных Х_j, 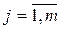на зависимую переменную.

Различают уравнения регрессии I и II рода.

Уравнением регрессии первого рода называют уравнение вида:

. (1.1)

Если уравнение (1.1) представляет собой уравнение связи двух случайных величин Y и Х, то это уравнение представляет собой уравнение парной регрессии. В предположении нормального распределения случайной величины (Y, Х) парную регрессию называют линейной парной регрессией, т.к. в этом случае условное математическое ожидание (1.1) представляет собой уравнение прямой линии

Y = M (Y / x) = ₀ + ₁ Х. (1.2)

Для точного описания уравнения регрессии необходимо знать условный закон распределения зависимой переменной Y при условии, что переменная Х примет значение х. В связи с тем, что реальные значения переменной Y не всегда совпадают с ее средним значением M (Y / x), то в уравнение регрессии вводится случайная составляющая 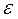. Тогда уравнение (1.2) можно записать в виде:

Y^* = M (Y / x) + 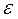(1.3)

или для конкретных наблюдений (у _i, x _i):

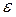= ₀ + ₁ x_i + _i, 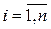. (1.4)

Уравнение (1.4) называют теоретической линейной моделью.

Возмущения 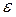_i, 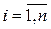должны удовлетворять основным предпосылкам регрессионного анализа:

1. Математическое ожидание возмущения 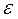_i равно нулю

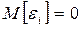
или

₀ + ₁ x_i.

2. Дисперсия возмущения 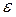_i постоянна для любого i, т.е.

, .

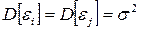3. Возмущения 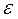_i и 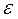_j являются независимыми друг от друга, что влечет за собой отсутствие автокорреляции

.

4. Возмущения 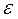_i представляет собой нормально распределенную случайную величину.

Обычно исследователь имеет дело с исходными данными выборки объемом n, где каждое наблюдение – есть точка (Y, Х) в (m +1) – мерном пространстве. Здесь m – число объясняющих переменных.

В случае парной регрессии имеется выборка объемом n двумерной случайной величины (Y, Х).

Уравнением регрессии второго рода называют эмпирическое уравнение регрессии, которое строится на основе данных выборки.

Рассматривается парная линейная регрессия, когда уравнение регрессии второго рода имеет вид

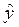_i = М [ Y/X=x ] = b ₀ + b ₁ x_i, 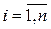. (1.5)

С учетом уравнения (1.3) эмпирическую линейную модель связи переменных Y и Х запишем в виде:

y_i = b ₀ + b ₁ x_i + e_i, (1.6)

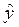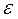где _i, b ₀, b ₁, e _i – оценки соответственно y_i, ₀, ₁, _i.

Построение уравнения регрессии начинается с построения корреляционного поля, представляющего собой графическую зависимость в виде точек случайной величины (Y, Х) на плоскости y 0 x. По расположению эмпирических точек делается вывод о наличии линейной корреляционной зависимости между переменными Y и Х. Дальнейшее построение уравнения регрессии сводится к оценке ее параметров, используя метод наименьших квадратов (МНК). В этом случае неизвестные параметры b ₀ и b ₁ выбираются так, чтобы сумма квадратов отклонений эмпирических значений y_i от значений 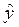_i, найденных по уравнению регрессии (1.5), была минимальной

min.

Применение МНК обусловлено тем, что он позволяет получить несмещенные оценки с минимальной дисперсией, в условиях, когда 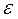_i удовлетворяют всем предпосылкам регрессионного анализа.

В результате операции МНК оценка выборочного коэффициента регрессии b ₁ определяется выражением:

b ₁ = Cov (X, Y) / , (1.7)

а коэффициента b ₀:

b ₀ = , (1.8)

где = у_i / n; = х_i / n; Cov (X, Y) = ; = .

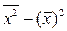Точность оценок коэффициентов линейного уравнения регрессии первого рода характеризуется их выборочными дисперсиями, которые вычисляются по формулам:

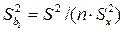, (1.9)

. (1.10)

Здесь S ² – дисперсия регрессии – оценка дисперсии , определяемая по формулам: S ² = е_i ² /(n – 2), е_i = y_i - b ₀ - b ₁ x_i.

Проверка качества уравнения регрессии осуществляется по ряду позиций.

1. Оценка статистической значимости коэффициентов регрессии заключается в проверке основной гипотезы Н ₀ о значимости отличия коэффициентов b ₀ и b ₁ от нуля. С этой целью используется критерий Стьюдента. Вычисляются , 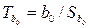и сравниваются с t_крит. Результатом сравнения является вывод о значимости коэффициентов b ₀ и b ₁.

2. Интервальные оценки коэффициентов уравнения регрессии.

Так как объем выборки ограничен, то b ₀ и b ₁ – случайные величины, поэтому желательно найти доверительные интервалы для истинных значений 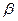₀, ₁. Для этого также используется статистика

, i = 0,1,

которая имеет t – распределение Стьюдента с степенями свободы. Интервальные оценки параметров _i при заданном уровне значимости 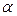имеют вид

, i = 0,1,

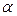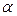с надежностью р = 1- . Здесь t_крит – критическое значение распределения Стьюдента, взятое из таблицы с параметрами и /2.

3. Проверка значимости уравнения регрессии в целом.

Позволяет установить, соответствует ли математическая модель экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных для описания зависимой переменной. Проверка значимости уравнения регрессии производится на основе дисперсионного анализа. Мерой общего качества уравнения регрессии является коэффициент детерминации R²:

R ² = 1 - 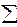е_i ² / (y_i - )². (1.11)

Выражение (1.11) вытекает из соотношения:

(y_i - )² = k_i ² + 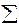e_i ², (1.12)

где k_i ² = ( _i - )² – объясненная регрессией сумма квадратов. Характеризует разброс, обусловленный регрессией;

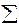e_i ² = 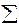(y_i - _i)² – остаточная (необъясненная) сумма квадратов – характеризует случайную составляющую разброса y_i относительно линии регрессии .

Из соотношений (1.11) и (1.12) следует, что коэффициент детерминации R ² есть не что иное, как:

R ² = k_i ² / (y_i - )². (1.13)

Таким образом, коэффициент детерминации можно вычислить по (1.11) или по (1.13).

Основная цель использования уравнения регрессии - прогноз значений зависимой переменной.

Здесь речь идет о возможных значениях Y_р при определенных значениях объясняющей переменной Х_р. Так как задача решается в условиях неопределенности то прогноз удобнее всего давать на основе интервальных оценок, построенных с заданной надежностью .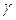

Причем здесь возможно два подхода: 1) предсказание среднего значения, т.е. M (Y / Х = x_р); 2) предсказание индивидуальных значений Y / Х = x_р.

Интервальный прогноз для среднего значения вычисляется следующим образом:

_р t_кр S , (1.14)

где 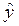_р = b ₀ + b ₁ x_р; t _кр – критическое значение, полученное по распределению Стьюдента при количестве степеней свободы = n – 2 и заданной вероятности /2.

Интервальный прогноз для индивидуального значения вычисляется по формуле:

_р t_кр S 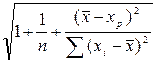. (1.15)

1.2. Реализация задания на компьютере с помощью ППП Ехсеl

С целью повышения эффективности решения задачи необходимо воспользоваться возможностями ППП Ехсеl. Для этого требуется инициировать опцию Мастер функций. В основном будет востребована категория Статистические и некоторые функции из категорий Математические и Ссылки и массивы. Перечень этих функций и краткое описание представлены в Приложении «Стандартные функции».

ВНИМАНИЕ! Каждый студент должен выполнить индивидуальное задание с использованием компьютера в двух вариантах:

1) Реализовать формулы (1.1) – (1.15) с помощью ППП Ехсеl.

2) Использовать «комплексные» функции, выходом которых являются не только коэффициенты регрессии, но и дополнительная регрессионная статистика (среднеквадратические отклонения, коэффициент детерминации и т.д.).

1) Реализация регрессионных формул (1.1) – (1.15).

В начале необходимо воспользоваться Мастером диаграмм, выбрать тип Точечная и нанести значения выборки на корреляционное поле (рис. 1.1). По расположению точек на графике сделать предварительный анализ о возможной линейной зависимости между переменными.

С помощью функций ППП Ехсеl определить оценки коэффициентов регрессии b ₀, b ₁, реализуя формулы (1.7), (1.8), например , вычисляются с помощью функции СРЗНАЧ, а с помощью функции СУММПРОИЗВ()/ n. Для вычисления 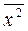можно воспользоваться соотношением СУММКВ(число1;число2;...) / n. Однако составляющие коэффициента b ₁ можно вычислить проще, через Статистические функции КОВАР(массив1; массив2) Cov (X, Y) и ДИСПР S_x ² или СТАНДОТКЛОНП S_x ².

По соответствующим формулам вычисляются дисперсии 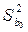, и на основании Т -статистик делается вывод о значимости коэффициентов регрессии и определяются их доверительные интервалы. Значения t_кр можно получить, используя статистическую функцию СТЬЮДРАСПОБР.

Рис. 1.1.

Примерный вид реализации задачи на компьютере представлен на рис.1.2.

Для графической иллюстрации приближения корреляционной функции и выборочных данных y_i воспользуемся Мастером диаграмм (Точечная) (см. рис.1.3.).

Параметры линейной регрессии можно рассчитать и сразу. Для этого в Ехсеl существуют функции Наклон и Отрезок. Функция Наклон служит для определения углового коэффициента связи (b ₁), а функция Отрезок – для определения свободного члена уравнения (b ₀). В качестве аргументов этих функций вводятся массивы Х и Y.

Кроме перечисленных возможностей существует еще и следующая возможность. Построим график по имеющимся данным. Чтобы ось Х отражала фактические данные, выберем тип диаграммы Точечная. На построенной диаграмме выделим график функции, щелкнув по ней левой кнопкой мыши. Затем нажмем правую кнопку мыши, выведем контекстное зависимое меню, в котором выберем опцию Добавить линию тренда. В панели линии тренда во вкладке Тип надо выбрать тип функции (по умолчанию выбирается Линейная). Во вкладке Параметры введем название тренда (теоретической кривой) и установим флажки «Показывать уравнение на диаграмме» и «Поместить на диаграмму величину достоверности аппроксимации (R^2)». В результате появится график вида (рис.1.4.).

		Парная регрессия(пример)
		y = b0 + b1*x
Введите исходную информацию
Территория	Прожиточный	Среднемесячн	Оценка У	Ошибки Е
региона	минимум (х)	зарплата (у)
			148,7700683	-15,77006831
			152,4517905	-4,45179052
			157,0539433	-23,05394328
			149,6904989	4,309501138
			158,8948044	3,105195612
			174,5421238	20,45787622
			138,6453322	0,354667771
			157,9743738	0,025626164
			144,1679155	7,832084455
			157,0539433	4,946056717
			146,9292072	12,0707928
			182,8259988	-9,825998758
Вычисление по формулам		Al
				0,05
Вспомогательные параметры			Кэфф. регрессии
Хср	Уср	ХУср	ХквСр		В0	В1
85,58333333	155,75		7492,25		76,9764852	0,92043055
КвХср	ЕквСр	УквСр	КвУср		Кху	Rкв
7324,506944	131,2435245	24531,41667	24258,0625		0,72102521	0,51987736
Тв1	Тв0	Ткр	Sb0Кв	Sb1Кв	SКв
3,290594434	3,179327594	2,433444024	586,1997046	0,078240809	157,492229

Рис.1.2.

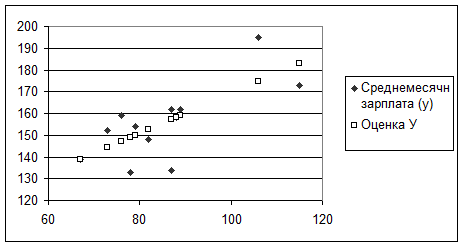
Рис.1.3.

Рис.1.4.

2) Использование «Комплексных» функций.

Одной из таких функций является встроенная статистическая функция ЛИНЕЙН (описание функции и ее аргументов приведено в приложении «Стандартные функции»).

Дополнительная регрессионная статистика (в случае ее инициализации) будет выводиться в порядке, указанном в следующей схеме:

Значение коэффициента b1	Значение коэффициента b0
Среднеквадратическое отклонение b1	Среднеквадратическое отклонение b0
Коэффициент детерминации R^2	Среднеквадратическое отклонение у
F - статистика	Число степеней свободы
Регрессионная сумма квадратов	Остаточная сумма квадратов

Для данных из вышерассмотренного примера результат вычисления функции ЛИНЕЙН представлен на рис.1.5.

Территория	Прожиточный	Среднемесячн
региона	минимум (х)	зарплата (у)		0,920431	76,97649
				0,279716	24,21156
				0,519877	12,54959
				10,82801
				1705,328	1574,922

Рис.1.5.

Примечание. Функция ЛИНЕЙН должна быть введена, как формула массива в интервал с необходимым количеством строк и столбцов. Перед использованием функции ЛИНЕЙН выделяем ячейку (1,1) (1-ая строка, 1-ый столбец) массива, в который будет занесен результат вычисления функции, затем инициализируем Мастер функций, выбираем категорию Статистические и функцию Линейн. Щелкните по кнопке ОК. После заполнения аргументов в ячейке (1,1) появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, выделите массив нужной размерности, включая и ячейку (1,1) (в нашем примере 5 – строк, 2 – столбца), нажмите на клавишу <F2>, а затем – на комбинацию клавиш <CTRL>+<SHIFT>+<ENTER>.

Для лучшей наглядности можно нужные значения из этой таблицы выбирать индивидуально и размещать в нужных форматах документа. Для этого можно воспользоваться функцией ИНДЕКС из категории Ссылки и массивы. Выделите ячейку, в которую хотите поместить отдельный элемент массива и введите формулу, например: Индекс (Линейн (Y; Х; Истина; Истина); 1; 2).

Дата добавления: 2014-11-29