Графоаналітичний метод лінійного програмування та оптимізація технологічних процесів

Під оптимізацією виробничих процесів розуміють прийняття такого рішення, яке при найменших затратах ресурсів або при їх обмеженнях давало б оптимальні результати. Математично це означає, що треба знайти екстремальний (мінімальний, максимальний) розв'язок задачі.

Такі задачі розв'язують графічним методом лінійного програмування.

Нехай виробничий процес визначається двома змінними факторами х і у. Позначимо ознаку виробничого процесу, яку оптимізують, через L. Запишемо виробничу функцію (L зв'язана з х і у лінійно):

L = с_хх + с₂у + с₀. (2.52)

Треба знайти екстремальне значення L при обмеженнях відносно змінних факторів виробництва х і у, які виражаються нерівностями:

Областю розв'язку кожної з цих нерівностей є одна з двох півплощин, які розділяються прямою а_i1х + а_i2у = в_і (і=1,2,...,т). Вибір з двох півплощин тієї, що відповідає а_i1х + а_і2у ≥b_t, виконується зведенням цього виразу до вигляду

y ≥ - (a_i1/a_i2)x₁+b_i/ a_i2 або у< - (а_i1 / а_і2)х₁+в_і / а_і2. Перетин т таких площин утворюють многокутну область D, яку називають областю визначення розв'язків системи нерівностей (2.53). Ця область може бути обмеженою, необмеженою і навіть порожньою. Останній випадок з'являється тоді, коли система нерівностей некоректна. У системі може бути зайва нерівність, якій відповідає пряма, що не має з областю D спільних точок. Область розв'язків D є опуклою. Пряма, яка має з областю D хоча б одну спільну точку, причому так, що вся область лежить по один бік від цієї прямої, називається опорною відносно цієї області.

Із області D треба відшукати такі додатні значення x і у, при яких функція L приймає екстремальне значення. Для кожної фіксованої точки (x_iу_і) площини функція L приймає конкретні значення L. Множина всіх таких точок є пряма

L₁=с₁х + с₂у + с₀, перпендикулярна вектору с(c₁,с₂), що виходить з початку системи координат. Якщо пряму L, переміщувати паралельно самій собі вздовж позитивного напрямку вектора с, то функція L зростатиме, а якщо у протилежному напрямку - спадатиме. При переміщенні прямої L уздовж позитивного напрямку вектора с вона вперше перетне вершину многокутника області D, де функція L приймає мінімальне значення. При подальшому переміщенні пряма перетне останню вершину многокутника, в якій функція приймає максимальне значення. Таким чином, вершини многокутника області D розв'язків є опорними точками прямої L, в яких функція приймає екстремальні значення. Опорна пряма може мати з многокутником області D лише одну спільну точку (вершину) або нескінченну множину спільних точок (сторона багатокутника). У випадку системи трьох нерівностей з трьома невідомими:

а₁₁x + a₁₂y + a₁₃z ≥ b₁

а₂₁x + a₂₂y + a₂₃z≥ b₂

………………………… (2.53)

а_i1x + a_i2y + a_i3z ≥ b₁

…………………………

а_m1x + a_m2y + a_m3z ≥ b_m

що задовольняються для одного із півпросторів, на які ділиться простір відповідною площиною (знак рівності). Областю розв'язків системи нерівностей є многогранник, який утворюється перетином півпросторів. Постійні значення лінійна функція трьох змінних L = с₁х + с₂у + c₃z приймає на перпендикулярній вектору с(с₁,с₂,с₃) площині, а екстремальні - у вершинах, на ребрах або гранях многокутника. Розглянемо застосування методу лінійного програмування стосовно розв'язання наступних задач.

Приклад. Для відгодівлі худоби використовуються грубі корма та концентрати. У 1 кг грубих кормів міститься 0,25 кормових одиниць та 0,04 кг білку, а 1 кг концентратів містить 0,8 кормових одиниць та 0,08 кг білку. Добовий раціон містить не менше 10 кормових одиниць та не менше 1,2 кг білку. Скласти добовий раціон так, щоб вартість кормів була мінімальною, якщо вартість 1 кг концентратів становить 5 грн., а грубих кормів - 2 грн.

Позначимо кількість концентратів і грубих кормів у раціоні через х і у відповідно. Із умови задачі маємо:

L = 5x + 2y, (2.54)

0,8х + 0,25у>10,

0,08х + 0,04у > 1,2, (2.55)

х >0; у >0.

Перейдемо від нерівностей до рівностей:

0,8х + 0,25у=10,

0,08х + 0,04у = 1,2, (2.56)

які являють собою рівняння прямих.

Щоб побудувати їх графіки (рис. 2.4), достатньо знайти точки перетину цих прямих з осями х та у.

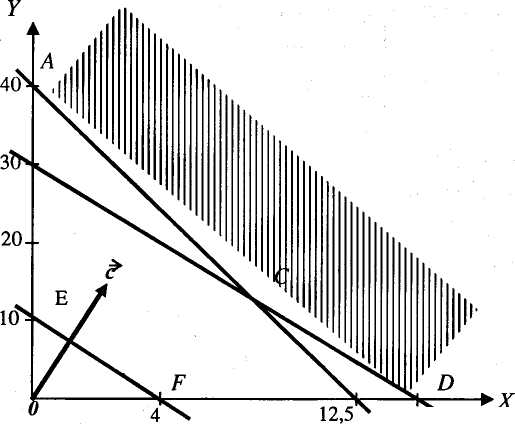
Рис. 2.4. Область визначення вартості L раціону (заштриховано)

Для першої прямої: при х=0 отримаємо у= 10/0,25=40, а при у=0 одержимо х =10/0,8=12,5.

Для другої прямої: при х=0 отримаємо у =1,2/0,04=30, а при;у=0 матимемо х =1,2/0,08=15.

Отже, область визначення лежить за межами чотирикутника OACD (заштриховано).

Побудуємо пряму (2.54) при фіксованому значенні L, наприклад, L=20: 5х+2у=20. Якщо х=0, то y=20/2=10, а при у = 0 отримаємо х =20/5=4.

За цими даними побудуємо графік прямої EF, паралельним перенесенням якої досягаємо точки С. Координатами цієї точки є точка перетину прямих (2.56). Розв'язки системи цих рівнянь методом детермінантів (визначників) дорівнюють:

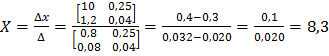(2.57)

(2.58)

Підставляючи ці значення у вираз (2.54), матимемо:

L_min= 5 - 8,3 + 2-13,3=41,5+26,6=68,1 грн.

Приклад. Фермеру за 10000 грн. треба купити не більше 100 кг грубих кормів і не більше 200 т концентратів, 1 т яких містить 300 і 800 кормових одиниць і коштує 75 і 200 грн. відповідно. Яку кількість кормів кожного типу треба купити, щоб раціон мав найбільшу кількість кормових одиниць?

Нехай через х і у позначимо вагу в тоннах грубих кормів та концентратів.

Згідно умови задачі маємо:

L = 300x + 800у,

75х + 200у < 10000,

0 < х <100, 0 < у ≤ 200

Із рівняння 75х + 200у = 10000 знайдемо точки перетину цієї прямої з осями: х = 0, у = 10000 / 200 = 50; у = 0, х = 10000 / 75 = 133.

Побудуємо графіки цієї прямої і прямої x = 100, які обмежують область (заштриховано) значень х і у (рис. 2.4). При значенні L = 10000 обчислимо точки перетину прямої 300х + 800 у = 10000 з осями: х = 0, у = 10000 / 800 = 12,5; у = 0,

х = 10000/300 ≈ 33,3. Побудуємо графік цієї прямої, паралельним переміщенням якої попадаємо у точку С. Координатами цієї точки є точка перетину прямих х = 100 і 75х + 200y = 10000: при x = 100 матимемо:

75 × 100 + 200y = 10000,

звідки:

у = (10000 - 75000) / 2000 = 12,5.

Отже. Lmах = 300 × 100 + 800 × 12,5 = 40000.

Таке саме значення приймає L у точці A(50;0): Z_max= 800 × 50 = 40000, а також у будь-якій точці прямої АС.

Приклад. Оптимізувати структуру стада ВРХ господарства, у якому загальне і маточне поголів'я не повинно перевищувати 2000 і 1200 голів відповідно, таким чином, щоб забезпечити максимум валового доходу. Прибуток від однієї корови становить 60 грн., а від однієї голови інших груп ВРХ - 40 грн.

Позначимо через х і у поголів'я маточного та інших груп ВРХ у стаді.

За умови задачі маємо:

х + y ≤ 2000,

x ≤ 1200,

х ≥ 0, у ≥ 0,

L = 60x + 40y

Знайдемо точки перетину прямої х + у = 2000 з осями координат:

у = 0, х = 2000

х = 0, у = 2000

При L = 1200 точки перетину прямої 60 x + 40y = 1200 з осями координат становлять:

у = 0, x = 1200 / 60 = 20;

х = 0, x = 1200 / 40 = 30.

Графіки прямих x + y = 2000, х = 1200, 60x + 40y = 1200 і область можливих значень змінних зображуються аналогічно попередній задачі (рис. 2.5), де треба зробити заміну: 50 Ž2000; 133Ž2000; 12,5Ž30; 33,5Ž20.

Координати точки С становитимуть:

х = 1200, у = 2000 - 1200 = 800

а максимальне значення:

Lmах = 60 × 1200 + 40 × 800 = 104000 голів..

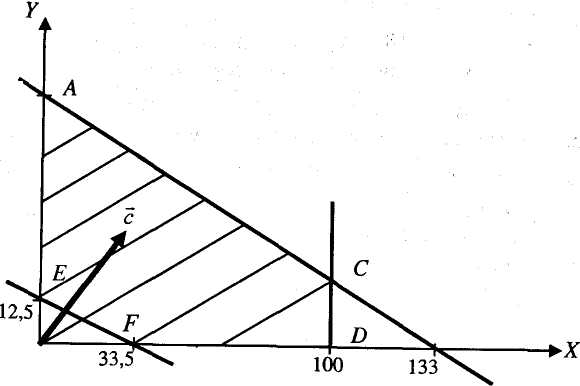
Рис. 2.5. Область визначення кількості кормових одиниць в раціоні

Приклад. Фірма виготовляє з одного виду сировини два продукти А та В, що продаються відповідно за 8 та 15 грн. за упаковку. Ринок збуту для кожного з них практично необмежений. Сировина для продукту А обробляється технологічною лінією 1, а для продукту В - технологічною лінією 2. Потім обидва продукти упаковуються на молокозаводіі. Схему виробництва продуктів А та В зображено на рис. 2.6.

Технологічна лінія 1

Автоматіз упаку-вання

Продукт А

Сировина для продукції А і В

Технологічна лінія 2  

Продукт В

Рис. 2.6. Схема виготовлення продуктів

Ціна 1 кг сировини - 6 грн. Технологічна лінія1 обробляє за годину 5т сировини, а технологічна лінія 2 - 4т сировини із втратами, що становлять відповідно 10 і 20%. Технологічна лінія1 може працювати 6год. на день, причому його використання коштує 2880 грн./год; технологічна лінія 2 – 2 -5 год. на день, що коштує 3360 грн./год.

Маса продукту А в одній упаковці дорівнює 1/4 кг, а продукту В - 1/3 кг. Фабрика може працювати 10 год. на день, щогодини упаковуючи 12 000 одиниць продукту А або 8000 одиниць продукту В. Вартість її роботи протягом 1 години становить 3600 грн.

Необхідно відшукати такі значення х ₁ та х ₂ обсягів використання сировини для виготовлення продуктів А та В (у тоннах), які забезпечують найбільший щоденний прибуток фірми.

Рішення. Нехай х ₁ та х ₂ - відповідно обсяги сировини, використовувані для виготовлення продукту А та В за один день, т.

Запишемо обмеження задачі. Згідно з умовою обмеженими ресурсами є тривалість використання технологічної лінії 1 і 2, а також тривалість роботи молокозаводу з упакування продуктів А та В.

1. Обмеження на використання технологічної лінії 1.

Зміст цього обмеження такий:

1. Фактична тривалість використання технологічної лінії 1 з обробки сировини для виготовлення продукту А має не перевищувати 6 год., тобто:

Математично це запишеться так:

х ₁ / 5 ≤6, або х ₁ ≤ 30.

2. Обмеження щодо використання технологічної лінії 2 виразимо аналогічно:

х ₂ / 4 ≤ 5, або х ₂ ≤ 20.

3. Обмеження щодо тривалості роботи фабрики з упакування продуктів А та В. Зміст цього обмеження такий: фактична кількість часу, витраченого на упакування продуктів А та В, має не перевищувати 10 год на день (2.59):

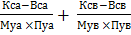≤ 10 год. (2.59)

де Кса - ;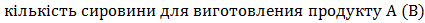

Вса - ;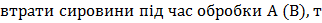

Муа – ;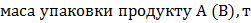

Пуа - п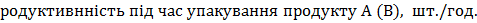

Математично це запишеться так:

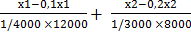≤ 10

або:

0,3 х ₁ + 0,3 х ₂ ≤ 10,

3 х ₁ + 3 х ₂ ≤ 100.

Побудуємо цільову функцію задачі. Прибуток фірми дорівнює різниці між доходом від реалізації виготовленої продукції та витратами на її виробництво.

1. Дохід від виробництва продуктів А та В (2.60):

× Ціна однієї упаковки, грн. (2.60)

або

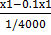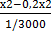8 + 15

Загальний дохід дорівнює: 2880 х ₁ + 3600 х ₂.

2. Витрати на сировину визначаємо як загальну кількість сировини в тоннах, використовуваної для виробництва продуктів А та В, помножену на вартість 1 т сировини у гривнях:

6000 (х ₁ + х ₂) = 6000 х ₁ + 6000 х ₂.

3. Витрати, пов’язані з технологічних ліній 1 і 2, визначаємо множенням фактичної тривалості роботи технологічної лінії з обробки сировини на вартість 1 години роботи відповідноїтехнологічної лінії.

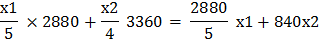
4. Витрати, пов’язані з упакуванням продуктів А та В, дорівнюють добутку фактичної тривалості роботи молокозаводу (0,3 х ₁ + 0,3 х ₂) на вартість 1 год її роботи, яка становить 3600 грн:

3600 (0,3 х ₁ + 0,3 х ₂) = 1080 х ₁ + 1080 х ₂.

Беручи до уваги всі складові цільової функції, можна записати математичний вираз прибутку фірми за день:

Z = (2880 х ₁ + 3600 х ₂) – (6000 х ₁ + 6000 х ₂) – (2880/5 х ₁ + 840 х ₂) – (1080 х ₁ + 1080 х ₂) = 12/5 × (26 х ₁ + 45 х ₂).

Отже, маємо такий остаточний запис економіко - математичної моделі:

Z max= 12/5 × (26 х ₁ + 45 х ₂) (23)

за умов:

3х₁ + 3х₂ ≤ 100 (24) 2.61

х₁ ≤ 30, (25) 2.62

х₂ ≤ 20, (26) 2.63

х₁ ≥ 0, х₂ ≥ 0 (27) 2.64

Графічне розв’язання задачі ілюструє рис. 2.7.

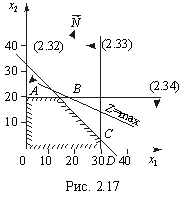
Рис. 2.7. Область визначення обсягів використання сировини для виготовлення продуктів А та В

Областю допустимих планів, що утворюється системою обмежень задачі, є багатокутник АВСDО. Найбільшого значення цільова функція досягає у вершині В. Координати цієї точки визначаються розв’язанням системи рівнянь:

3х₁ + 3х₂ = 100 х₁= 40/3;

х₁ = 20 х₂= 20.

Дата добавления: 2014-11-29