Порядковая функция на графе. Понятие уровня

Способы задания графов.

Определение графа, виды графов.

Формализация описания структур на основе теории графов.

Элементам системы ставят в соответствие вершины графа, а связям - рёбра или дуги графа.

Пусть определено некоторое множество элементов V. Граф G=G(V) считается определённым, если задано некоторое множество сочетаний элементов или пар вида E=(a, b), где a, b ÎV, указывающие, какие элементы считаются связанными. Пара E=(a, b) называется ребром, a, b – вершинами. Если порядок расположения концов безразличен, т.е. если E=(a, b)=(b, a), то говорят, что E – неориентированное ребро, если порядок важен, то говорят, что E – ориентированное ребро.

Ребро Е инцидентно (т.е связано) с вершинами a, b, и вершины a, b инцидентны ребру Е. Граф, составленный из неориентированных рёбер, называется неориентированным, а составленный из ориентированных рёбер называется ориентированным графом.

Есть смешанные графы. Неориентированный граф G может быть превращён в ориентированный при помощи процесса удвоения, состоящего в замене каждого ребра парой рёбер с теми же концами и приписывании им противоположных ориентаций.

А. Графическое представление. Достоинство – наглядность. Недостаток – не может быть использовано при решении задач структурного анализа с помощью ЭВМ.

Б. Матричное представление.

1) Матрица смежности для вершин неориентированного графа: А= 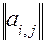, где n – число вершин в графе.

a _i,j = {1 при наличие связи; 0 при отсутствии связи

Матрица смежности для вершин ориентированного графа.

a _i,j = {1, если из вершины i можно перейти в вершину j; 0 в противном случае

2) Матрица инцидентности В= 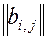i=1, 2… n j=1, 2… m, где n – число вершин, m – число рёбер;

z – для неориентированного графа:

b _i,j = {1, если i-я вершина инцидентна данному j-му ребру (есть связь); 0, если

нет связи;

для ориентированного графа:

b _i,j = {1, если i-я вершина есть начало j-го ребра; -1, если i-я вершина есть конец

j-го ребра; 0, если i-я вершина не инцидентна j-му ребру.

В. Множественное представление. В этом случае для ориентированного графа G(V) задаётся множество вершин V и соответствие G, которое показывает, как связаны между собой вершины.

Для каждой вершины i соответствие G определяет множество вершин G(i), в которые можно непосредственно попасть из вершины i. В ряде случаев G(i) называется множеством правых инциденций.

Множество (i) определяет все вершины, из которых можно попасть в вершину i, а поэтому называется обратным соответствием. (i) называется множеством левых инциденций.

Пример: Способы формализации исходной структуры системы.

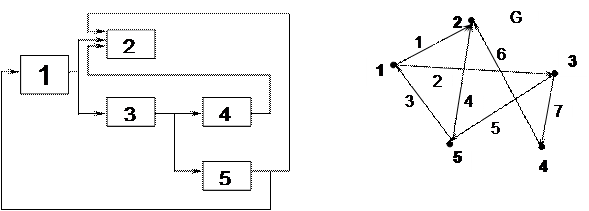Рис. 3.1 Структура системы. Рис. 3.2 Граф системы.

Матрица смежности вершин А:

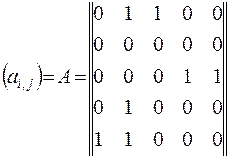
Матрица инцинденций вершин В:

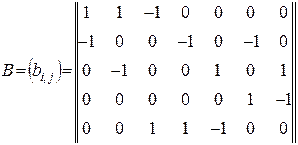
i=1,2,3,4,5 кол-во вершин, j=1,2,3… 7 кол-во рёбер. Множественное задание структуры системы сводится к системе множеств:

G(1)=(2,3) G(2)=0 G(3)=(4,5) G(4)=(2) G(5)=(1,2)

(1)=(5) (2)= (1,5,4) (3)=(1) (4)=(3) (5)=(3)

Дата добавления: 2014-11-29