Пример: уравнение Беллмана в задаче о рекламной деятельности

Непрерывный вариант динамического программирования

Метод динамического программирования разработан и для непрерывной задачи оптимального управления, в которой поведение ОУ описывается дифференциальным уравнением в векторной форме

или в скалярной форме

.

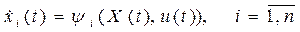Показатель качества имеет вид:

.

Начальный момент процедуры управления и начальное состояние ОУ заданы; конечный момент процедуры управления 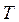задан, конечное состояние ОУ не задается, т.е. рассматривается задача с фиксированным временем и свободным правым концом траектории.

Доказательство условия оптимальности опирается на принцип оптимальности Беллмана, сформулированный в разделе 2.1, и использует вытекающую из этого принципа процедуру попятного движения.

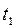Выделим произвольным образом внутри интервала два момента времени и , причем , где 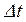- бесконечно малый промежуток времени.

Рассмотрим сначала решение задачи для интервала , примыкающего к концу интервала управления, исходя из критерия оптимальности

. (9)

Предположим, что задача решена, и получено оптимальное управление

.

Оптимальное управление зависит от текущего времени , от момента времени и от состояния объекта , которое имеет статус начального состояния ОУ в этой промежуточной задаче.

Подставим найденное оптимальное управление в показатель качества (9), который примет минимальное значение

.

Функция 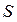получила название функции Беллмана. Она знакома нам по дискретному варианту динамического программирования и сохраняет здесь тот же физический смысл: функция Беллмана представляет собой минимальное значение показателя качества при оптимальном управлении. В задаче с фиксированным временем функция Беллмана зависит от вектора состояния 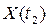и от времени , т.е. является функцией переменных.

Рассмотрим теперь решение задачи для интервала , исходя из критерия

. (10)

Предположим, что эта задача решена, и получено оптимальное управление

.

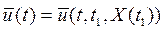Подставим это управление в показатель качества (10), который примет минимальное значение

.

Найдем связь между функциями Беллмана для моментов времен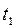и и . Возьмем за основу функцию и запишем ее в виде

.

От управляющего воздействия на интервале зависит только второе слагаемое, минимизация которого проведена на предыдущем шаге. Заменим второе слагаемое его минимальным значением :

.

Второе слагаемое остается в составе фигурных скобок, так как от управления на интервале зависит состояние объекта 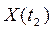. Рассмотрим первое слагаемое. Интервал времени 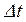, разделяющий моменты 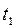и , является бесконечно малым, поэтому первое слагаемое заменим его приближенным значением:

.

В итоге

. (11)

Вектор состояния разложим в ряд Тейлора в окрестности 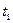и ограничим разложение линейными членами:

.

Производную вектора состояния заменим правой частью уравнения объекта . Получим

. (12)

Теперь второе слагаемое представим в виде

.

Функцию Беллмана разложим в ряд Тейлора в окрестности точки 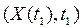и ограничим разложение линейными членами. При этом предполагается, что функция Беллмана дифференцируема по своим аргументам. Если в результате решения задачи функция Беллмана окажется дифференцируемой, то полученное решение будет справедливым. В противном случае дальнейшие рассуждения носят эвристический характер.

Используя разложение в ряд Тейлора, получим следующую связь между значениями функции Беллмана в моменты времени 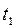и :

. (13)

Приращения , являются элементами вектора из соотношений (12), поэтому 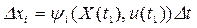, и соотношение (13) примет вид

.

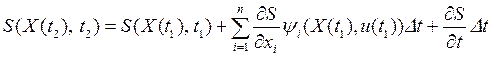Подставим этот результат в выражение (11):

.

Упростим это соотношение. Прежде всего, заметим, что величина в составе фигурных скобок не зависит от управления 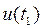, следовательно, она может быть вынесена из процедуры минимизации и взаимно уничтожена с такой же величиной из левой части. Таким же образом можно обосновать перенос в левую часть последнего слагаемого в составе фигурных скобок. Сокращаем все слагаемые на величину 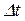, а момент времени , выбранный произвольным образом внутри интервала , заменяем текущим временем . В итоге получим уравнение Беллмана:

.

Уравнение Беллмана является инструментом решения непрерывных задач оптимального управления. Оно решается за 3 шага. На первом шаге из условия минимума выражения в фигурных скобках находится оптимальное управление .

На втором шаге оптимальное управление подставляется в уравнение Беллмана, которое рассматривается теперь как дифференциальное уравнение в частных производных относительно неизвестной функции Беллмана . Из решения этого уравнения находится функция Беллмана .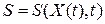

На третьем шаге функция Беллмана 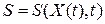подставляется в выражение для оптимального управления, найденное на первом шаге. Оптимальное управление принимает окончательный вид: 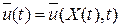и может быть использовано для построения оптимальной системы управления в виде замкнутой нестационарной системы с обратной связью по вектору состояния.

Наиболее трудоемким в этой процедуре является второй шаг, связанный с решением дифференциального уравнения в частных производных.

В задаче оптимального управления с нефиксированным временем управления 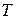уравнение Беллмана принимает более простой вид:

.

Упрощение достигается за счет того, что функция Беллмана зависит только от вектора состояния 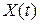и не зависит от времени, поэтому производная . К задаче с нефиксированным временем управления относится, в частности, задача оптимального управления с критерием

.

Применим уравнение Беллмана к задаче о рекламной деятельности фирмы, которая с целью увеличения объема продаж осуществляет рекламу своего товара. Исходное уравнение, связывающее объем продаж 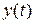с затратами на рекламу , имеет вид:

Затраты на рекламу подвержены ограничению: 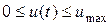. Необходимо найти рекламную политику фирмы на интервале времени 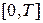, 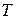задано, исходя из критерия оптимальности

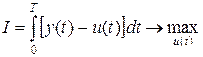. (14)

В разделе 1.2 исходное уравнение было преобразовано в дифференциальное уравнение второго порядка:

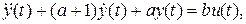
а затем с помощью переменные состояния 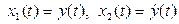представлено в виде системы двух дифференциальных уравнений первого порядка, записанных в нормальной форме Коши:

(15)

Вывод уравнения Беллмана проводился из условия минимума показателя качества; в нашем примере показатель качества требуется максимизировать. Приведем исходную задачу (14) к нужному виду с учетом новых переменных:

.

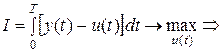
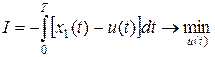Так как конечный момент времени 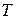задан, применяем уравнение Беллмана в общей форме:

.

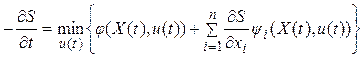В условиях данной задачи

,

и уравнение Беллмана принимает вид:

.

1 шаг. Из условия минимума выражения в фигурных скобках найдем структуру оптимального управления. Управляющее воздействие входит сюда линейным образом, поэтому классический способ оптимизации из условия

,

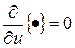к успеху не приведет. Преобразуем выражение в фигурных скобках, обобщив слагаемые, содержащие управляющее воздействие :

.

Процедуру минимизации проведем с учетом ограничения: 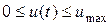на основе следующих рассуждений:

1) если 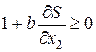, то ,

2) если , то .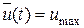

Таким образом, оптимальное управление может принимать только граничные значения в зависимости от знака функции переключения , которая в итоге является функцией времени и может несколько раз изменять знак на интервале времени 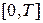. Функция переключения содержит неизвестную функцию Беллмана в виде частной производной , поэтому ни число переключений, ни моменты переключений установить невозможно. Отсутствие этой информации затрудняет решение задачи в рамках второго и третьего шагов для нахождения конкретного вида оптимального управления.

Дата добавления: 2014-11-29