Пример: принцип максимума в задаче о рекламной деятельности

Вернемся к задаче о рекламной деятельности фирмы и рассмотрим ее решение с помощью принципа максимума Понтрягина. Исходное уравнение, связывающее объем продаж 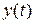с затратами на рекламу , имеет вид:

.

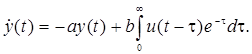
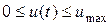Необходимо найти рекламную политику фирмы на интервале времени 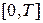, 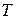-задано, исходя из критерия оптимальности

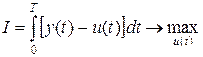. (21)

В разделе 1.2 исходное уравнение было преобразовано в дифференциальное уравнение второго порядка:

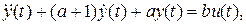(22)

а затем с помощью переменных состояния 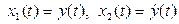представлено в виде системы двух дифференциальных уравнений первого порядка, записанных в нормальной форме Коши:

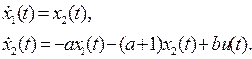
Для решения задачи потребуются начальные условия 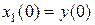и 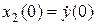. Известно, что на предыдущем этапе реклама не проводилась, поэтому начальные условия могут быть только нулевыми (см. раздел 1.2).

Вывод основных соотношений принципа максимума проводился из условия минимума показателя качества; в нашем примере показатель качества требуется максимизировать. Поэтому приведем исходную задачу (21) к нужному виду и учтем также введение переменных состояния:

.

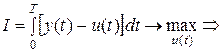
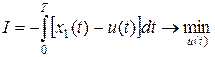Введем дополнительную переменную состояния x₀(t) в соответствии с правилами:

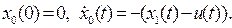
Следующим этапом является формирование функции Гамильтона

.

В условиях данного примера

.

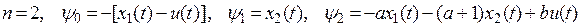Функция Гамильтона и условие оптимальности примут вид:

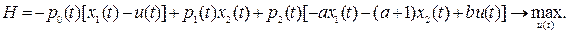
Управляющее воздействие входит в это выражение линейным образом, поэтому классический способ оптимизации, использующий условие 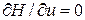, к успеху не приведет. Преобразуем гамильтониан, оставив в нем только те слагаемые, которые зависят от u(t), и представим условие оптимальности в более компактной форме:

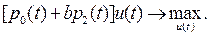
С учетом ограничения 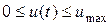получим следующую структуру оптимальных затрат на рекламу:

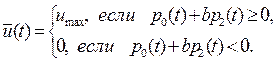
Таким образом, оптимальные затраты на рекламу лежат на границах ограничения и в определенные моменты времени переходят с одной границы на другую. Похожий результат был получен в разделе 2.6 при решении задачи методом динамического программирования на основе уравнения Беллмана. Однако там этот результат оказался окончательным; дальнейшего продвижения в решении задачи в разделе 2.6 не произошло.

Моменты переходов оптимального управления с одной границы на другую определяются функцией переключения

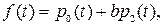
которая содержит неизвестные функции p₀(t) и p₂(t). Эти неизвестные функции в соответствии с принципом максимума находятся из системы уравнений

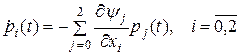. (23)

Рассмотрим первое уравнение из этой системы для :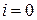

.

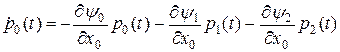Так как функции 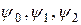не зависят от 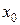, то все частные производные здесь равны нулю и уравнение принимает вид 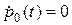. Следовательно, 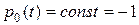, так как .

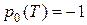Рассмотрим второе уравнение из системы (23) для :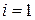

.

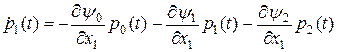Здесь частные производные 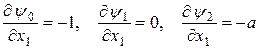, и с учетом 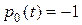второе уравнение примет вид: .

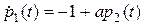Рассмотрим третье уравнение из системы (23) для :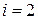

.

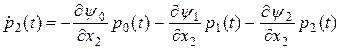Здесь частные производные 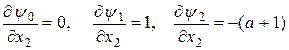, и третье уравнение примет вид .

Таким образом, для нахождения функци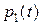й и 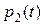нужно решить систему дифференциальных уравнений:

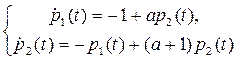
при конечных условиях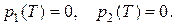

Если из первого уравнения выразить неизвестную функцию 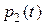и подставить ее во второе уравнение, то придем к дифференциальному уравнению

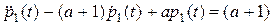. (24)

Это линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его общее решение состоит из общего решения 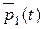соответствующего однородного уравнения и частного решения 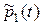неоднородного уравнения. Общее решение однородного уравнения

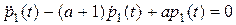
находится на основании характеристического уравнения 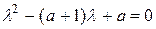с корнями 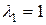, 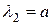. Таким образом, общее решение

,

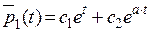где 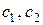- постоянные интегрирования. Частное решение найдем по виду правой части уравнения (24) и характеру корней. Корни вещественные и разные, а правая часть уравнения является константой. Поэтому частное решение нужно искать также в виде константы. В итоге частное решение

.

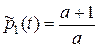Запишем решение дифференциального уравнения:

.

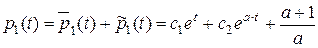Для отыскания постоянных интегрирования найдем сначала функцию

.

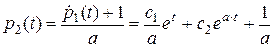На основании конечных условий для 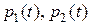составим систему уравнений

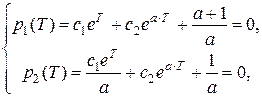
из решения которой найдем постоянные интегрирования

, .

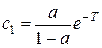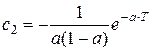В итоге найдём

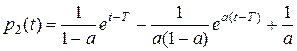
и сформируем функцию переключения

.

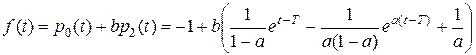Анализ функции переключения на интервале времени [0, T ] показывает, что при b>a функция переключения один раз меняет свой знак с плюса на минус. Соответственно, оптимальное управление состоит из двух участков, на первом из которых оно совпадает с верхней границей ограничения: 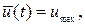а на втором участке – с нижней границей: 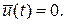Таким образом, рекламная кампания должна состоять из двух этапов. На первом этапе затраты на рекламу должны быть максимально возможными, на втором этапе рекламную деятельность следует полностью свернуть. Момент времени, разделяющий эти этапы, определяется функцией переключения и зависит от конкретных параметров задачи.

При b<a функция переключения на всем интервале [0, T ] лежит в отрицательной области, поэтому оптимальное управление 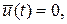т.е. рекламную деятельность проводить не следует. Чтобы дать экономическое обоснование этому результату, представим дифференциальное уравнение (22) в виде:

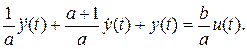
Коэффициент b/a, стоящий в правой части, можно рассматривать как коэффициент пропорциональности, связывающий объем продаж рекламируемого товара с затратами на рекламу в установившемся режиме. Если этот коэффициент больше единицы, т.е. b>a, то объем продаж превышает затраты на рекламу; рекламная деятельность имеет смысл. Если этот коэффициент меньше единицы т.е. b<a, то объем продаж не превышает затрат на рекламу; рекламная деятельность не имеет смысла.

В качестве числового примера рассмотрим задачу с параметрами а =0,2; b =1; u_max =5; Т =7. В этих условиях функция переключения примет вид:

.

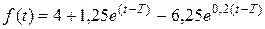Результаты решения задачи представлены на рис. 21. Верхний график характеризует поведение функции переключения f (t), которая изменяет знак с плюса на минус при 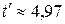. На среднем графике показано оптимальное управление (затраты на рекламу). На начальном этапе планируемого периода 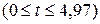на рекламу должны тратиться все выделяемые средства. На втором этапе 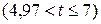рекламную кампанию необходимо свернуть. Последний график отражает изменение объема продаж у (t) рекламируемого товара.

Объём продаж 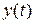найден из решения дифференциального уравнения:

.

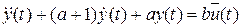Решение состоит из двух этапов. На первом этапе 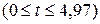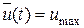, и рассматривается уравнение 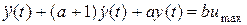при начальных условиях 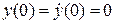. Процесс решения аналогичен решению дифференциального уравнения для 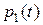, поэтому приведем окончательный результат:

, .

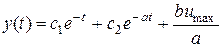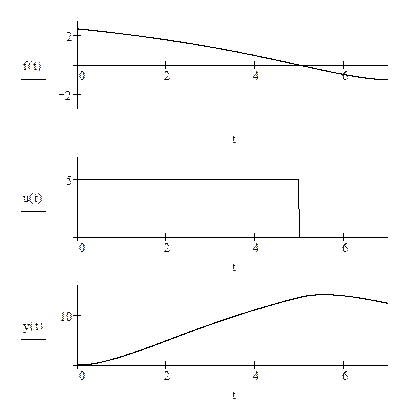
Рис. 21

Постоянные интегрирования 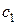и 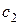найдем из начальных условий 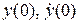, предварительно выразив :

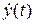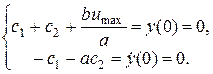
Отсюда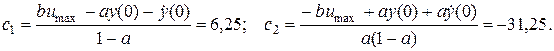

Таким образом, на первом этапе объем продаж 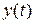описывается зависимостью

.

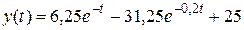В конце первого этапа при 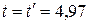продажа товара характеризуется параметрами .

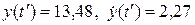На втором этапе 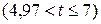рассматривается дифференциальное уравнение

,

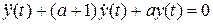решение которого имеет вид

.

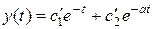Постоянные интегрирования 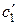и 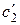находятся из конечных значений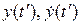

для первого участка:

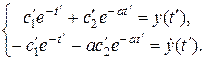
Отсюда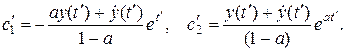

Таким образом, на втором этапе объем продаж 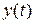описывается зависимостью

.

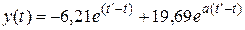В конце второго этапа 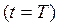продажа товара характеризуется параметрами .

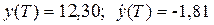В целом результаты данного примера помогают снять проблему, которую поднимает знаменитое высказывание Уильяма Левера: «Половина денег, которые идут на рекламу, выбрасывается впустую; но как узнать, какая именно половина?».

Дата добавления: 2014-11-29