Гамільтонові цикли

Задача про ланцюги

Теорія графів почалася з розв’язування задачі про кенігсберзькі мости (Ейлер, XVIII ст.). Розташування мостів в м. Кенігсберг наведено на рис.8.

Рис. 8.

В місті є 7 мостів { a, b, c, d, e, f, g }, які його розбивають на чотири частини { A, B, C, D }. Необхідно обійти всі мости міста, проходячи по кожному рівно один раз, і повернутись у початкову точку.

Граф для цієї задачі наведений на рис.9.

Рис.9.

Загальна постановка задачі є наступною (Ейлер): в яких випадках у скінченному неорієнтованому графі можна знайти такий цикл, у якому кожне ребро графу зустрічалось би рівно один раз. Якщо такий цикл існує, то він називається ейлеревим циклом, а сам граф називається ейлеревим.

Твердження. Скінченний граф G (V) є ейлеровим тоді і тільки тоді, коли:

1) G (V) - зв’язний граф;

2) локальні степені всіх його вершин парні.

Алгоритм побудови ейлеревого циклу:

1) вибираємо довільну вершину a Î V;

2) будуємо довільний ланцюг P з початком у вершині „ a ”. Оскільки локальні степені всіх вершин графу є парні, то ланцюг може завершитись тільки в „ a ” (тобто він є циклом);

3) якщо P (a, a) містить не всі ребра графу G (V), то будуємо граф G ₁ = G ‑ P (a, a), в якому всі вершини мають теж парний локальний степінь. Оскільки граф G (V) є зв’язним, то серед вершин P (a, a) має знайтись вершина „ b ”, яка зв’язана ребром хоча б з однією вершиною графу G (V) (інакше граф G був би незв’язним);

4) будуємо з ребер графу G ₁ ланцюг P ’, що починається у вершині „ b ” і може закінчуватись тільки у „ b ”; з ланцюгів P і P ’ будуємо новий цикл:

P ₁(a, a) = P (a, b) È P ’(b, b) È P (b, a);

5) якщо P ₁(a, a) не містить всіх ребер графу G (V), то, за аналогією з кроком 3) будуємо граф G ₂ = G – P ₁(a, a) і т.д.

З огляду на скінченність графу, цей процес зупинитися, коли всі ребра графу G (V) будуть вичерпані.

Узагальнюючи задачу Ейлера можна шукати найменшу кількість ланцюгів (не циклів!) P ₁, які не перетинаються по ребрах і покривають увесь зв’язний граф G (V).

Твердження. Нехай G (V) - скінченний зв’язний граф з k вершинами непарного локального степеня. Тоді мінімальна кількість ланцюгів, які не перетинаються по ребрах і покривають граф G, дорівнює k / 2.

Алгоритм побудови ланцюгів P_i.

1) з’єднуємо довільно чином пари вершин з непарним локальним степенем (для цього необхідно k / 2 ребер). При цьому утворюється граф G ₁, всі вершини якого мають парний степінь;

2) граф G ₁ є ейлеровим і в ньому існує ейлерів цикл S;

3) після відкидання з циклу S доданих на кроці 1) k / 2 ребер, отримуємо k / 2 ланцюгів, які покривають весь граф G.

Приклад

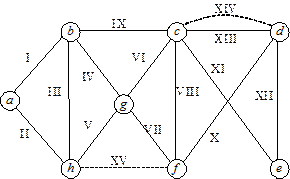
Рис. 10.

Степені вершин графу:

Вершина	a	b	c	d	e	f	g	h
Степінь

Таким чином, k = 4. З’єднаємо ребрами вершини (c, d) та (f, h) (на рис.10 ці ребра позначені штриховими лініями).

Поетапно побудуємо для утвореного графу цикл Ейлера:

а) P ₁ = (І, ІІІ, ІІ);

б) P ₂ = (І, ІХ, VI, IV, III, II);

в) P ₃ = (І, IX, XIII, XII, XI, VI, IV, III, II);

г) P ₄ = (I, IX, XIV, X, VIII, XIII, XII, XI, VI, IV, III, II);

д) P ₅ = (I, IX, XIV, X, VIII, XIII, XII, XI, VI, VII, XV, V, IV, III, II).

Віднімаючи додані раніше ребра XIV і XV, отримаємо три ланцюги:

1) (І, Х);

2) (Х, VIII, XIII, XII, XI, VI, VII);

3) (V, IV, III, II).

Зауважимо, що перший і третій ланцюги мають спільний кінець – вершину „ а ”. „Склеюючи” ці ланцюги, отримаємо остаточно:

1) (V, IV, III, II, I, IX);

2) (X, VIII, XIII, XII, XI, VI, VII).

Для орієнтованих графів має місце

Твердження. Нехай G (V) - орієнтований зв’язний граф. Граф G містить ейлерів цикл тоді і тільки тоді, коли у кожну вершину v входять стільки ж ребер, скільки і виходить:

r (v) = r *(v).

Якщо в неорієнтованому графі кожне неорієнтоване ребро замінити двома орієнтованими і протилежно направленими, то мають місце умови попереднього твердження і тому правильне таке

Твердження. У скінченному зв’язному неорієнтованому графі завжди можна побудувати орієнтований цикл, який проходить через кожне ребро по одному разу в кожному з двох напрямків.

Визначення. Гамільтонів цикл – це цикл, який проходить по кожній вершині графа і рівно один раз.

До знаходження гамільтонового циклу приводить, наприклад, задача комівояжера: деякий район містить пеану кількість міст, які повинен обійти комівояжер. Відомі відстані між всіма містами. Необхідно знайти найкоротший шлях, який проходить через всі міста і повертається в початковий пункт.

Незважаючи на подібність у формулюванні для ейлерових і гамільтонових циклів, відповідні теорії мають мало спільного. Критерій існування ейлеревих циклів був встановлений достатньо просто; для гамільтонових циклів ніякого загального правила невідомо. Більше того, для конкретних графів іноді тяжко встановити, чи існує взагалі такий цикл. Тому обмежимось одним критерієм.

Твердження. (Дірак). Якщо в графі G (V) з n вершинами для довільної вершини v Î V: r (v) ³ n / 2, то в графі існує гамільтонів цикл.

На закінчення зауважимо, що є різні задачі пошуку маршрутів у графі:

- з’ясування чи граф є ейлеревим та знаходження відповідного ейлеревого циклу

- знаходження найменшої кількості ланцюгів, які не мають спільних ребер та покривають увесь граф

- з’ясування чи граф є гамільтоновим

- знаходження маршрут, що зв’язує дві довільні задані вершини

- знайти найкоротший шлях з однієї заданої вершини в іншу задану вершину (зокрема для зважених графів)

Дата добавления: 2014-11-29