Введение 4 страница

Однако определение силы удара 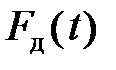по формуле (8.1) весьма затруднительно, так как неизвестно время соударения, т. е. время, в течение которого скорость движущегося тела снижается от своего максимального значения в момент соприкосновения с ударяемым телом (начало удара) до нуля после деформации последнего (конец удара). В связи с указанными трудностями, определяя напряжения в элементах упругих систем, вызываемые действием ударных нагрузок (динамические напряжения), в инженерной практике обычно пользуются так называемым энергетическим методом, основанным на законе сохранения энергии. Согласно этому методу полагают, что при соударении движущихся тел уменьшение запаса кинетической энергии их равно увеличению потенциальной энергии деформации соударяющихся упругих тел.

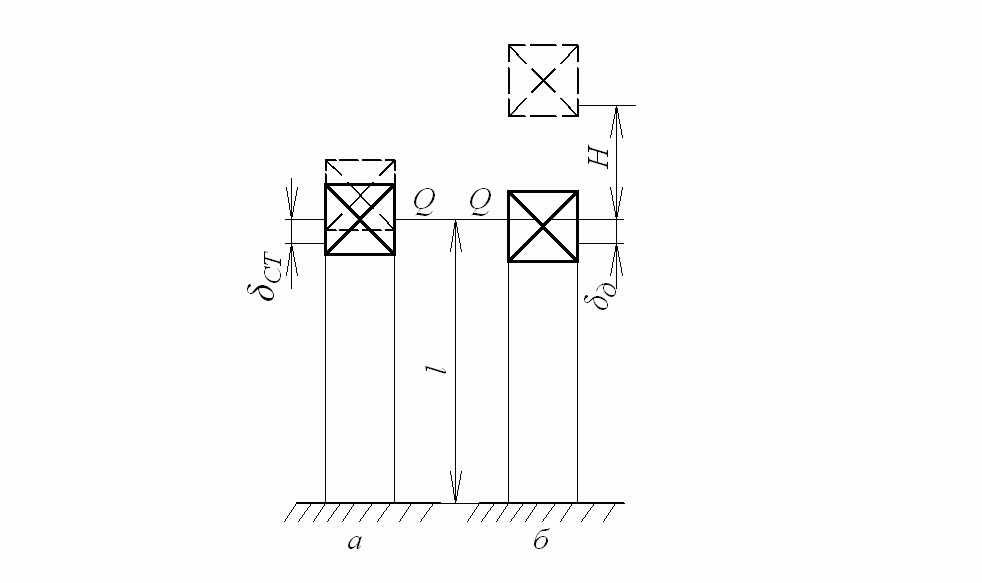
Вывод расчетных формул для определения динамических напряжений проведем на примере простейшей системы (рис. 8.1), состоящей из вертикально расположенного упругого призматического стержня с жесткостью 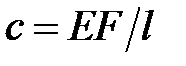и некоторого груза Q. Полагаем при этом, что удар неупругий в том смысле, что при соударении падающий груз не отскакивает от стержня, а движется вместе с ним, и, следовательно, в стержне не возникают упругие волны. Кроме того, данная система обладает одной степенью свободы.

Рассмотрим два случая:

1) груз Q прикладывается к стержню статически, т. е. нагрузка медленно нарастает от нуля до своего максимального значения (рис. 8.1,а) и сжимает стержень на величину ;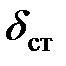

2) груз падает с некоторой высоты H и, ударяя по стержню, создает в нем сжатие 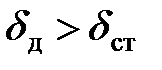(рис. 8.1,б).

а	б

Рис. 8.1. Статическая нагрузка и нагрузка ударом

Изменение деформации при ударном действии нагрузки Q по сравнению с деформацией при статическом приложении той же нагрузки может быть охарактеризовано коэффициентом динамичности

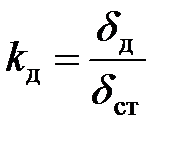
(8.2)

откуда динамическую деформацию через статическую можно выразить формулой

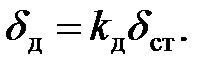
(8.3)

Учитывая линейную связь между напряжением и деформацией, а также принимая одинаковыми модули упругости при статическом и ударном действии нагрузки, что с достаточной степенью точности подтверждается экспериментом, по аналогии с последней формулой можно установить связь между статическим и динамическим напряжениями:

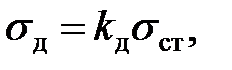
(8.4)

где

—

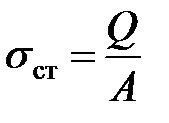(8.5)

напряжение, возникающее в стержне при сжатии силой, равной весу падающего груза.

Чтобы использовать формулу (16.4), нужно определить коэффициент динамичности 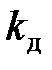. При этом будем исходить из общепринятого в теории удара допущения, что связь между усилиями и деформациями сохраняется одной и той же как при статической, так и при динамической нагрузках, т. е.

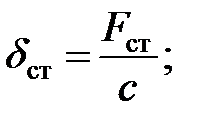
	(8.6)
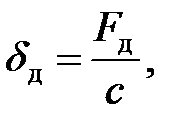
	(8.7)

где 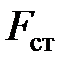— статическая нагрузка, равная весу падающего груза (в нашем случае — );

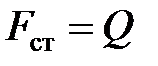— динамическая нагрузка, представляющая собой силу инерции ударяющего тела в первый момент его соприкосновения со стержнем.

Изменение кинетической энергии падающего груза численно равно работе, совершенной им при падении и деформировании стержня:

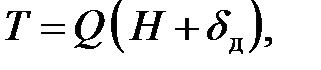
(8.8)

а потенциальную энергию деформации упругого тела при ударе, накопленную за счет уменьшения потенциальной энергии падающего тела, учитывая выражение (16.7), устанавливающее связь между усилием и деформацией, можно представить формулой

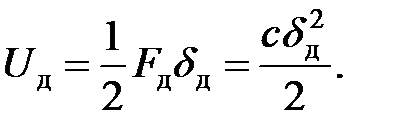
(8.9)

Пользуясь законом сохранения энергии и пренебрегая потерями энергии, вызываемыми местными пластическими деформациями при соударении тел, а также инерцией массы ударяемого стержня, можно записать

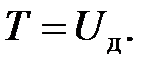
На основании выражений (8.8) и (8.9)

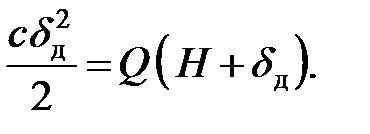
(8.10)

Имея в виду, что 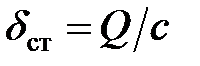, уравнение (8.10) можно представить так:

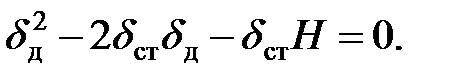
Отсюда можно определить динамическую деформацию:

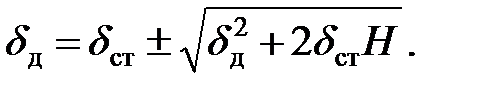
(8.11)

Поскольку знак «минус» в этой формуле не соответствует физической стороне рассматриваемой задачи, следует сохранить знак «плюс».

Записав формулу (16.11) в виде

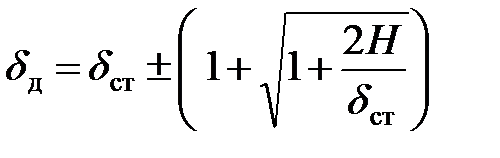
(8.12)

и сопоставив ее с формулой (8.3), находим выражение для коэффициента динамичности:

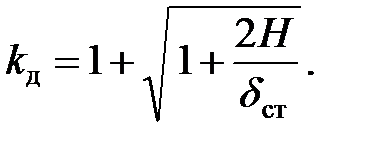
(8.13)

Имея в виду, что 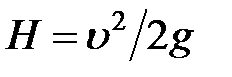( 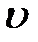— скорость падающего груза в начале удара), коэффициент динамичности можно представить формулой

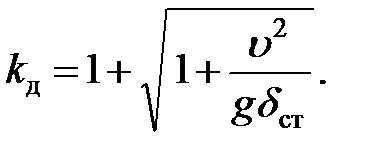
(8.14)

Если учесть, что

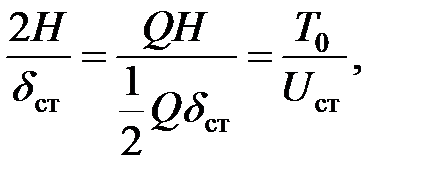
то коэффициент динамичности 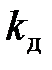можно также записать и так:

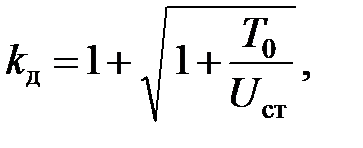
(8.15)

где 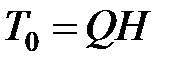— кинетическая энергия падающего груза к моменту соударения;

— потенциальная энергия деформации подвергающегося удару упругого стержня, которая накапливается в нем при статическом действии силы, равной весу ударяющего груза Q, т. е.

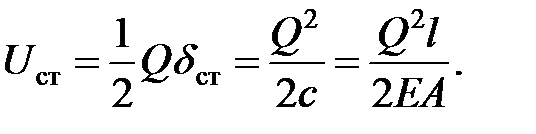
(8.16)

Если 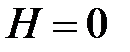, т. е. сила прикладывается внезапно, то, согласно выражению (16.13), коэффициент динамичности 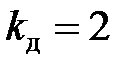. Поскольку высота падения груза H всегда значительно больше 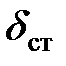, то в большинстве случаев определения коэффициента динамичности в выражениях под корнем единицей по сравнению со вторым слагаемым можно пренебречь. Тогда на основании выражения (8.13) получим:

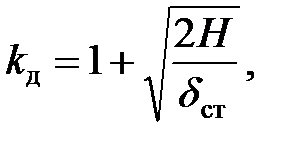
(8.17)

или, согласно формуле (8.15),

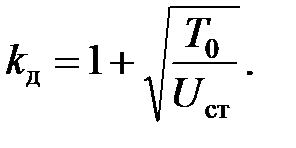
(8.18)

Имея выражение (8.13) для коэффициента динамичности, напряжение при ударе на основании зависимости (8.4) определим формулой

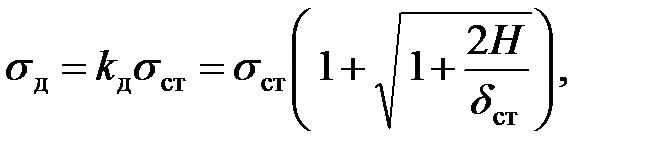
(8.19)

или

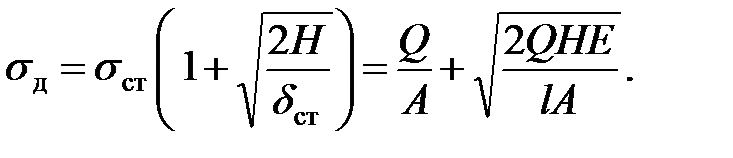
(8.20)

Аналогично определяем и усилие при ударе:

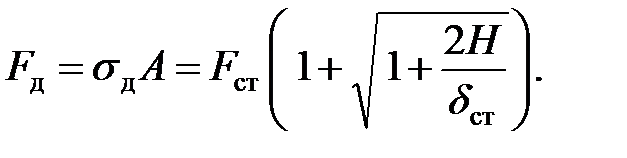
(8.21)

Изложенная приближенная теория расчета на удар имеет определенные пределы применения. Они обусловлены скоростью падающего груза к моменту удара и жесткостью конструкции, что выражается в формулах (8.13) или (8.15) отношением 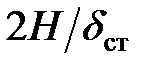или 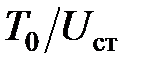. Так, если

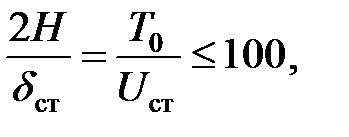
то ошибка расчета не превышает 10 %. Учет массы ударяемой конструкции расширяет пределы применения приближенной теории.

Из анализа формул (8.19) и (8.20) видно, что при равномерно распределенных напряжениях, одинаковых во всех сечениях стержня, величина динамических напряжений зависит не только от площади A его поперечного сечения, как это имеет место в случае действия статической нагрузки в статически определимых системах, но и от длины l и модуля упругости E материала стержня, т. е. можно сказать, что динамические напряжения в стержне при ударе зависят как от объема, так и от качества его материала. При этом, чем больше объем упругого стержня, подвергающегося удару (чем больше «энергоемкость» стержня), тем меньше динамические напряжения, возникающие в нем, а чем больше модуль упругости материала стержня, тем динамические напряжения больше.

До сих пор предполагалось, что стержни по всей длине имеют одинаковые сечения. Именно для таких стержней справедливо все сказанное о роли объема стержня при оценке динамических напряжений.

Картина оказывается несколько иной в стержнях, отдельные участки которых имеют различную площадь поперечного сечения. В этом случае (рис. 8.2, а) наибольшее номинальное напряжение в стержне (без учета концентрации) будет в месте наименьшей площади (в месте выточки). Зависит оно, как известно, от деформативности всего стержня, а не только его ослабленной части. Понизить динамические напряжения в этом случае можно двумя путями: увеличением поперечного сечения в месте выточки или уменьшением площади поперечного сечения утолщенной части стержня и, следовательно, повышением податливости всего стержня в целом, что приводит к снижению максимальных динамических напряжений в месте выточки. Если изготовить весь стержень постоянного диаметра, равного диаметру выточки 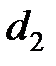, то при этом существенно увеличится деформативность стержня, а, следовательно, уменьшится динамическое напряжение .

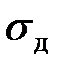Таким образом, снижение напряжений при ударе может быть достигнуто увеличением объема путем уничтожения выточки, т. е. выравниванием напряжений по различным сечениям, или уменьшением объема материала за счет уменьшения площади утолщенной части, что приводит к увеличению деформативности.

Сказанное удобно проиллюстрировать на примере определения максимальных динамических напряжений, возникающих в трех типах стержней при продольном ударе грузом Q, падающим с одной и той же высоты H.

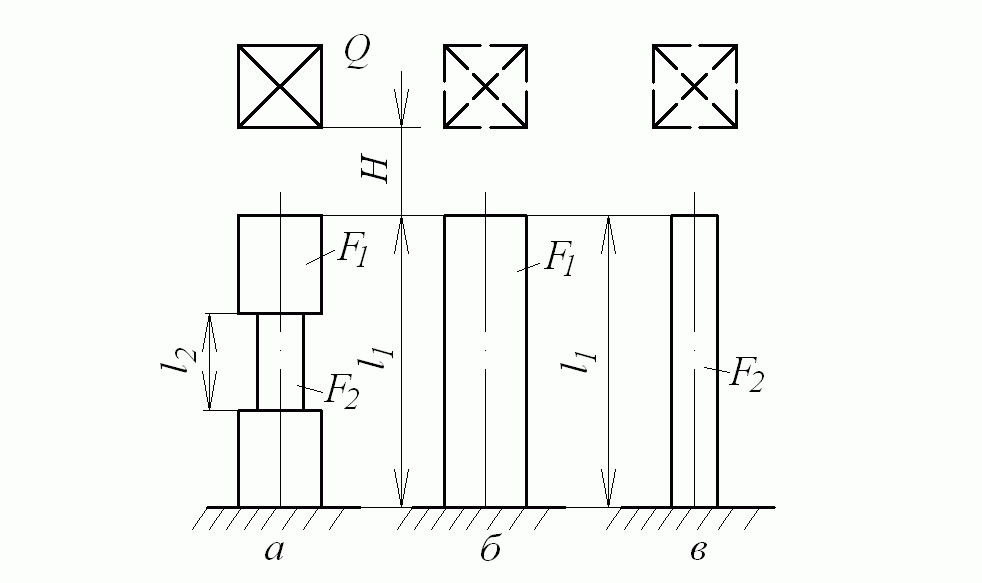
а	б	в

Рис. 8.2. К определению напряжений в трех типах стержней при ударе

Пусть соотношения между отдельными размерами стержней следующие:

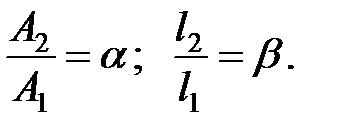
Для определения напряжений в каждом из стержней воспользуемся общей формулой

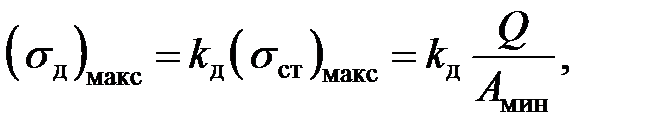
где

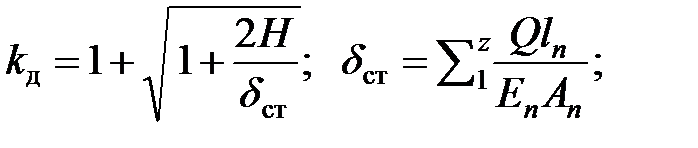
n — число ступеней.

Для ступенчатого стержня (рис. 16.2, а)

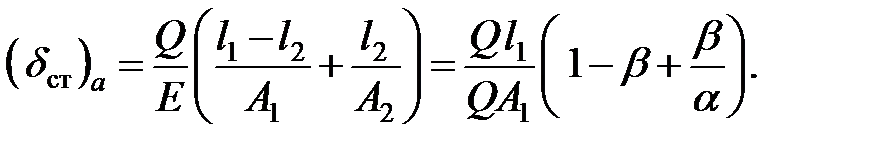
Для стержня постоянного сечения с размерами утолщенной части ступенчатого стержня (рис. 8.2, б)

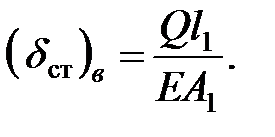
Для стержня постоянного сечения, равного минимальному сечению ступенчатого стержня (рис. 8.2, в), имеем

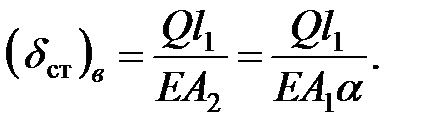
Тогда соотношения между деформациями отдельных стержней, очевидно, будут следующими:

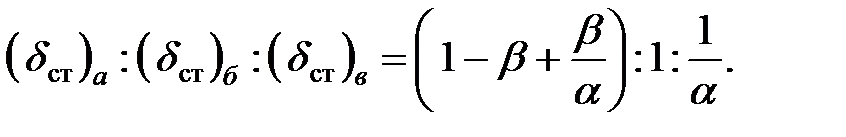
(8.22)

Пренебрегая в выражении (8.17) единицей по сравнению с корнем, что при большой высоте падения H и малой статической деформации 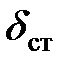можно допустить, выражение для коэффициента динамичности приближенно можно записать в виде

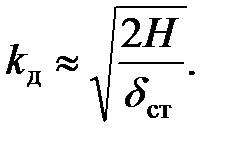
Пользуясь этой формулой и учитывая выражения (8.22), получим соотношения между коэффициентами динамичности для рассматриваемых случаев:

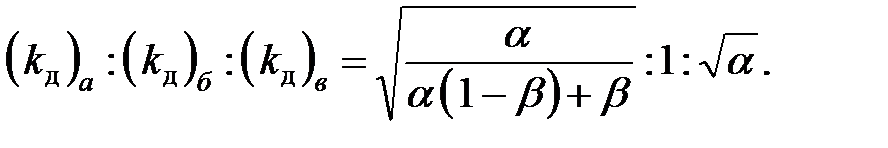
(8.23)

Исходя из выражений

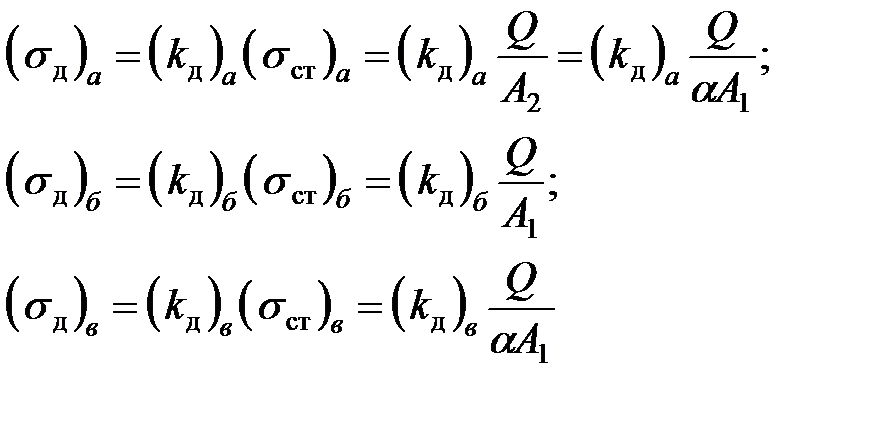
и учитывая соотношение (16.23), получим

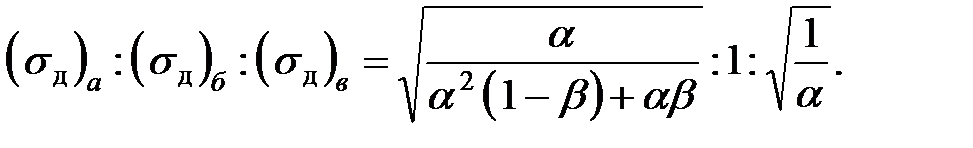
(8.24)

Предположим, например, что коэффициенты имеют следующие числовые значения:

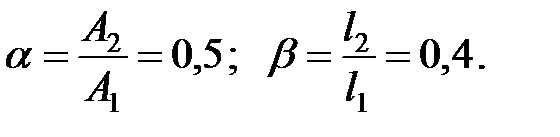
Тогда по формуле (16.24) найдем следующее соотношение:

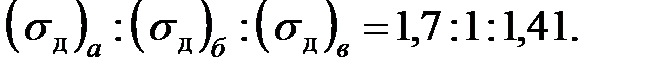
Таким образом, видим, что наибольшее напряжение возникает в стержне с выточкой (рис. 8.2,а), а наименьшее — в стержне постоянного максимального сечения (рис. 8.2,б). В стержне же минимального сечения, постоянного по длине (рис. 8.2,в), напряжение имеет некоторое промежуточное значение.

Результаты проведенного анализа имеют существенное практическое значение. Прежде всего, этот анализ показывает, что характер сопротивления стержней удару качественно резко отличается от сопротивления их статической нагрузке. При статическом сжатии утолщение одной части стержня не вызывает изменения напряжений в сечениях другой части; при ударе оно повышает их. Местное уменьшение площади поперечного сечения на небольшой длине стержня резко повышает напряжение.

Для снижения напряжений надо стремиться главным образом к увеличению податливости стержня путем увеличения его длины, добавления буферной пружины, замены материала другим, с более низким модулем упругости, выравнивания площадей поперечного сечения с целью получить все участки стержня одинаковой минимальной площади сечения. Вот почему, конструируя стержни, работающие на удар, надо добиваться постоянной площади сечения по всей их длине. Местные утолщения допустимы лишь на небольших участках длины; местные выточки небольшой протяженности крайне нежелательны. Если при таких условиях сконструировать достаточно прочный стержень не удается, необходимо удлинить его или равномерно увеличить его площадь.

Условие прочности при ударе имеет вид

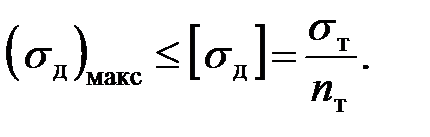
Величину коэффициента запаса 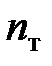можно было бы выбрать равной величине основного коэффициента запаса при статическом действии нагрузки (1,4—1,6), так как динамичность уже отражена в расчетных формулах коэффициентом 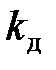. Однако ввиду некоторой упрощенности изложенного метода расчета этот коэффициент принимают несколько большим .

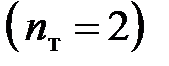Мы рассмотрели расчёт динамических напряжений в случае ударного сжатия. Однако все приведенные формулы будут также справедливы и для ударного растяжения, в частности для случая, показанного на рис. 8.3.

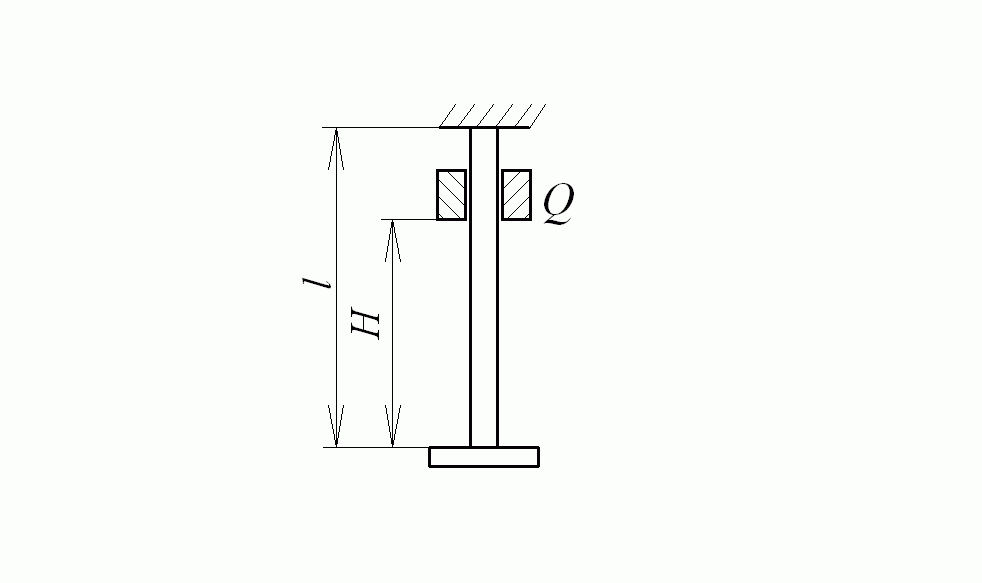
Рис. 8.3. Ударное растяжение

Пример 8.1. Груз Q весом 50 Н, прикрепленный к стальной проволоке диаметром 3 мм (рис. 8.4), свободно падает от точки А с ускорением g. Найти напряжение в проволоке, когда ее верхний конец внезапно остановлен. Массой проволоки пренебречь.

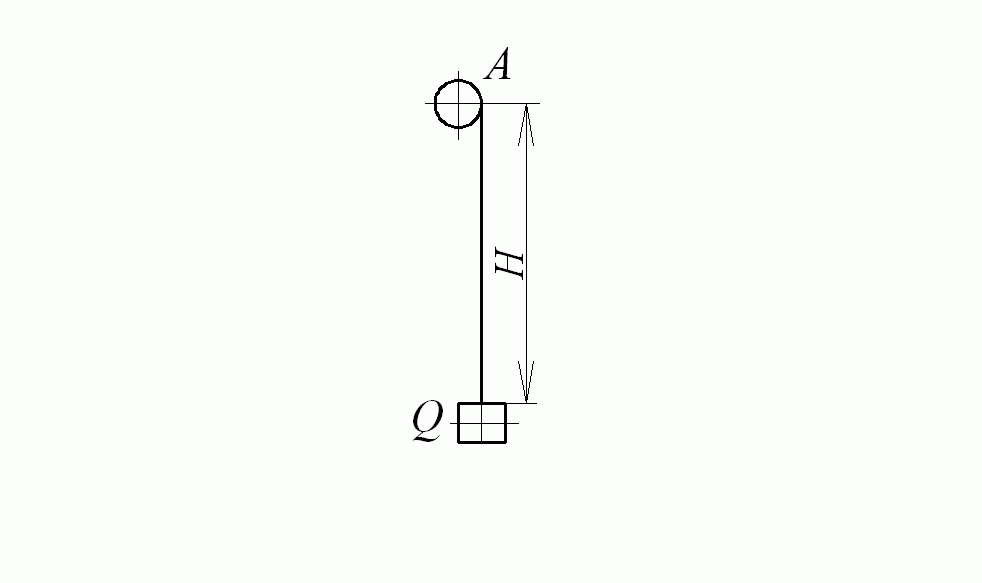
Рис. 8.4. К примеру 8.1

Решение.

Напряжение в точке A после внезапной остановки проволоки получим по формуле (8.20) при длине проволоки :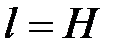

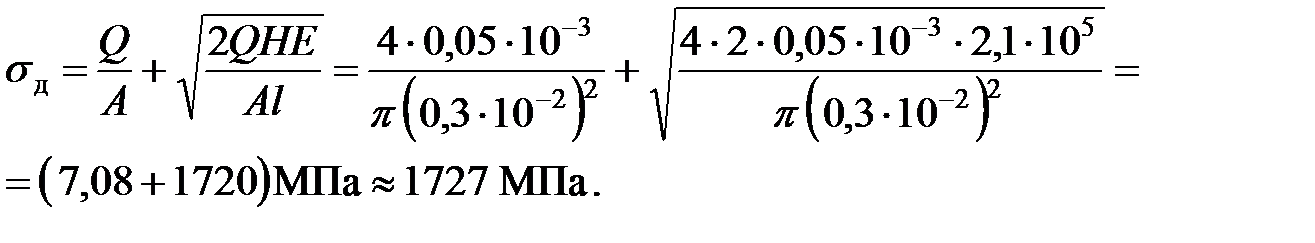
Так как кинетическая энергия падающего тела увеличивается в той пропорции, что и объем проволоки, то напряжение не зависит от высоты падения груза Q.

Пример 8.2.Определить величину динамических напряжений, возникающих в стержнях подвески (рис. 8.5) при падении груза Q = 0,25 кН с высоты H = 1 см. Площадь поперечного сечения медных наклонных стержней AC и BC 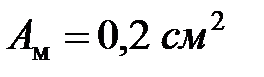, площадь поперечного сечения стального стержня 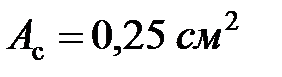, длина стального стержня 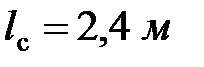; длина наклонных стержней .

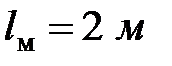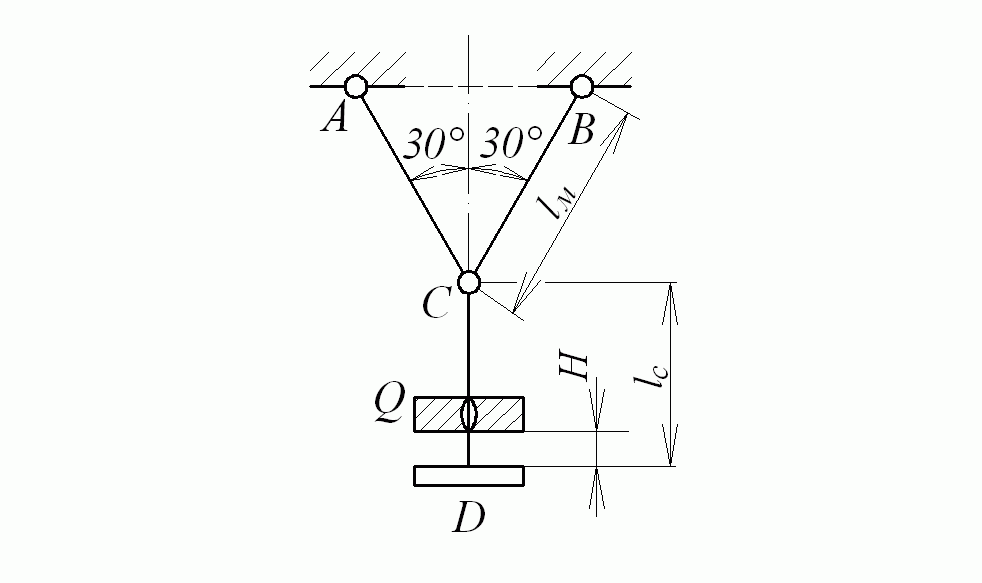
Рис. 8.5. К примеру 8.2

Решение.

Динамические напряжения в стальном стержне определяются по формуле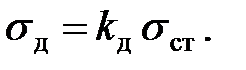

Находим значения величин, входящих в эту формулу:

Напряжения в стержнях

8.2. Расчет на удар при осевом действии нагрузки

На практике встречаются такие случаи, когда на основании полученных формул динамические напряжения найти нельзя. К числу таких задач может быть отнесена, например, задача об определении напряжений в стальном канате, поднимающем груз Q со скоростью 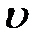при внезапном торможении подъемника (рис. 8.6).

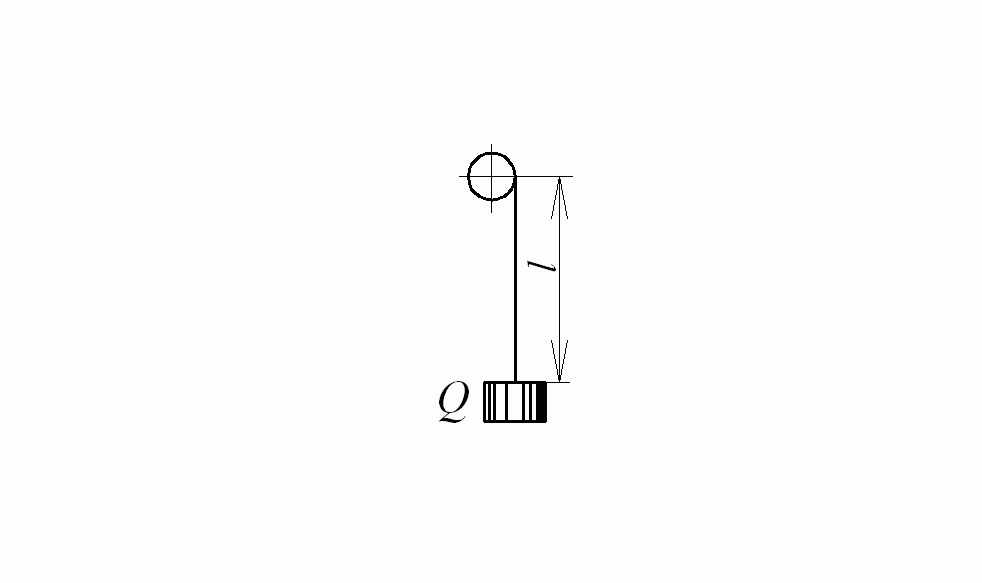
Рис. 8.6. Определение напряжений в стальном канате

Обозначим свободную длину каната в момент остановки через l и площадь поперечного сечения его через A.

Пренебрегая массой троса и полагая на основе закона сохранения энергии, что кинетическая энергия движущегося груза полностью превращается в потенциальную энергию деформации троса, получим следующее уравнение для определения наибольшего удлинения 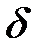троса:

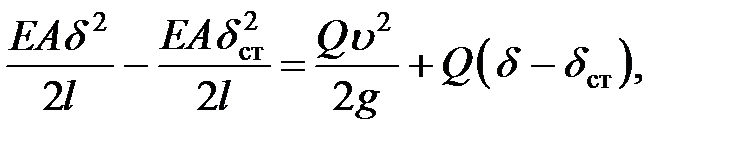
откуда, имея в виду, что

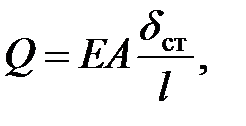
получим

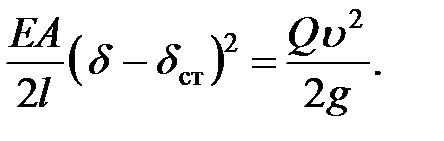
Отсюда

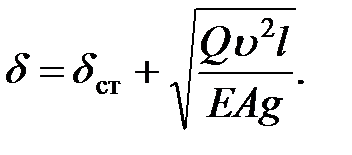
Следовательно, при внезапной остановке растягивающие напря­жения возрастают в отношении

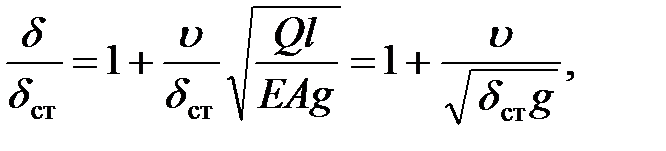
(16.25)

т.е.

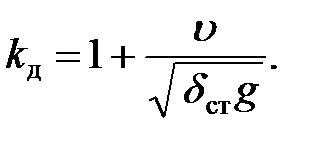
Пример 8.3.Определить напряжение в стольном канате, опускающем груз весом 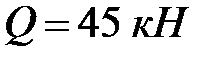со скоростью 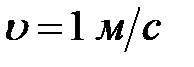в случае внезапной остановки в момент, когда груз опустится на 18 м. Сечение каната 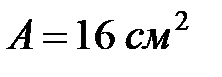, модуль упругости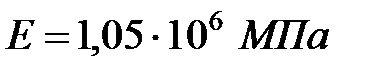

Решение.

Вычислим статическую деформацию каната:

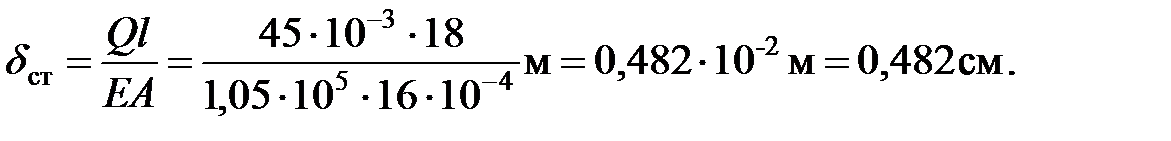
Согласно формуле (16.25), коэффициент динамичности

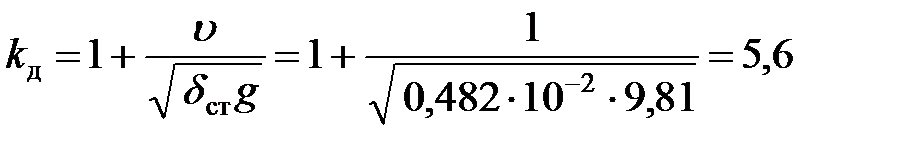
и динамические напряжения

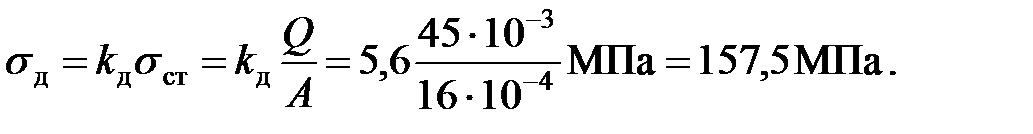
Получившиеся высокие напряжения при резком торможении могут привести к обрыву подъемного каната, что необходимо учитывать.

Пример 8.4.Решить предыдущую задачу при условии, что между тросом и грузом помещена пружина, которая под действием груза 45 кН дает статическое удлинение 12 см.

Решение.

Статическая деформация упругого элемента (каната 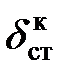и пружины )

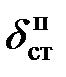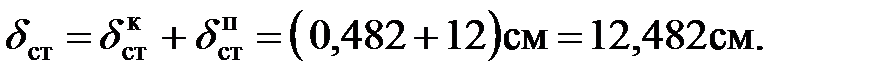
Подставляя значение 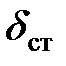в формулу (8.25), найдем, что

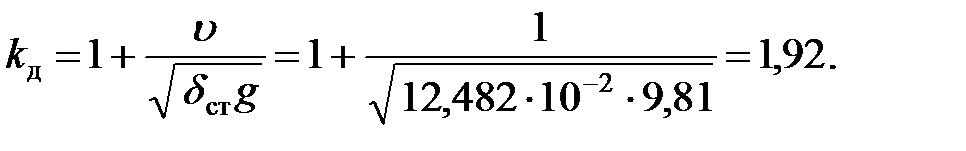
Динамическое напряжение в канате

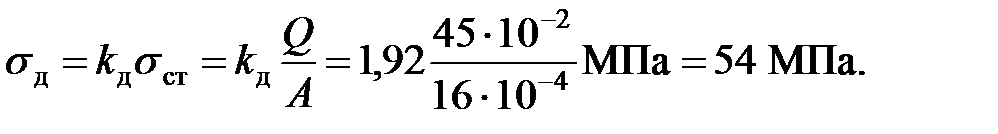
Как видим, включение пружины между канатом и грузом существенно (почти в 3 раза) снизило динамические напряжения при резком торможении груза. В данном случае пружина явилась тем амортизатором, который часто применяют в технике для смягчения толчков, а, следовательно, и уменьшения возникающих при толчках динамических напряжений.

8.3. Учет массы стержня, испытывающего удар

В некоторых случаях масса стержня может оказать существенное влияние на динамические напряжения, возникающие в стержне, подверженном действию ударных нагрузок.

Для учета влияния инерции массы ударяемого стержня в процессе удара следует различать два этапа. Первый начинается с момента соприкосновения падающего груза, имеющего максимальную скорость 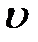, со стержнем и заканчивается, когда произойдет смятие материала, за счет чего скорость груза снизится до величины 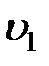, а верхний конец ударяемого тела приобретет за это время ту скорость 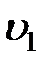. Второй этап начинается с момента совместного движения груза и конца подвергаемого удару стержня.

Если в момент начала второго этапа удара верхний конец ударяемого стержня будет иметь скорость 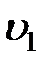, то, предположив, что скорость последующих (нижележащих) сечений стержня уменьшается по линейному закону, достигая нулевого значения в нижнем сечении стержня, найдем скорость движения произвольного сечения стержня на расстоянии x от нижнего сечения (рис. 8.7) в этот момент:

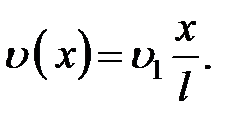
Кинетическая энергия массы участка dx, находящегося на расстоянии x от нижнего конца,

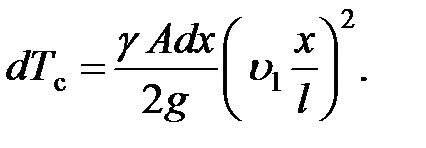
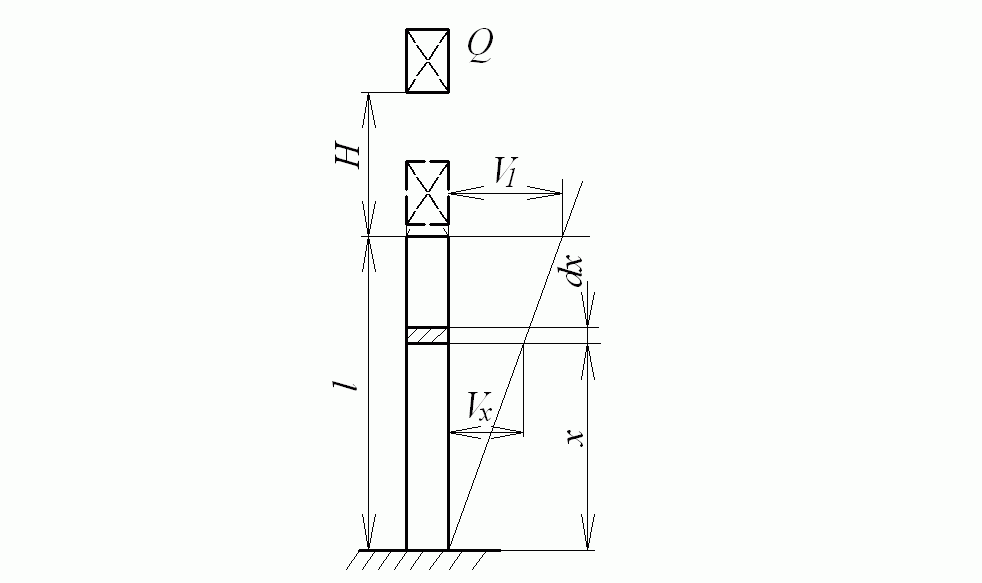
Рис. 8.7. Учет массы при ударе

Тогда полная кинетическая энергия всего стержня определится выражением

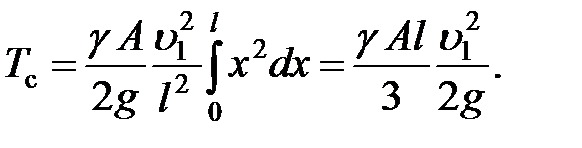
Обозначив собственный вес стержня через 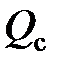, кинетическую энергию в начальный момент второго этапа можем выразить формулой

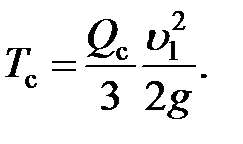
(8.26)

Таким образом, если в момент начала первого этапа удара падающий груз обладал кинетической энергией 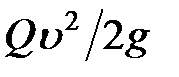, то потеря энергии до начала второго этапа за счет местных пластических деформаций

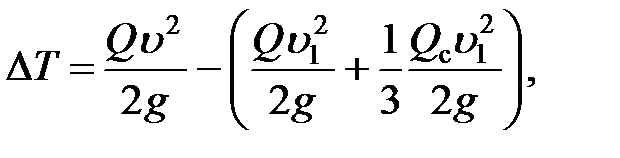
или

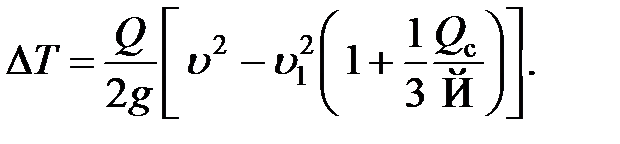
(8.27)

С другой стороны, эту же потерю кинетической энергии можно выразить, исходя из того, что скорость груза в первый этап удара изменяется на величину 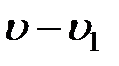, вследствие чего кинетическая энергия падающего груза уменьшается на величину 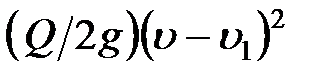. Ударяемый стержень за первый этап удара получит запас кинетической энергии 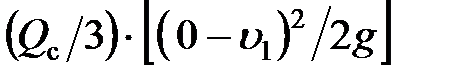. Тогда суммарная потеря кинетической энергии падающего груза, выраженная через величину потери энергии груза и запасенной энергии стержня,

или

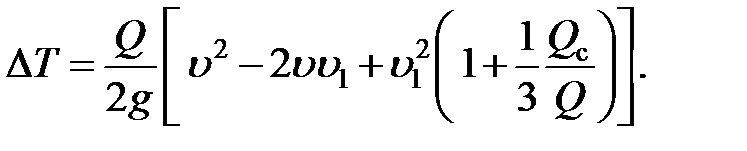
(8.28)

Приравняв правые части выражений (16.27) и (16.28) будем иметь

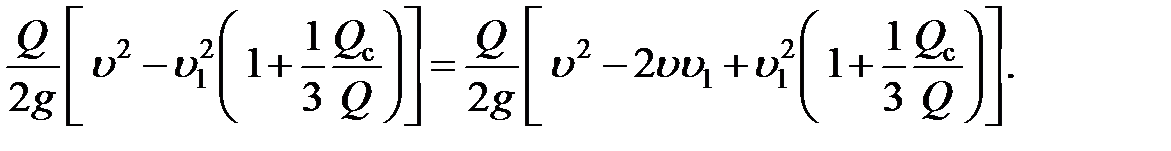
Отсюда определим величину скорости груза в момент начала второго этапа удара:

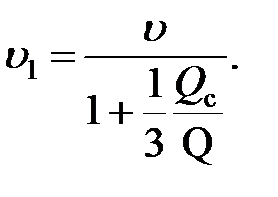
(8.29)

Энергия удара стержня, характеризуемая кинетической энергией, запасенной системой в начальный момент второго этапа удара, определится формулой

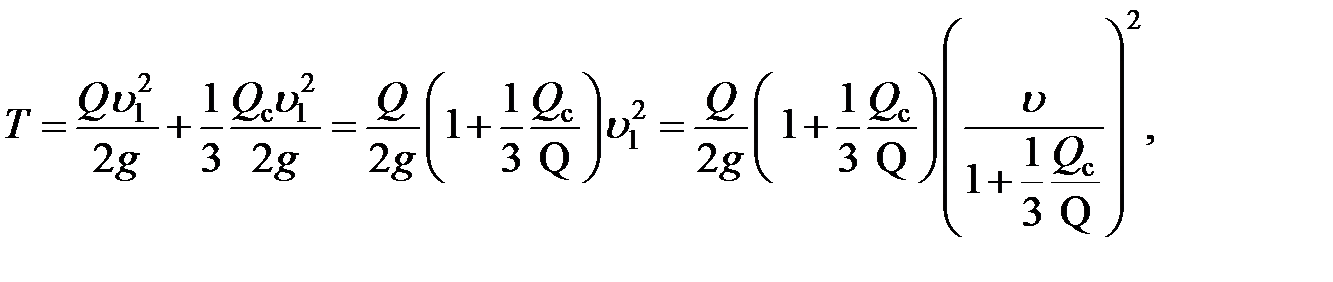
Дата добавления: 2014-12-07