Краткие теоретические сведения и основные

Задачи

1. Найти положение уровня Ферми в собственном германии при 300 К, если известно, что ширина его запрещенной зоны DW = 0,665 эВ, а эффективные массы плотности состояний для дырок валентной зоны и для электронов зоны проводимости соответственно равны: m_v = 0.388m₀; m_c = 0.55m₀, где m₀ – масса свободного электрона.

2. Уровень Ферми в полупроводнике находится на 0,3 эВ ниже дна зоны проводимости. Какова вероятность того, что при комнатной температуре энергетические уровни, расположенные на 3kT выше зоны проводимости, заняты электронами?

3. Какова вероятность того, что на уровне, расположенном у потолка валентной зоны, содержатся дырки, если ширина запрещенной зоны полупроводника 1,1 эВ (уровень Ферми расположен на 0,3 эВ ниже дна зоны проводимости)?

4. Для примесного полупроводника определить вероятность заполнения электронами энергетического уровня, расположенного на 10 kT выше уровня Ферми. Как изменится вероятность заполнения этого уровня электронами, если температуру увеличить в два раза?

5. Уровень Ферми примесного полупроводника находится на 0,01 эВ выше потолка валентной зоны. Рассчитать: а) вероятность появления дырки на верхнем уровне валентной зоны при 300 и при 50 К; б) вероятность нахождения электрона на дне зоны проводимости при 300 К при ширине запрещенной зоны полупроводника 0,67 эВ.

6. Определить, на сколько различаются вероятности заполнения электронами нижнего уровня зоны проводимости в собственном германии и собственном кремнии: а) при 300 К; б) при 100 К. Ширина запрещенной зоны при температурах 0 К и 300 К составляет соответственно 0,746 эВ и 0,665 эВ для германия и 1,165 эВ и 1,12 эВ для кремния; характер зависимости ширины запрещенной зоны от температуры считать линейной.

7. Вычислить собственную концентрацию носителей заряда в кремнии при Т = 300 К, если ширина его запрещенной зоны DW = 1,12 эВ, а эффективные массы плотности состояний m_c = 1,05m₀, m_v = 0,56m₀.

8. Концентрация электронов проводимости в полупроводнике равна 10¹⁸ м^-3. Определить концентрацию дырок в этом полупроводнике, если известно, что собственная концентрация носителей заряда при этой же температуре равна 10¹⁶ м^-3.

9. Уровень Ферми в кремнии при 300 К расположен на 0,2 эВ ниже дна зоны проводимости. Рассчитать равновесную концентрацию электронов и дырок в этом полупроводнике. Для расчета использовать данные задачи 7.

10. Уровень Ферми в германии при 300 К расположен на 0,1 эВ выше потолка валентной зоны. Рассчитать равновесные концентрации электронов и дырок в этом материале, используя данные задачи 1.

11. В собственном германии ширина запрещенной зоны при температуре 300 К равна 0,665 эВ. На сколько надо повысить температуру, чтобы число электронов в зоне проводимости увеличилось в два раза? Температурным изменением эффективной плотности состояний для дырок и электронов пренебречь.

12. Определить удельное сопротивление полупроводника n-типа, если концентрация электронов проводимости в нем равна 10²² м^-3, а их подвижность m_n = 0,5 м²/(В*с).

13. Оценить среднее время и длину свободного пробега носителей заряда при температуре Т = 300 К, если их подвижность m = 0,1 м²/(В*с), а эффективная масса m^* = 0,26m₀.

14. При напряженности электрического поля 100 В/м плотность тока через полупроводник составляет 6*10⁴ А/м². Определить концентрацию электронов проводимости в полупроводнике, если их подвижность m_n = 0,375 м²/(В*с). Дырочной составляющей тока пренебречь.

15. Вычислить отношение полного тока через полупроводник к току, обусловленному дырочной составляющей: а) в собственном германии; б) в германии р-типа с удельным сопротивлением 0,05 Ом*м. Принять собственную концентрацию носителей заряда при комнатной температуре n_i = 2.1*10¹⁹ м^-3, подвижность электронов m_n = 0,39 м²/(В*с), подвижность дырок m_p = 0,19 м²/(В*с).

16. Определить собственную удельную проводимость германия при комнатной температуре, используя значения концентрации и подвижностей носителей заряда из условия предыдущей задачи.

17. Вычислить удельное сопротивление германия р-типа с концентрацией дырок 4*10¹⁹ м^-3. Найти отношение электронной проводимости к дырочной. Собственную концентрацию и подвижность носителей заряда взять такими же, как в задаче 15.

18. При температуре Т = 300 К концентрация дырок в германии р-типа равна 2,1*10²⁰ м^-3, а конценитрация электронов в 100 раз меньше. Подвижность дырок и электронов взять из условия задачи 15. Найти собственное удельное сопротивление германия.

19. Через пластину кремния с удельным сопротивлением 0,01 Ом*м проходит электрический ток плотностью 10 мА/мм². средние скорости дрейфа электронов и дырок, если их подвижности 0,14 и 0,05 м²/(В*с) соответственно.

20. Рассчитать концентрацию электронов и дырок в германии р-типа с удельным сопротивлением 0,05 Ом*м при температуре 300 К. Недостающие данные взять из условия задачи 15.

21. Полупроводник легирован акцепторной примесью до концентрации N_a = 2n_i. Определить, во сколько раз измиенится удельная проводимость полупроводника по отношению к собственной, если отношение подвижностей электронов и дырок m_n/ m_м = b. Считается, что все акцепторы находятся в ионизированном состоянии.

22. Решить предыдущую задачу для антимонида индия, концентрация акцепторных примесей которого N_a = 5n_i. Отношение подвижности электронов к подвижности дырок равно 50.

23. Прямоугольный образец полупроводника n-типа с размерами а = 50 мм, b = 5 мм и d = 1 мм помещен в магнитное поле с индукцией В = 0,5 Тл. Вектор магнитной индукции перпендикулярен плоскости образца. Под действием напряжения U_a = 0,42 В, приложенного вдоль образца, по нему протекает ток I_a = 20 мА. Измерения показывают ЭДС Холла U_H = 6,25 мВ. Найти удельную проводимость, подвижность и концентрацию носителей заряда для этого полупроводника, полагая, что электропроводность обусловлена носителями только одного знака.

24. Образец арсенида галлия с удельным сопротивлением 5*10^-4 Ом*м характеризуется коэффициентом Холла 3*10^-4 м³/Кл. Определить: а) напряженность поля Холла, возникающего при пропускании через образце тока плотностью 10 мА/мм² и воздействии магнитного поля с индукцией 2 Тл; б) напряженность внешнего электрического поля для создания заданной плотности тока.

25. При перепаде температур DЕ = 3 К по толщине кремниевой пластины n-типа между плоскостями образца возникает термо-э.д.с. DU_t = 2,5 мВ. Определить концентрацию доноров в материале, если средняя температура образца Т = 500 К.

26. Обратный ток насыщения I_S германиевого p – n – перехода равен 0,5 мкА. Какое напряжение U надо приложить к этому переходу в прямом направлении, чтобы при температуре Т = 293 К через p – n – переход протекал прямой ток I значением 100 мА? Начертить вольт-амперную характеристику p – n – перехода.

27. Вычислить длину свободного пробега электронов в меди при Т = 300 К, если ее удельное сопротивление при этой температуре равно 0,017 мкОм*м.

28. Удельное сопротивление серебра при комнатной температуре равно 0,015 мкОм*м, а температурный коэффициент удельного сопротивления составляет 4,1*10^-3 К^-1. Определить, как и во сколько раз изменится длина свободного пробега электронов при нагревании проводника от 300 до 1000 К.

29. В медном проводнике под действием электрического поля проходит электрический ток плотностью 1 А/мм². Определить скорость дрейфа и ее отношение к средней суммарной скорости движения электронов при температуре 300 К.

30. При включении в электрическую цепь проводника диаметром 0,5 мм и длиной 43 мм разность потенциалов на концах проводника составила 2,4 В при токе 2 А. Определить удельное сопротивление материала проводника.

31. Определить время, в течение которого электрон пройдет расстояние 1 км по медному проводу, если удельное сопротивление меди 0,017 мкОм*м, а разность потенциалов на концах проводника U = 220 В. За какое время электрон пролетит это же расстояние, двигаясь без соударений, при той же разности потенциалов? Каково время передачи сигнала?

32. Вычислить удельное сопротивление металлического проводника, имеющего плотность 970 кг/м³ и молярную массу 0,023 кг/моль, если известно, что средняя скорость дрейфа электронов в электрическом поле напряженностью 0,1 В/м составляет 5*10^-4 м/с (при этом полагается, что на каждый атом кристаллической решетки приходится один электрон).

33. В металлическом проводнике с площадью поперечного сечения 0,01 мм² и сопротивлением 10 Ом концентрация свободных электронов равна 8,5*10²⁸ м^-3. Определить среднюю скорость дрейфа электронов при напряжении 0,1 В.

34. К медной проволоке длиной 6 м и диаметром 0,56 мм приложено напряжение 0,1 В. Сколько электронов пройдет через поперечное сечение проводника за 10 с, если удельное сопротивление меди равно 0,017 мкОм*м?

35. Стержень из графита соединен последовательно с медным стержнем такого же сечения. Определить, при каком отношении длин стержней сопротивление этой композиции не зависит от температуры. Удельные сопротивления меди и графита равны соответственно 0,017 и 8,0 мкОм*м, а значения a_r для этих материалов составляют 4,3*10^-3 и –10^-3 К^-1.

36. Определить температурный коэффициент линейного расширения a_l и удлинение нихромовой проволоки, если известно, что при повышении температуры от 20 до 1000⁰С электрическое сопротивление проволоки изменяется от 50 до 56,6 Ом. Длина проволоки в холодном состоянии l = 50 м. Температурный коэффициент удельного сопротивления нихрома a_r = 15*10^-5 К^-1.

37. При нагревании провода из манганина длиной 1,5 м и диаметром 0,1 мм от 20 до 100⁰С его сопротивление уменьшается на 0,07 Ом, а длина возрастает на 0,16%. Определить температурный коэффициент удельного сопротивления. При комнатной температуре удельное сопротивление манганина r = 0,47 мкОм*м.

38. Пользуясь законом Видемана-Франца-Лоренца, определить отношение удельных теплопроводностей серебра и олова при температурах 20 и 200⁰С. При температуре 20⁰С удельные сопротивления серебра и олова равны соответственно 0,015 и 0,113 мкОм*м, а температурные коэффициенты удельного сопротивления составляют соответственно 4,1*10^-3 и 4,5*10^-3 К^-1.

39. К графитовому стержню длиной 0,2 м приложено напряжение 6 В. Определить плотность тока в стержне в первый момент после подачи напряжения, если удельное сопротивление графита равно 4*10^-4 Ом*м. Как и почему меняется плотность тока в стержне со временем?

40. Вычислить удельную теплопроводность меди при комнатной температуре по измеренному значению ее удельного сопротивления r = 0,017 мкОм*м.

41. Определить внутреннюю контактную разность потенциалов, возникающую при соприкосновении двух металлов с концентрацией свободных электронов n₁ = 5*10²⁸ м^-3 и n₂ = 1*10²⁹ м^-3.

42. Определить напряженность электрического поля, возникающего в зазоре между пластинами плоского конденсатора, одна из которых изготовлена из алюминия, а другая из платины. Пластины соединены между собой медным проводом, а длина зазора l = 5 мм. Работа выхода электронов из алюминия, меди и платины составляет соответственно 4,25; 4,4 и 5,32 эВ. Как изменится напряженность поля, если пластины будут выполнены из алюминия и меди, а закорачивающий провод – из платины (при той же длине зазора)?

43. Ток в цепи, состоящей из термопары сопротивлением 5 Ом и гальванометра сопротивлением 8 Ом, равен 0,5 мА в случае, когда спай термопары помещен в сосуд с кипящей водой. Чему равна удельная термо-э.д.с. термопары, если температура окружающей среды 20⁰С?

44. Один спай термопары помещен в печь с температурой 200⁰С, другой находится при температуре 20⁰С. Вольтметр показывает при этом значение термо-э.д.с. 1,8 мВ. Чему будет равна термо-э.д.с., если второй спай термопары поместить в сосуд: а) с тающим льдом; б) с кипящей водой? Относительную удельную термо-э.д.с. во всем температурном диапазоне 0¸200⁰С считать постоянной.

45. В замкнутую цепь, состоящую из медного, алюминиевого и платинового проводников, включен милливольтметр (рисунок 13). Какую термо-э.д.с. покажет прибор при температуре спаев, указанной на рисунке, если абсолютная удельная термо-э.д.с. составляет для меди a_Cu = 1.8 мкВ/К, алюминия a_Al = -1,3 мкВ/К, платины a_Pt = -5,1 мкВ/К. Определить удельную термо-э.д.с. алюминия относительно меди и платины.

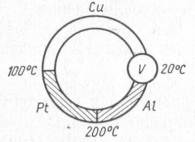
Рисунок 13

46. Из никелевой ленты шириной 1 см и толщиной 1 мм необходимо изготовить шунт сопротивлением 0,4 Ом. Какой длины должна быть никелевая лента, если удельное сопротивлением никеля 0,068 мкОм*м?

47. В цепь включены последовательно медный и нихромовый провода равной длины и диаметра. Найти отношение количеств теплоты, выделяющейся в этих проводах, и отношение падений напряжений на них. Удельное сопротивление меди и нихрома равно соответственно 0,017 и 1 мкОм*м.

48. Сопротивление провода из константана при 20⁰С равно 500 Ом. Определить сопротивление этого провода при 450⁰С, если при 20⁰С температурный коэффициент удельного сопротивления константана a_r = -15*10^-6 К^-1, а температурный коэффициент линейного расширения составляет a_l = 10^-5 К^-1.

49. Сопротивление вольфрамовой нити электрической лампочки при 20⁰С равно 35 Ом. Определить температуру нити лампочки, если известно, что при ее включении в сеть напряжением 220 В в установившемся режиме по нити проходит ток 0,6 А. Температурный коэффициент удельного сопротивления вольфрама при 20⁰С равен 5*10^-3 К^-1, температурным коэффициентом линейного удлинения можно пренебречь.

50. Определить длину нихромовой проволоки диаметром 0,5 мм, используемой для изготовления нагревательного элемента с сопротивлением 20 Ом при температуре 1000⁰С, если при 20⁰С параметры нихрома составляют: r = 1,0 мкОм*м; a_r = 1,5*10^-4 К^-1; a_l = 1,5*10^-5 К^-1.

51. Вычислить падение напряжения на полностью включенном реостате, изготовленном из константановой проволоки длиной 10 м при плотности тока 5 А/мм². Удельное сопротивление константана 0,5 мкОм*м.

52. Углеродистый резистор и проволочный резистор, изготовленный из нихрома, имеют одинаковое номинальное сопротивление R_ном = 100 Ом. Резисторы соединены параллельно и включены под напряжение U = 50 В. Одинаковая ли мощность будет выделяться на этих резисторах в процессе работы?

53. Нормально вектору напряженности однородного электрического поля Е₀ = 100 В/м расположена пластина изотропного диэлектрика с диэлектрической проницаемостью ε = 2. Определить: напряженность поля Е и электрическое смещение (электрическую индукцию) D внутри пластины; поляризованность диэлектрика Р и поверхностную плотность связанных зарядов σ.

54. Нормально вектору напряженности однородного электрического поля Е₀ расположена пластина изотропного диэлектрика с диэлектрической проницаемостью ε. Напряженность поля внутри пластины Е = 75 В/м, поверхностная плотность связанных зарядов σ = 3,32*10^-10 Кл/м². Определите значение диэлектрической проницаемости ε и напряженность внешнего электрического поля.

55. Вычислить поляризованность монокристалла каменной соли, считая, что смещение ионов под действием электрического поля от положения равновесия составляет 1% расстояния между ближайшими соседними ионами. Элементарная ячейка кристалла имеет форму куба, расстояние между соседними ионами а = 0,28 нм.

56. Определить напряженность электрического поля, действующего на монокристалл каменной соли, если ее диэлектрическая проницаемость ε = 5,65. Смещение ионов под действием электрического поля от положения равновесия составляет 1,5% расстояния между ближайшими соседними ионами. Элементарная ячейка кристалла имеет форму куба, расстояние между соседними ионами а = 0,28 нм.

57. Между обкладками плоского конденсатора без воздушных промежутков зажат лист гетинакса толщиной h = 1 мм. На конденсатор подано напряжение U = 200 В. Диэлектрическая проницаемость гетинакса ε = 6. Определите поверхностную плотность заряда на обкладках конденсатора σ и на диэлектрике σ_Д.

58. Композиционный керамический материал изготовлен на основе двух диэлектриков с диэлектрическими проницаемостями ε₁ = 40 и ε₂ = 80. Предполагая хаотическое распределение компонентов, определить состав термокомпенсированной керамики, если температурные коэффициенты диэлектрических проницаемостей равны соответственно α_ε1 = 2*10^-4 К^-1, α_ε2 = -1,5*10^-3 К^-1. Че­му равна диэлектрическая проницаемость композиционного диэлектрика?

59. Две противоположные грани куба с ребрами a = 10 мм из диэлек­трического материала с удельным объемным сопротивлением ρ_v = 10¹⁰ Ом *м и удельным поверхностным сопротивлением ρ_s = 10¹¹ Ом покрыты метал­лическими электродами. Определить ток, протекающий через эти грани куба при постоянном напряжении U₀ = 2 кВ.

60. Цилиндрический стержень диаметром 10 мм и длиной 20 мм из диэлектрика с удельным объемным сопротивлением 10¹³ Ом*м и удельным поверхностным сопротивлением 10¹⁴ Ом покрыт с торцов металлическими электродами. Чему равно сопротивление между электродами?

61. Пленочный конденсатор из поликарбоната с диэлектрической проницаемостью ε = 3 теряет за время 30 мин половину сообщенного ему заряда. Полагая, что утечка заряда происходит только через пленку диэлектрика, определить его удельное сопротивление.

62. Пленочный конденсатор из поликарбоната с диэлектрической
проницаемостью ε = 3 имеет удельное сопротивление 8,2*10¹³ Ом. Полагая, что утечка заряда происходит только через пленку ди-
электрика, определить, за какое время он потеряет 20% сообщенного ему заряда.

63. Диэлектрик в форме прямоугольного параллелепипе­да длиной l = 5 см и площадью поперечного сечения b x h = 2 x 0,5 см² с торцов покрыт ме­таллическими электродами. При напряжении U₀ = 1500 В через ди­электрик проходит ток I₀ = 10^-9 А. Найти удельное поверхностное со­противление диэлектрика, если его удельное объемное сопротивление ρ_v=10¹⁰ Ом*м.

64. Диэлектрик в форме прямоугольного параллелепипе­да длиной l = 5 см и площадью поперечного сечения bxh= 2 x 0,5 см² с торцов покрыт ме­таллическими электродами. При напряжении U₀ = 1500 В через ди­электрик проходит ток I₀ = 10^-9 А. Найти удельное объемное со­противление диэлектрика, если его удельное поверхностное сопротивление ρ_S = 2.14*10¹² Ом*м.

65. На поверхности диэлектрика параллельно друг другу расположены два ножевых электрода Расстояние между электродами b = 2 мм, их ширина h = 10 мм. Чему равно удельное поверх­ностное сопротивление диэлектрика, если сопротивление между электродами 5 МОм?

66. Спонтанная поляризованность монокристаллов титаната бария при комнатной температуре равна 0,25 Кл*м^-2. Предполагая, что причиной возникновения спонтанной поляризации является только смещение иона титана из центра элементарной кубической ячейки, определить это смеще­ние. Период идентичности α решетки принять равным 0,4 мм.

67. Пленка поливинилхлорида при электрическом пробое разрушается при напряжении 1,5 кВ. Определить толщину пленки, если ее электрическая прочность равна 50 МВ/м.

68. При каком максимальном напряжении может рабо­тать слюдяной конденсатор емкостью С =1000 пФ с площадью обкладок S = 6*10^-4 м², если он должен иметь четырехкратный запас по электрической прочности. Диэлектрическая проницае­мость слюды ε = 7, ее электрическая прочность Е_ПР =100 МВ/м. Какова толщина h слюдяной пластинки?

69. Определить запас по электрической прочности пло­ского конденсатора и толщину диэлектрика из неорганического стёкла, если емкость конденсатора 68 пФ, площадь обкладки 10 см², рабочее напряжение 10 кВ. Диэлектрическую проницае­мость стекла принять равной 6,5, а его электрическую проч­ность равной 5*10⁷ В/м.

70. В плоском конденсаторе емкостью С = 39 пФ исполь­зуется неорганическое стекло, имеющее диэлектрическую прони­цаемость ε = 6 и пробивную напряженность Е_Пр = 100 МВ/м. Какими следует выбрать толщину диэлектрика h и площадь обкладок S, если конденсатор должен работать при напряже­нии 16 кВ при четырехкратном запасе по электрической проч­ности? Возможность поверхностного пробоя при расчете не учитывать.

71. Известно, что при тепловом пробое в равномерном поле диэлектрик однородной структуры толщиной 2 мм, рас­положенный между электродами площадью 2 см², пробивается при напряжении 15 кВ. При каком напряжении пробьется этот же диэлектрик, если его расположить между электродами площадью 3 см²?

72. Известно, что при тепловом пробое диэлектрик тол­щиной 4 мм пробивается при напряжении 15 кВ на частоте 100 Гц. При каком напряжении промышленной частоты про­бьется такой же диэлектрик толщиной 2 мм?

73. Известно, что при тепловом пробое диэлектрик тол­щиной 4 мм пробивается при напряжении 15 кВ на частоте 100 Гц. Какую толщину должен иметь этот диэлектрик, чтобы пробиваться при этом же напряжении на промышленной частоте?

74. Между плоскими электродами площадью S = 2*10^-4 м² размещены соединенные последовательно две пластины из различных диэлектрических материалов. Один из них имеет диэлектрическую проницаемость ε₁ = 2, удельную проводимость γ₁ = 10^-6 Ом^-1 * м^-1 и толщину h₁ = 1 см, а другой - ε₂ = 3, γ₂ = 10^-10 Ом^-1*м^-1 и h₂ = 2 см. В момент времени t = 0 к электродам подключается постоянное напряжение U = 5 кВ. Определить напряженность электрического поля в обоих диэлектриках в моменты времени t = 0 и t → ∞. Найти напряженность электрического поля в этих диэлектриках при t → ∞, если к электродам приложено переменное напряжение U = 20 В частотой f = 50 МГц.

75. Кубик из диэлектрика с ребром 0,06 м имеет удельное объемное сопротивление 10¹² Ом*м и удельное поверхностное сопротивление 5*10¹² Ом. На противоположные грани кубика нанесены электроды, к которым при­ложено напряжение частотой 1 МГц. Определить модуль комплексной проводимости кубика на этой частоте, если его диэлектрическая прони­цаемость ε = 60.

76. Определить запас по электрической прочности пло­ского конденсатора и толщину диэлектрика из кварцевого стекла, если емкость конденсатора 80 пФ, площадь обкладки 10 см², рабочее напряжение 8,5 кВ. Диэлектрическая проницае­мость стекла 4,0, а его электрическую проч­ность - 40 МВ/м.

77. В плоском конденсаторе емкостью С = 53 пФ исполь­зуется щелочное стекло, имеющее диэлектрическую прони­цаемость ε = 5 и пробивную напряженность Е_Пр = 100 МВ/м. Какими следует выбрать толщину диэлектрика h и площадь обкладок S, если конденсатор должен работать при напряже­нии 30 кВ при четырехкратном запасе по электрической проч­ности? Возможность поверхностного пробоя при расчете не учитывать.

78. Определить запас по электрической прочности пло­ского конденсатора и толщину диэлектрика из неорганического стёкла, если емкость конденсатора 68 пФ, площадь обкладки 10 см², рабочее напряжение 10 кВ. Диэлектрическую проницае­мость стекла принять равной 6,5, а его электрическую проч­ность равной 5*10⁷ В/м.

Дата добавления: 2014-12-07