Распределения) по относительной частоте

Оценка вероятности (биноминального

Пусть производятся независимые испытания с неизвестной вероятностью р появления события А в каждом испытании. Требуется оценить неизвестную вероятность р по относительной частоте, т.е. надо найти ее точечную и интервальную оценки.

Точечная оценка. В качестве точечной оценки неизвестной вероятности р принимают относительную частоту , где m – число появлений события А, n – число испытаний.

Эта оценка несмещенная, т.е. ее математическое ожидание равно оцениваемой вероятности.

Действительно, учитывая, что М(m) = np, получаем:

М(W) = М(m/n) = = = p.

Дисперсия оценки равна D(m) = npq. Тогда получаем: D(W)= D = = = = = .

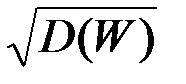Интервальная оценка. Найдем доверительный интервал для оценки вероятности по относительной частоте. Воспользуемся формулой:

= 2Ф , (1)

где Х – нормальная случайная величина с математическим ожиданием М(Х) = 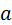. Если n достаточно велико и вероятность р не очень близка к нулю и к единице, то можно считать, что относительная частота распределена приближенно нормально, причем (как было указано выше), М (W) = p.

Тогда, с помощью формулы (1), получаем:

= 2Ф (2).

(2) – приближенное равенство, т.к. относительная частота распределена приближенно нормально.

Пусть равенство (2) выполняется с надежностью :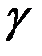

= 2Ф = .

Тогда получаем:

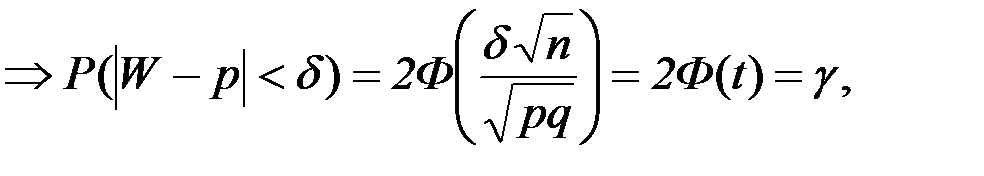
Заменим случайную величину W неслучайной наблюдаемой относительной частотой и подставим (1-р) вместо q. Тогда с надежностью выполняется неравенство:

.

Так как р неизвестна, решим это неравенство относительно р. Пусть . Обе части этого неравенства положительны. Возведя их в квадрат, получим равносильное квадратное неравенство относительно р:

D > 0 корни различны и действительны.

Меньший корень равен

(3)

Больший корень равен

(4)

Итак, искомый доверительный интервал 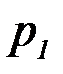< p < , где и находят по формулам (3) и (4).

При выводе мы предположили, что , тот же результат получим и при .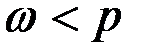

Пример: Производят независимые испытания с одинаковой, но неизвестной вероятностью р появления события А в каждом испытании. Найти доверительный интервал для оценки вероятности р с надежностью 0,95, если в 80 испытаниях события А появилось 16 раз.

Решение: n = 80, m = 16, 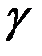= 0,95

– относительная частота появления А.

Найдем t из равенства Ф(t)= . Теперь по таблице функции Лапласа получим t = 1,96.

Подставив n = 80, = 0,2, t = 1,96 в формулы (3) и (4), получим, соответственно: 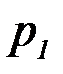= 0,128 = 0,299.

Ответ: 0,128 < р < 0,299.

Заметим, что при больших значениях n (порядка сотен) слагаемые и очень малы, и множитель . Тогда, в качестве приближенных границ доверительного интервала, можно принять:

,

.

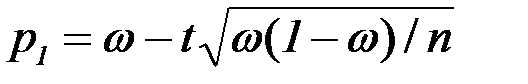Чтобы избежать расчетов концов доверительных интервалов можно использовать математико-статистические таблицы.

8.2.Доверительный интервал для оценки математического ожидания нормального распределения при известном среднем квадратическом отклонении.

Пусть генеральная совокупность распределена по нормальному закону, причём среднее квадратическое отклонение этого распределения известно.

Требуется оценить неизвестное математическое ожидание по 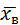. Найдём доверительный интервал, покрывающий параметр с надёжностью .

В качестве точечных оценок параметров нормального закона возьмём 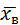и .

Вероятность заданного отклонения вычисляется по формуле:

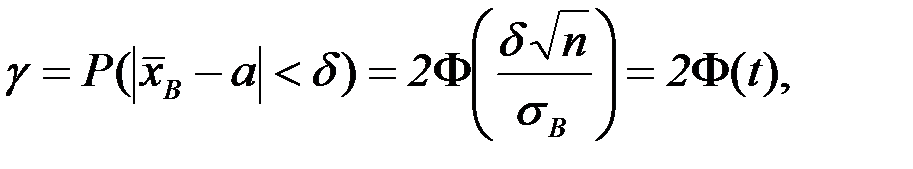
где

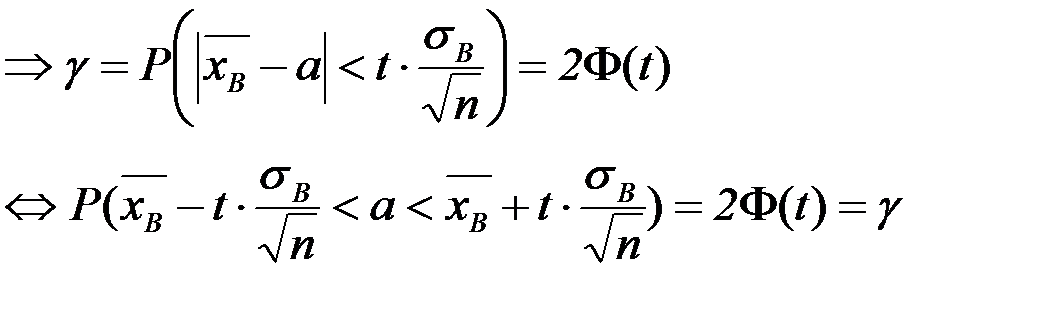
Для заданного по таблице функций Лапласа определяют квантиль для функции

Определение: Квантилью, или левосторонней критической областью, отвечающей вероятности , называется такая граница, левее которой вероятность равна .

Квантиль обозначается 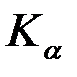. По определению 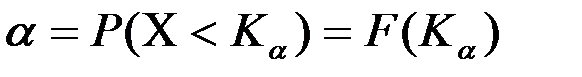, т.е. квантиль является решением уравнения .

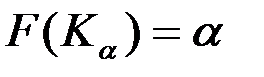Оценку называют классической. Из формулы можно сделать следующие выводы:

· при возрастании объёма выборки число убывает и, следовательно, точность оценки увеличивается;

· увеличение надёжности оценки приводит к увеличению 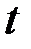( -возрастающая функция), следовательно, приводит и к возрастанию .

Другими словами, увеличение надёжности классической оценки влечёт за собой уменьшение её точности.

Пример: Случайная величина X имеет нормальное распределение с известным .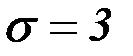

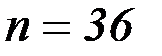Найти доверительные интервалы для оценки неизвестного математического ожидания по , если объём выборки и задана надёжность оценки .

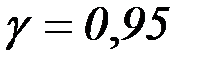Решение: 1)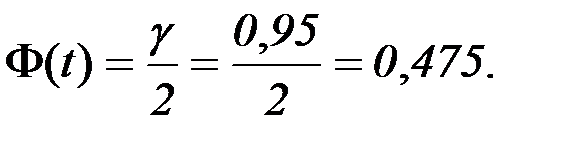

По таблице находим .

2) Найдём точность оценки:

3) Доверительный интервал: ()

Так как , то доверительный интервал имеет следующие доверительные границы:

Значения неизвестного параметра , согласующиеся с данными выборки, удовлетворяют неравенству: .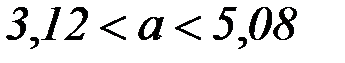

При этом надёжность указывает, что если произведено достаточно большое число выборок, то 95% из них определяет такие доверительные интервалы, в которых параметр действительно заключён; лишь в 5% случаев он может выйти за границы доверительного интервала.

Если требуется оценить математическое ожидание с заранее заданной точностью и надёжностью , то минимальный объём выборки, который обеспечит эту точность, находят по формуле:

(следствие равенства ).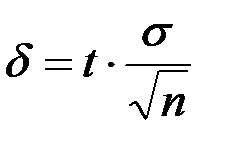

Дата добавления: 2014-12-27