Основные положения теоретической модели

Описание любой экспериментальной ситуации даётся теоретической моделью. Только в рамках принятой модели возможно косвенное определение тех или иных физических величин. В данной работе, в частности, косвенно определяется момент инерции различных тел (I).

Любая теоретическая модель даёт лишь приближенное описание экспериментальной ситуации, поскольку пренебрегает влиянием многих реально имеющих место эффектов. Сложность модели и определяется, главным образом, числом учитываемых эффектов.

Ниже кратко даётся информация по используемой в работе модели, необходимая для выполнения работы и обработки результатов измерений.

I. Диссипативными силами, т. е. силами трения, сопротивления воздуха и т. д., можно пренебречь в том смысле, что период крутильных колебаний системы в том случае, если бы они отсутствовали, пренебрежимо мало отличался бы от того, который наблюдается реально.

Ниже приводится оценка влияния диссипативных сил на период крутильных колебаний.

2. В работе изучаются крутильные колебания рамки с закреплёнными в ней различными телами: стержнем, цилиндром, параллелепипедом и т. д. Закрепление цилиндра, параллелепипеда, шара, конуса в рамке, а также их крепление к стержню осуществляется с помощью небольших штырьков. В теоретической модели, во-первых, предполагается, что оси, на которых лежат эти штырьки, проходят через центры масс соответствующих тел, во-вторых, что крепление обеспечивает параллельность этих осей и оси, вокруг которой совершаются колебания (оси, на которой расположены проволоки, крепящие рамку.)

3. Считается, что вся конструкция, участвующая в крутильных колебаниях, симметрична относительно оси колебаний. Например, при закреплении в рамке стержня с прикреплёнными к нему телами, тела должны быть одинаковыми и располагаться симметрично относительно центра стержня.

Задание 1. Определение момента инерции рамки (I_р) и коэффициента упругих сил кручения (C).

1. Определите период колебаний рамки без закреплённых в ней тел (Т₁) по методике, описанной выше.

Теория даёт следующее выражение для периода:

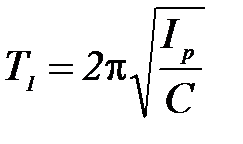, (1)

где I_р – момент инерции рамки без закреплённых в ней тел;

С – коэффициент упругих сил кручения;

2. Измерьте период колебаний рамки с кубом (Т₂).

Закрепите в рамке эталонный куб в центрах противоположных граней и найдите период Т₂₁ колебаний системы (рисунок 2). Повторите измерения для остальных двух пар противоположных граней, найдя Т₂₂; Т₂₃. Усредняя найденные значения, найдите период Т₂ колебаний рамки с закрепленным в ней эталонным кубом: Рисунок 2

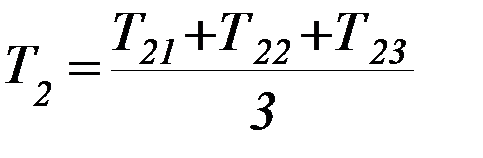
Теория даёт следующее выражение для периода колебаний рамки с закреплённым в ней кубом:

, (2)

где m – масса куба; а – сторона куба (указаны на рабочем месте), С – постоянная упругих сил кручения.

3. Из системы уравнений (1) и (2) найдите I_р и С.

4. Рассчитайте относительную погрешность определения момента инерции рамки (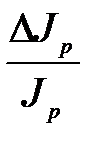) и коэффициента упругих сил кручения () как сумму относительных погрешностей прямым образом измеренных величин.

Относительные погрешности прямым образом определяемых величин (m, T, a) принять равными: ; ; .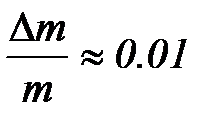

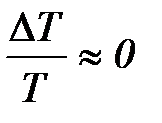Задание 2. Определение момента инерции груза (I_гр)

1. Измерьте период колебаний рамки со стержнем (Т₃). Для этого закрепите в рамке длинный стержень так, чтобы ось колебаний проходила через его центр (рисунок 3) и измерьте период Т₃ колебаний рамки со стержнем. Убедитесь, что период Т₃ практически не зависит от угла между плоскостью рамки и стержнем. Если эта зависимость присутствует, следует более аккуратно крепить стержень в рамке, соблюдая перпендикулярность стержня к оси колебаний и повторить

измерение Т_3. Рисунок 3

Вследствие аддитивности момента инерции согласно теории имеем:

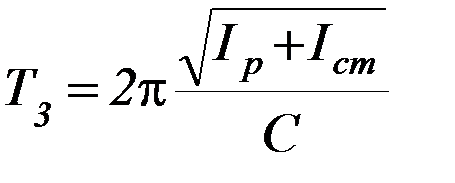, (3)

где I_ст – момент инерции стержня;

2. Из формулы (3), зная I_p из предыдущего задания, найдите момент инерции I_ст.

3. Прикрепите к стержню, закрепленному в рамке, симметрично два одинаковых тела с помощью штырьков, име­ющихся на этих телах, на расстоянии d от стержня (рис. 4). Рисунок 4

4. Найдите период колебаний конструкции из стержня и двух тел (Т₄) Рисунок 4

(4)

5. Из формулы (4) найдите момент инерции груза (I_гр) и сравните его с теоретическими значениями, найденными по формулам (5) и (6). По теореме Гюйгенса-Штейнера (см. Приложение):

, (5)

где R – радиус груза.

Если грузы одеть иначе (рисунок 5), то момент инерции груза относительно оси вращения будет равен

Рисунок 5

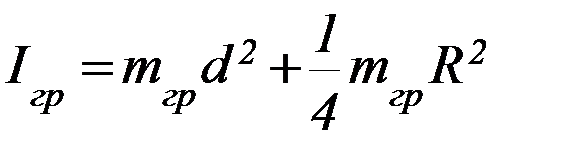(6)

Внимание: все измерения проводить по 3 раза и для расчётов брать среднее значение.

6. Рассчитайте относительную погрешность определения момента инерции груза (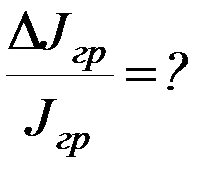) как сумму относительных погрешностей момента инерции рамки и коэффициента упругих сил кручения.

Относительной погрешностью определения периода в силу малости можно пренебречь . Относительные погрешности момента инерции рамки и коэффициента упругих сил кручения взять из предыдущего задания.

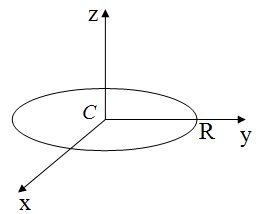
Приложение. Момент инерции и его вычисление.

Пусть твёрдое тело вращается вокруг оси Z (рисунок 6). Его можно представить как неизменную с течением времени систему разных материальных точек m_i, каждая из которых движется по окружности радиусом r_i, лежащей в плоскости, перпендикулярной оси Z. Угловые скорости всех материальных точек одинаковы. Моментом инерции тела относительно оси Z называется величина:

,

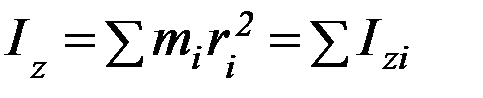где 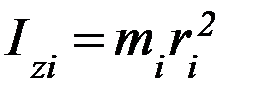– момент инерции отдельной материальной точки относительно оси ОZ. Из определения вытекает, что момент инерции – аддитивная величина, т. е. момент инерции тела, состоящего из отдельных частей, равен сумме моментов инерции частей.

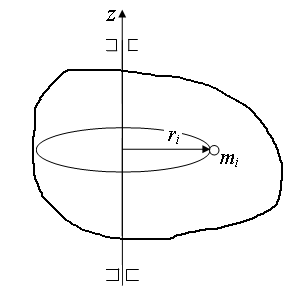
Рисунок 6

Очевидно, [ I ] = кг×м². Важность понятия момента инерции выражается в трёх формулах:

; ; .

Первая из них выражает момент импульса тела, которое вращается вокруг неподвижной оси Z (полезно эту формулу сравнить с выражением для импульса тела P = mV_c, где V_c – скорость центра масс). Вторая формула носит название основного уравнения динамики вращательного движения тела вокруг неподвижной оси, т.е., иначе говоря, второго закона Ньютона для вращательного движения (сравним с законом движения центра масс: 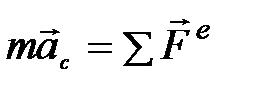). Третья формула выражает кинетическую энергию тела, вращающегося вокруг неподвижной оси (сравним с выражением для кинетической энергии частицы ). Сравнение формул позволяет сделать вывод о том, что момент инерции во вращательном движении играет роль, аналогичную массе в том смысле, что чем больше момент инерции тела, тем меньше угловое ускорение при прочих равных условиях оно приобретает (тело, образно говоря, труднее раскрутить). Реально вычисление моментов инерции сводится к вычислению тройного интеграла и может быть произведено лишь для ограниченного числа симметричных тел и лишь для осей симметрии. Количество осей, вокруг которых может вращаться тело, бесконечно велико. Среди всех осей выделяется та, которая проходит через замечательную точку тела – центр масс (точку, для описания движения которой достаточно представить, что вся масса системы сосредоточена в центре масс и к этой точке приложена сила, равная сумме всех сил). Но осей, проходящих через центр масс, также бесконечно много. Оказывается, что для любого твёрдого тела произвольной формы существуют три взаимно перпендикулярных оси С_х, С_у, С_z, называемые осями свободного вращения, обладающие замечательным свойством: если тело закрутить вокруг любой из этих осей и подбросить вверх, то при последующем движении тела ось останется параллельной самой себе, т.е. не будет кувыркаться. Закручивание вокруг любой другой оси этим свойством не обладает. Значение моментов инерции типичных тел относительно указанных осей приведено ниже. Если ось проходит через центр масс, но составляет углы a, b, g с осями С_х, С_у, С_z соответственно, то момент инерции относительно такой оси равен

I_c = I_cxcos²a + I_cycos²b + I_czcos²g (*)

Рассмотрим кратко вычисление момента инерции для простейших тел.

1. Момент инерции длинного тонкого однородного стержня относительно оси, проходящей через центр масс стержня и ему перпендикулярной.

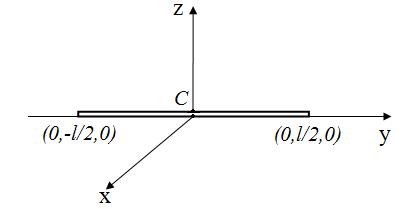Пусть т – масса стержня, l – его длина.

,

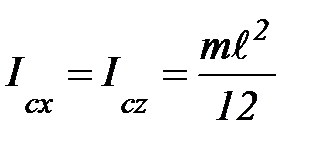Индекс «с» у момента инерции I _c означает, что это момент инерции относительно оси, проходящий через точку центра масс (центр симметрии тела), C(0,0,0).

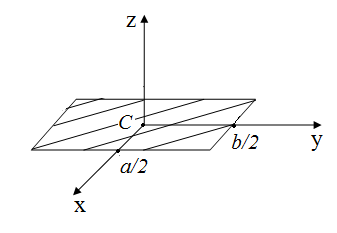
2. Момент инерции тонкой прямоугольной пластинки.

; ;

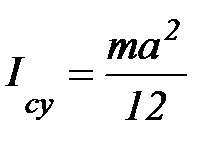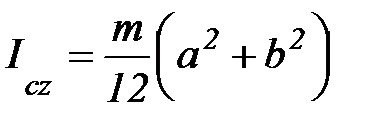
3. Момент инерции прямоугольного параллелепипеда.

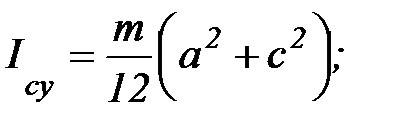
, т. С(0,0,0)

4. Момент инерции тонкого кольца.

;

, т. С(0,0,0)

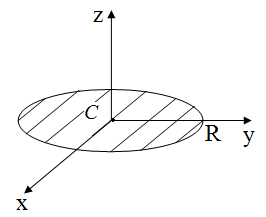5. Момент инерции тонкого диска.

В силу симметрии

; ;

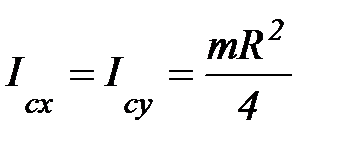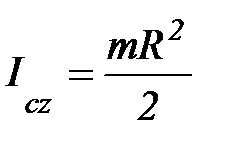
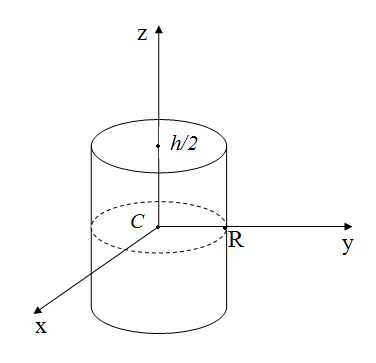6. Момент инерции сплошного цилиндра.

;

В силу симметрии:

7. Момент инерции сплошного шара.

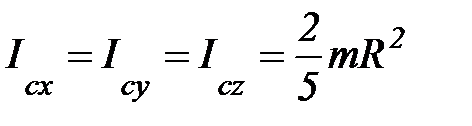, т. С(0,0,0)

8. Момент инерции сплошного конуса.

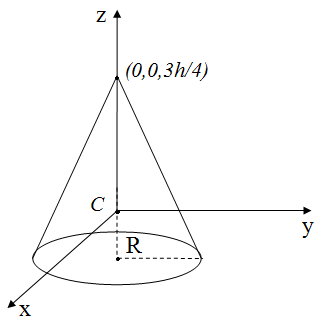
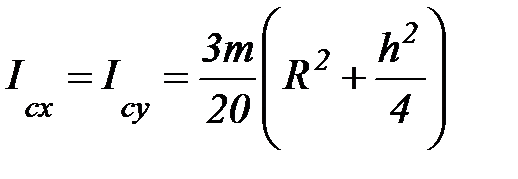
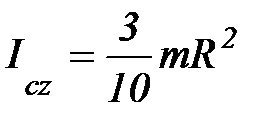, т. С(0,0,0)

где R – радиус основания, h – высота конуса.

Напомним, что cos²a + cos²b + cos²g = 1. Наконец, если ось О не проходит через центр масс, то момент инерции тела может быть вычислен с помощью теоремы Гюйгенса Штейнера

I_о = I_с + md², (**)

где I_о – момент инерции тела относительно произвольной оси, I_с– момент инерции относительно параллельной ей оси, проходящей через центр масс,
m– масса тела, d– расстояние между осями.

Процедура вычисления моментов инерции для тел стандартной формы относительно произвольной оси сводится к следующему:

1. Проведите ось, параллельную данной оси О и проходящую через центр масс.

2. Находите углы a, b, g между осями С_х, С_у, С_z, совпадающими с осями вращения и показанными на рисунках, и осью С и по формуле (*) находите I_c.

3. По формуле (**) находите искомый момент инерции.

В качестве примера определим момент инерции цилиндра в ситуации, показанной на рисунке (см. ниже).

Здесь ось О лежит в плоскости YСZ, ось OX перпендикулярна этой плоскости, поэтому

; ; ;

,

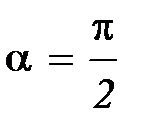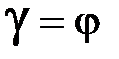тогда:

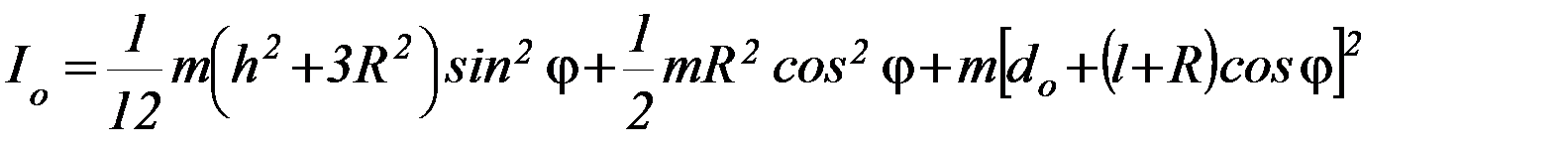
Заметим, наконец, что в реальной практике приходится определять момент инерции тел достаточно сложной формы. Это связано в частности с тем, например, что напряжения, возникающие в упругом теле при изгибе и кручении, зависят от моментов инерции, а значения этих напряжений необходимы во многих задачах. Вычисление моментов инерции в таких случаях достаточно затруднительно, поэтому разумно использовать экспериментальные методы. Один из таких методов и рассмотрен в данной работе.

Контрольные вопросы.

1. Сформулируйте основное уравнение динамики твёрдого тела для вращательного движения относительно неподвижной оси.

2. Запишите момент инерции материальной точки, системы материальных точек и однородного тела.

3. Приведите аналогии между кинематическими характеристиками вращательного и поступательного движений абсолютно твёрдого тела; то же для динамических характеристик.

4. В чём причины возникновения ошибок в ходе эксперимента?

5. Прямые измерения каких физических величин позволяет проводить данная установка?

6. Какие физические величины возможно косвенно определить в данной работе в рамках предложенной модели?

7. Назовите основные положения предложенной теоретической модели для данной установки.

8. Какие оси называются «Осями свободного вращения»?

9. Как записать момент инерции твёрдого тела относительно центра масс тела, выраженный через проекции на оси свободного вращения?

10. Получите выражение для момента инерции стержня относительно оси, проходящей через центр масс стержня и перпендикулярной ему.

11. Получите выражение для момента инерции стержня относительно оси, проходящей через конец стержня и перпендикулярной ему.

12. Получите выражение для момента инерции диска относительно оси, проходящей через его центр масс и перпендикулярной плоскости диска.

Дата добавления: 2014-12-27