Альтернативный оптимум

При решении задач линейного программирования сим­плексным методом критерием оптимальности является условие 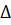_J 0 для задач на максимум и условие 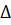_J < 0 для задач на минимум. Если на каком-то шаге окажется, что хотя бы одна оценка свободной переменной 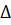_J = 0, а все остальные 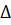_J > О для задач на максимум ( 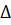_J < 0 для задач на минимум), то, приняв в качестве ключевого столбца столбец, где 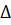_J = 0, и найдя новое оптимальное решение, заметим, что значение це­левой функции при этом не изменится. Говорят, что в этом случае задача имеет альтернативный оптимум.

Критерием альтернативного оптимума при решении за­дач симплексным методом является равенство нулю хотя бы одной оценки свободной переменной (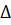 _J = 0).

Если только одна оценка свободной переменной равна ну­лю, то решение находится по формуле

опт =t опт ₁+(1-t) 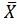опт _2,

где 0 t 1.

Если две оценки и более, например 5, свободных перемен­ных равны нулю, то оптимальное решение определяется по формуле

опт = ,

где ,t_i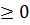

В задачах, имеющих альтернативный оптимум, возникает возможность включения в ее модель других критериев эффек­тивности.

Пример. Дана задача линейного программирования

L() = 2X₁ — 4X₃+ 2X₅ min

при ограничениях:

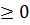x_{j ,} j=

РЕШЕНИЕ. Составим симплексную таблицу (табл. 4.7).

В индексной строке имеется одна положительная оцен­ка. Полученное решение можно улучшить. Ключевым элемен­том является 4.Составляем симплексную таблицу 2-го шага (табл. 4.8). Получаем опт ₁ = (10, 0, 3,0,0).

Таблица 4.7

Ci	БП			-4			L(x)
Xl	Х2	Xз	Х4	Х5	bi
	X1			-1
	X4		-2
Δj		-2
Таблица 4.8
	БП			-4			L(x)
Ci	Xl	Х2	Xз	Х4	Х5	bi
	X1		5/2 -1/2		1/4 1/4
-4	Хз		1/2
Δj				-1	-2	-12
Таблица 4.9
Ci	БП			-4			L(x)
Xl	Х2	X3	Х4	X5	bi
	Х2	2/5			1/10	4/5
-4	X3	1/5			3/10	9/10
Δj				-1	-4	-12

Так как Δ2= 0, то задача имеет альтернативный оптимум. Найдем еще одно оптимальное решение, введя вместо базисной переменной X1 свободную переменную X2 (табл. 4.9). Получаем Xопт2 = (0,4,5,0,0).

Найдем координаты оптимального решения задачи:

X1 = 10t + (1-t)0 = 10t,

X2 = 0t + (1 - t)4 = 4 - 44,

X3 = 3t + (1 -t)5 = -2t + 5,

X4 = 0t + (1 - t)0 = 0,

X5 = 0t + (1 - t)0 = 0,

Xопт = (10t,4 - 4t, 5 - 2t,0,0).

Давая t значения из [0,1], получим различные Хопт, при кото­рых L(х) = -12.

УПРАЖНЕНИЯ

Решить следующие задачи симплексным методом.

4.1 L(x) - X1 – 3X2 — 5X3 — X4 —> max при ограничениях:

X1 + 4X2 + 4X3 +X4 = 5,

X1 + 7X2 + 8X3 + 2X4 = 9,

Xj > 0 j = 1.4

4.2 L(x) = X1 + 2X2 + ЗX3 —> min при ограничениях:

X1 + 2X2 + ЗX3 + Х4 = 10,

2X1 + X3 = 3,

X1 + X2 + 2X3 = 6,

Xj > 0, j = 1.4.

4.3 L(x) = -2X1 - Х2 + X3 + Х4 —> шах при ограничениях:

X1 - X2 + 2X3 - X4 = 2,

2X1 + Х2 – ЗX3 + Х4 = 6,

X1 + Х2 + Х3 + Х4 = 7,

Xj > 0, j = 1.4.

4.4 L(x) = 3X1 + Х2 + 2X3 —> min при ограничениях:

2X1 + X2 + X3 = 40,

X1 +2X2 + 2X3 = 10,

Xj > 0, j=1.3.

4.5 L(x) = xi + X2 + X3à max при ограничениях:

3X1 + X2 — X3 = 5,

3X1 + 2X2 + X3 = 7,

Xj >0, j = 1,3.

4.6 L(x) = X1 + 2X2 + 2i3 à min при ограничениях:

X1 + X2 + X3 > 4,

X1 — X2 + X3 > 2,

Xj >0, j = 1,3.

4.7 L(x) = 3X1 + X2 + X3 + X4 max при ограничениях:

2X1 + X2 + 4X3 + ЗХ4 < 3,

3X1 — X2 + 2X3 + 5X4 < 1,

Xj > 0, j = 1.4.

4.8 L(x) = X1 — 5X2 — X3 max при ограничениях:

X1 + 3X2 + ЗХ3 = 3,

2X1 + ЗX3 < 4,

Xj >0, j = 1.3

4.9 L(x) = X1 + X2 + X3 + X4 à min при ограничениях:

3X1 + 2X2 + X3>8,

X1 + 6X2 + 9X3 + 1ЗХ4 > 4,

Xj >0, j = 1.4

4.10 L(x) = 3X1 + 5X2 + 4X3 à max при ограничениях:

ЗX1 + 4X2 + 2X3 < 9,

2X1 + 5X2 + X3 < 8,

X1 + 2X2 + 4X3 > 7,

Xj ^ 0, j = 1.З.

4.11 Механический завод при изготовлении двух типов дета­лей использует токарное, фрезерное и сварочное оборудование. При этом обработку каждой детали можно вести двумя раз­личными технологическими способами. Необходимые исход­ные данные приведены в табл. 4.10.

Составить оптимальный план загрузки оборудования, обес­печивающий заводу максимальную прибыль.

Таблица 4.10

	Детали
Оборудование			Полезный фонд времени,
Технологические способы
					станко-ч
Фрезерное
Токарное
Сварочное
Прибыль, усл. ед.

4.12. Торговая фирма для продажи товаров трех видов ис­пользует ресурсы:1 время и площадь торговых залов. Затраты ресурсов на продажу одной партии товаров каждого вида да­ны в табл. 4.11. Прибыль, получаемая от реализации одной партии товаров 1-го вида, — 5 усл. ед., 2-го вида — 8 усл. ед., 3-го вида — 6 усл. ед.

Определить оптимальную структуру товарооборота, обес­печивающую фирме максимальную прибыль

Таблица 4.11

Ресурсы	Вид товара	Объем
			ресурсов
Время,чел.-ч	0,5	0,7	0,6
Площадь, м2	0,1	0,3	0,2

4.13. Фирма выпускает четыре пользующихся спросом изде­лия, причем месячная программа выпуска составляет 10 изде­лий типа 1 и 3, 200 изделий типа 2 и 120 изделий типа 4. Нормы затрат сырья на единицу различных типов изделий приведены в табл. 4.12.

Таблица 4.12

Вид	Нормы затрат на одно изделие	Запасы
сырья					сырья, ед.
					600.

Прибыль от реализации изделий типа 1 равна 6 усл. ед., изделий типа 2 — 2 усл. ед., изделий типа 3 — 2,5 усл. ед. и изделий типа 4 — 4 усл. ед.

Определить, является ли месячная программа выпуска из­делий оптимальной, и если нет, то определить оптимальную месячную программу и дополнительный доход, который фир­ма может при этом получить.

4.14. Металлургический завод из металлов A1, А2, А3 может выпускать сплавы В1, В2, В3. В течение планируемого пери­ода завод должен освоить не менее 640 т металла A1 и 800 т металла А2, при этом металла A3 может быть израсходовано не более 860 т. Определить минимальные затраты, если данные о нормах расхода и себестоимость даны в табл.4.13

Таблица 4.13

Вид	Технологические нормы расхода металла на усл. ед. сплава	Наличие металла у завода
Металлов	В1	в2	В3
A1	1,0	4,3	2,6
А2	5,0	1,5	3,0
А3	3,0	3,9	4,3
Себестоимость 1т сплава

4.15. Ткань трех артикулов производится на ткацких станках двух типов с различной производительностью. Для изготов­ления ткани используются пряжа и красители. В табл. 4.14 указаны мощности станков в тысячах станко-часов, ресурсы пряжи и красителей в 1000, производительности станков в метрах за час, нормы расхода пряжи и краски в килограммах на 1000 м и цена 1 м ткани.

Таблица 4.14

Вид	Объем	Нормы расхода
ресурсов	ресурсов
Станки 1-го типа
Станки 2-го типа
Пряжа
Красители
Цена, усл. ед.

По этим исходным данным решить следующие задачи:

1) определить оптимальный ассортимент, максимизирую­щий товарную продукцию предприятия;

2) приняв условие, что количество тканей трех артикулов находится в отношении 2:1:3, определить, какое мак­симальное количество комплектов ткани может выпус­тить предприятие;

3) определить оптимальный ассортимент, максимизирую­щий доход предприятия, если цена 1 м ткани составляет 8, 5 и 15 усл. ед. соответственно;

4) решить задачу (1) при, условии, что станки 1-го типа ткань первого артикула не производят.

Тема 5.ТРАНСПОРТНАЯ ЗАДАЧА

Математическая постановка задачи состоит в определении оптимального плана перевозок некоторого груза из m пунктов отправления A₁, A₂, …, A_m в n пунктов назначения B₁, B₂, …, B_n. При этом в качестве критерия оптимальности обычно выбирается либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки.

Обозначим через C_ij стоимость перевозки единицы груза из i –го пункта отправления в j –й пункт назначения; а_i - запасы груза в i –м пункте отправления (величина предложения); b_j - потребности в этом грузе в j –м пункте назначения (величина спроса); X_ij - объем перевозок (количество перемещаемых единиц груза) из i –го пункта отправления в j –й пункт назначения. Тогда математическая модель транспортной задачи имеет следующий вид: определить минимум целевой функции

f(x) = ® min (5.1)

при выполнении следующих ограничений:

= а_i; i = 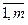, (5.2)

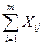= b_j; j = 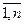, (5.3)

Х_ij ³ 0; i = 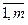; j = 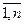. (5.4)

Обычно исходные данные транспортной задачи представляются в виде таблицы. Внутренняя часть этой таблицы является объединением двух матриц: матрицы перевозок Х = { X_ij } и матрицы стоимостей С = { С_ij }.

Пункты отправления	Пункты назначения	Запасы (предложение)
В1	В2	…	Вj	…	Вn
А1	С11 Х11	С12 Х12	…	C1j Х1j	…	C1n Х1n	а1
А2	С21 Х21	С22 Х22	…	C2j Х2j	…	C2n Х2n	а2
…	…	…	…	…	…	…	…
Аi	Сi1 Хi1	Сi2 Хi2	…	Сij Хij	…	Сin Хin	аi
…	…	…	…	…	…	…	…
Аm	Сm1 Хm1	Сm2 Хm2	…	Сmj Хmj	…	Сmn Хmn	аm
Потреб-ности (спрос)	b1	b2	…	bj	…	bm	Sbj = Sаi

Если общий запас груза у поставщиков равен потребности в грузе у потребителей, т.е. если выполняется условие

= , (5.5)

то модель такой транспортной задачи называется закрытой, а если условие не выполняется, то задача называется открытой.

Определение 1. Всякое неотрицательное решение систем линейных уравнений (2) и (3), определяемое матрицей Х = { X_ij }; i = 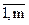; j = 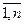, называется планом транспортной задачи.

Определение 2. План Х* = {X_ij*}, при котором функция цели 1 принимает минимальное значение, называется оптимальным планом транспортной задачи.

Ограничения 2 и 3 транспортной задачи представляют собой две группы уравнений. Первая из них, т.е. система уравнений 2, означает то, что сумма перевозок по каждой строке таблицы должна быть равна соответствующему запасу а_i. Каждое уравнение второй системы 3 означает то, что сумма перевозок по каждому столбцу таблицы должна быть равна соответствующей потребности b_j. Транспортная задача представляет собой задачу линейного программирования, записанную в каноническом виде. Следовательно, ее можно решать симплексным методом. Однако для решения транспортных задач существуют специальные методы.

Особенности транспортной задачи:

1. Закрытая транспортная задача всегда совместна, обладает планом, т.е. имеет решение.

2. Если значения и а_i-е и b_j-е – целые и неотрицательные, то транспортная задача имеет целочисленное решение.

3. Клетки таблицы транспортной задачи с координатами, в которых проставлены значения перевозок, называются базисными и соответствуют базисным переменным, а остальные клетки остаются свободными. Для невырожденного опорного плана в таблице транспортной задачи будет заполнена положительными числами m + n – 1 клетка. Если же опорный план задачи вырожден, то часть базисных клеток будет заполнена нулями.

Дата добавления: 2014-12-27