В психологии

ПРОСТЕЙШИЕ МЕТОДЫ АНАЛИЗА ДАННЫХ

Калинин А.А., Гусева С.И.

Учебно-методическое пособие

Санкт-Петербург

Рецензенты:

Благинин А.А., доктор медицинских наук, профессор (Военно-медицинская академия, Санкт-Петербург)

Маклаков А.Г., доктор психологических наук, профессор, (Ленинградский государственный университет им. А.С. Пушкина)

Калинин А.А., Гусева С.И. Простейшие методы анализа данных в психологии. Учеб.-метод. пособие. СПб: ЛГУ им. А.С. Пушкина, 2004

Пособие представляет собой практическое руководство для студентов при статистическом обосновании научных и практических выводов курсовых и дипломных работ. Принцип отбора методов – ясность и простота. Методы рассматриваются на реальных примерах и сопровождаются алгоритмами.

Все они могут быть использованы для быстрой обработки данных.

Руководство предназначено для студентов и практических психологов образовательных учреждений.

ISSN 5-8290-0456-5

ВВЕДЕНИЕ.. 5

1. ШКАЛЫ... 6

2. СЛУЧАЙНОЕ СОБЫТИЕ.. 8

3. СЛУЧАЙНАЯ ВЕЛИЧИНА.. 10

3.1 Распределение случайной величины.. 10

3.2 Параметры распределения. 12

3.3 Нормальное распределение. 17

4. ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ И ВЫБОРКА.. 20

5. СТАНДАРТИЗАЦИЯ ПСИХОДИАГНОСТИЧЕСКИХ МЕТОДОВ.. 21

6. СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ... 24

7. МАТЕМАТИЧЕСКИЙ АППАРАТ ПРОВЕРКИ СТАТИСТИЧЕСКИХ ГИПОТЕЗ. 27

7.1. Подготовка данных. 28

7.1.1 Порядок выявления аномальных значений. 28

7.1.2 Проверка эмпирического распределения на его соответствие нормальному распределению.. 30

7.2 Сравнение среднего значения некоторой выборки со средним значением генеральной совокупности или с нормативным значением.. 36

7.3 Сравнение уровня признака. 37

7.4 Сравнение уровня признака в зависимых выборках. 43

7.5 Оценка сходства-различия распределений признаков. 48

8. ИЗУЧЕНИЕ ВЗАИМОСВЯЗИ ПСИХОЛОГИЧЕСКИХ ЯВЛЕНИЙ.. 51

8.1 Меры связи явлений, измеренных в номинативных шкалах. 51

8.2 Корреляционная связь. 55

8.2.1 Меры связи для явлений, измеренных в ранговых шкалах. 58

8.2.3 Меры связи для явлений, измеренных. 63

8.3 Корреляционный анализ. 65

Список использованной литературы: 69

Дополнительная литература: 69

Приложение 1. Таблицы критических значений. 70

Значения кумулятивной функции распределения. 70

стандартного нормального распределения. 70

Таблица критических значений параметра «а» для исключения выскакивающих значений. 71

Таблица критических значений критерия c² Пирсона. 71

Критические значения F-критерия Фишера. 72

Таблица критических значений t-критерия Стьюдента. 73

Таблица критических значений критерия Манна-Уитни. 74

Таблица критических значений Т-критерия Вилкоксона для множественных сравнений. 75

Таблица критических значений Т-критерия Вилкоксона для попарных сравнений. 76

Таблица критических значений L-критерия Пейджа. 77

Таблица критических значений коэффициента корреляции Спирмена. 78

Таблица критических значений коэффициента корреляции Пирсона. 78

Приложение 2. 79

. Результаты ШТУР, использованные при составлении задач настоящего методического пособия. 79

ВВЕДЕНИЕ

Одной из наиболее важных особенностей развития познания в ХХ веке является математизация всех наук, включая естественные и гуманитарные. Не стала исключением и психология: переход от описания явления к его измерению и активное экспериментирование способствовали внедрению математических методов обработки данных в практику психологов даже несколько ранее, чем это произошло в других гуманитарных науках. Более того, целый ряд широко используемых в гуманитарных и естественных науках статистических методов нашел свое распространение именно благодаря исследованиям психологов.

Современная культура экспериментального исследования в любой области знаний требует убедительных статистических подтверждений. Математические методы применяются в психологии в первую очередь для правильного описания, обобщения и представления получаемых результатов. Математическая обработка данных позволяет выявить и в обобщенном виде описать закономерности психологических явлений, нередко способствует пониманию их сути и, самое главное, повышает доказательность выводов. Математический аппарат статистических исследований универсален: психологи используют математические методы, разработанные для решения задач экономики, биологии, геологии, в то же время методы, разработанные для решения собственно психологических задач, успешно применяются специалистами в области естественных наук.

Любому психологу-практику следует иметь представление о той математике, которая лежит в основе психологической диагностики, чтобы математически правильно понимать и интерпретировать результаты тестирования. Первичные результаты любого психологического теста практически бессмысленны без дополнительных данных. Сказать, что кто-то правильно решил 10 задач теста, опознал 24 слова в лексическом тесте или собрал тестовый объект из элементов за 52 секунды - это практически ничего не сообщить о том, как у этого объекта исследований развита соответствующая функция. Точно так же, если мы приведем не абсолютные, а процентные показатели, например, выполнения заданий - 65% правильных ответов по одному тесту, 28% по другому, 80% по третьему, то мы опять же не дадим практически никакой новой информации, поскольку мы не знаем сложности выполненного задания. Любые первичные данные могут быть истолкованы только в рамках какой-либо четко заданной единой системы отсчета. В психологии результаты тестов чаще всего интерпретируется путем их сравнения с нормами выполнения, установленными опытным путем. Решить, как соотносятся результаты исследования с нормативными показателями (различаются значимо, незначимо, либо не отличаются) - это задача, решаемая с применением методов математической статистики. Методы математической статистики позволяют сравнить показатели двух обследуемых групп между собой, установить, значимо ли изменились показатели одного обследуемого или целой группы после воздействия какого-либо внешнего фактора, установить наличие или отсутствие согласованности изменения двух и более величин. Математическая статистика позволяет оценить, насколько можно доверять тому или иному выводу исследователя, но при этом ни в коем случае не служит его доказательством.

Математический аппарат статистических исследований, описанных в настоящем пособии, как правило, совсем несложен и ограничивается четырьмя арифметическими действиями и возведением в степень, что делает материал доступным даже для студентов, считающих себя абсолютно неспособными к математике. В рамках курса использованы наиболее простые примеры, что облегчает понимание сути метода. Все расчеты при решении задач могут быть выполнены с помощью калькулятора. Как правило, в распоряжении современного исследователя есть компьютер, для которого написано множество программ расчета статистических характеристик. В практической работе в дальнейшем, в том числе при выполнении курсовых и дипломных работ, для работы с большими выборками данных можно и нужно использовать возможности их компьютерной обработки. В пособии указаны статистические критерии, расчет которых можно провести с помощью программы Microsoft Excel.

1. ШКАЛЫ

Перед тем, как приступить к обработке данных, надо привести эти данные в соответствующий вид. Математическая обработка данных - это оперирование со значениями какого-либо признака, полученными в результате психологического исследования. Это могут быть, к примеру, время решения задачи, или количество допущенных ошибок при чтении текста, или количество родителей, поддержавших введение новой школьной программы и множество других переменных. То есть математическая обработка данных - это исследование результатов измерения признаков. Под измерением признака понимается приписывание объектам или событиям числовых форм в соответствии с определенными правилами. С.Стивенс выделил 4 способа измерения признаков, которые он назвал шкалами: это шкалы наименований (синонимы - «номинативная» и «номинальная»), рангов (она же порядковая шкала), интервалов и отношений. Первые две шкалы - наименований и рангов - относятся к неметрическим шкалам, поскольку непосредственно чисел они явлениям не приписывают. Две другие шкалы - интервалов и отношений - относятся к шкалам метрическим.

Шкала наименований, она же номинативная или номинальная шкала. Понятно, что наименование не измеряется количественно, оно лишь позволяет отличить один предмет (явление) от другого. Номинативная шкала - это способ распределения объектов или явлений по классификационным ячейкам. Например, проголосовал «за» - проголосовал «против», или «русский» - «иностранец», или ответил на вопрос «да» или «нет». В простейшем случае номинативная шкала состоит из двух ячеек («да - нет»), и она называется дихотомической. Более сложный вариант номинативной шкалы - классификация из трех и более ячеек («за» - «против» - «воздержался», ездит на работу автобусом - трамваем - троллейбусом - метро и т.д.). Исследователь постоянно сталкивается с номинативной шкалой при обработке результатов социологических и социально-психологических опросов и анкет. Испытуемый, выбирая один из возможных ответов, относит себя к тому или иному классу (категории) людей, причем категории являются взаимоисключающими. Категории можно называть буквами - А, Б, В, или, к примеру, по цвету - красный, синий, зеленый, или цифрами - номерами вопросов. Но номер вопроса в анкете - это только имя класса ответов, он не имеет метрического значения (мы не можем говорить, что «5 больше 3», а «2 в два раза больше 1»). Только распределив объекты или реакции испытуемых по ячейкам классификации и сосчитав количество наблюдений в каждой из ячеек, то есть частоту встречаемости того или иного признака, мы получаем возможность перейти от наименований к числам. Таким образом, при использовании шкалы наименований единицей измерения является «одно наблюдение».

Другая шкала - это шкала рангов (или порядковая шкала), которая классифицирует объекты по принципу «больше»- «меньше». Здесь мы группируем объекты в три или более классов, придавая, обычно, объектам с наименее выраженными свойствами наименьшее значение ранга (класса) - 1, с несколько более выраженными свойствами - 2, и так далее по возрастающей. Например, шкала рангов «подходит на должность директора фирмы» - «подходит при определенных условиях» - «не подходит» имеет три ранга - 3, 2 и 1 соответственно. Мы не знаем истинных отношений между классами, может быть классы 3 и 2 очень близки к друг другу, а класс 1 контрастно отличается, но знаем их последовательность от меньшего к большему. И, переходя от классов к обозначающим их числам, мы получаем возможность математической обработки данных. Естественно, чем больше выделено классов, тем шире эти возможности.

Все психологические методы, основанные на ранжировании, используют шкалу порядка. Например, распределяя 10 ценностей по их значимости лично для него, испытуемый совершает так называемое принудительное ранжирование, и количество рангов соответствует количеству ранжируемых объектов (субъектов). Разные ранги, таким образом, будут получать довольно близкие по своей ценности объекты. Например, в тесте при приеме на работу задается вопрос, что для Вас важнее - высокая зарплата, дружный коллектив, близость места работы к дому, свободный график работы и так далее. И хотя поступающему на работу может быть одинаково важно наличие дружного коллектива и близость к дому, но он вынужден задать эти двум категориям разные ранги. Бывает наоборот, что большое количество испытуемых или понятий надо «втиснуть» в 3-4 класса, при этом, разумеется, одинаковые ранги получит целая группа испытуемых, возможно, значительно различающихся между собой.

В порядковой шкале (шкале рангов) единица измерения - 1 класс (ранг). Расстояние между классами нам неизвестно, оно может быть одинаковым, может быть различным.

Шкала интервалов классифицирует объекты или явления по признакам «больше (меньше) на какое-то количество единиц», то есть основывается на предположении о равенстве разности степени выраженности какого-либо психологического свойства двух объектов разности двух чисел, приписываемых этим объектам для характеристики свойства.

Шкала отношений классифицирует объекты или субъекты пропорционально степени выраженности измеряемого свойства, то есть предполагает равенство отношения степени выраженности какого-либо психологического свойства двух объектов отношению двух чисел, приписываемых этим объектам для характеристики свойства. Принципиальная разница между шкалами интервалов и отношений заключается в том, что в интервальной шкале нет абсолютного нуля (нулевая точка ставится условно), в шкале отношений такая точка есть. По шкале отношений мы можем представить, во сколько раз свойство одного испытуемого превосходит свойство другого. Лучше всего представить себе разницу между шкалами интервалов и отношений на примере температурной шкалы. Шкала Цельсия - интервальная, разница температуры между -10°С и -20°С такая же, как между 150°С и 140°С. Но на шкале интервалов нет естественного нуля - значение 0°С по Цельсию выбрано произвольно, как точка замерзания воды. В абсолютной шкале Кельвина точка 0°К обозначает температуру, ниже которой значений быть не может. Следовательно, здесь есть абсолютный ноль, и шкала Кельвина является шкалой отношений. К этому же типу относятся измерения длины объектов. Может быть длина нулевая (нет объекта), но не может быть отрицательных значений. Шкала отношений - высшая форма измерений, с данными, измеренными в шкале отношений можно осуществлять все виды математических операций. Шкала отношений используется, в основном, при психофизиологических исследованиях явлений, измеряемых в физических единицах (метры, граммы, секунды и т.д.). Для большинства психологических явлений шкала отношений не применяется: трудно представить себе полное отсутствие у испытуемого какого-либо психологического свойства - например, абсолютную глупость. Итоговая оценочная шкала большинства опросников - интервальная, где точкой отсчета - условным нулем - является ноль набранных баллов.

При математической обработке данных в случае необходимости всегда можно перейти к шкале более низкого порядка - от шкалы интервалов, например, к шкале рангов или наименований. В то же время переход к шкале более высокого порядка (от шкалы наименований, к примеру, к шкале рангов) невозможен без дополнительных исследований.

2. СЛУЧАЙНОЕ СОБЫТИЕ

Случайным событием называется событие, которое может произойти либо не произойти, либо произойти в той или иной степени. Численными мерами появления случайного события являются абсолютная частота, относительная частота и вероятность.

Абсолютная частота - это просто количество событий, интересующих исследователя. Абсолютную частоту принято обозначать символом f_i.

Относительная частота - это абсолютная частота, отнесенная к общему количеству событий в некотором опыте.

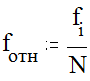
Вероятность - это то значение, к которому стремится относительная частота при бесконечном увеличении числа опытов. Выражается она в виде положительного числа, большего нуля и меньшего 1 (либо от 0 до 100%), и является понятием идеальным, поскольку на практике количество опытов всегда ограничено. Вероятность равна 0, если событие абсолютно невероятно, и равна 1 (или 100%) если событие неизбежно. Определяя вероятность какого-либо события как 1/2 или 50% («вероятность дождя завтра 50%») мы выражаем свою точку зрения с наименьшей степенью уверенности. Если же мы скажем, что вероятность дождя 75% (а того, что дождя не будет, соответственно, 25%) мы проявляем большую степень уверенности - вероятность дождя в три раза выше вероятности того, что дождя не будет. Вероятность принято обозначать буквой «р».

События А, В, С,... могут быть совместными и несовместными, зависимыми и независимыми. Совместными называются события, которые могут произойти одновременно в одном и том же опыте (длинный и зеленый, или, например, экстраверт-невротик). Несовместными будут события, которые одновременно произойти не могут (в одном опыте испытуемый не может быть сразу экстра- и интровертом, монета может упасть или «орлом», или «решкой»). Полной группой событий называется множество несовместных событий, одно из которых произойдет обязательно: испытуемый будет лицом женского или мужского пола, он будет старше 40 лет или не старше этого возраста.

Зависимыми называются события, появление одного из которых оказывает влияние на вероятность другого. Ребенок достиг семи лет, и он идет в школу. Ученик окончил первый класс, и он умеет писать буквы. Если такое влияние отсутствует, то события являются независимыми.

Суммой событий называется событие S, заключающееся в том, что произойдет или одно, или другое, или третье и т.д. событие, т.е. S=А+В+С+.... Произведением событий называется событие W, заключающееся в том, что произойдет и первое, и второе, и третье и т.д. событие: W=A^xB^xC^x.... Для сумм и произведений событий выполняются следующие правила:

1. Вероятность суммы несовместных событий равна сумме вероятностей этих событий Р(A+B+C+...) = P(A)+P(B)+P(С)+...P(Z). Например, нам известно, что среди студентов ВУЗа 40% сангвиников, 20% холериков, 24% флегматиков и 16% меланхоликов. Вероятность того, что первый встреченный нами студент окажется флегматиком составляет 24%, холериком или сангвиником 20+40=60%, меланхоликом или флегматиком 24+16=40%, а того, что он не окажется меланхоликом 84% (20+40+24%).

2. Вероятность произведения независимых событий равна произведению вероятностей этих событий Р(A×B×C×... ×Z) = P(A)×P(B)×P(С)... ×P(Z). К примеру, отвечая на вопросы экзаменационного тестирования, абитуриент уверен в правильности ответа на первый вопрос на 90%, на второй - на 100%, на третий - на 50%, на четвертый - на 60%. В этом случае вероятность полностью правильного выполнения теста Р= 0,9×1,0 × 0,5 × 0,6 = 0,27 или 27%.

3. СЛУЧАЙНАЯ ВЕЛИЧИНА

3.1 Распределение случайной величины

Случайной величиной называется такая переменная величина, которая принимает значения из некоторого множества. Принято выделять дискретные и непрерывные случайные величины. Дискретная случайная величина принимает свои значения из множества целых чисел - например, количество учеников в классе, количество несчастных случаев на производстве и так далее. Непрерывная случайная величина принимает свои значения из множества действительных чисел. Ряд психологических явлений непрерывен по своей природе. Это относится, например, к интеллекту, эмоциональности, тревожности, воображению и т.д. Чтобы описать и измерить такие явления, мы разбиваем числовую ось на равные интервалы. Например, возраст мы измеряем, как правило, интервалами, равными одному году. Время принято измерять интервалами, равными секунде, минуте, часу, суткам и т.д. Операция разбиения числовой оси на равные интервалы называется квантованием, а полученные интервалы - интервалами квантования.

Основной способ описания случайной величины - построение ее распределения. Для дискретной величины подсчитывают количество случаев, приходящихся на каждое значение (абсолютная частота), и затем строят гистограмму (столбчатую диаграмму), наглядно представляющую особенности распределения. На гистограмме по оси «Х» откладывается значение случайной величины, а по оси «Y» - абсолютная частота (Рис.1).

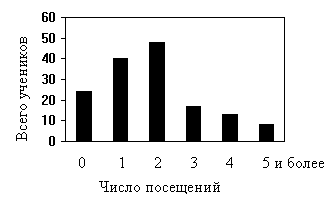
Рис 1. Гистограмма распределения количества посещений медицинского кабинета учениками школы в течение учебного года.

Для описания непрерывной случайной величины либо большого количества измерений дискретной случайной величины данные предварительно следует сгруппировать по интервалам квантования. Прежде всего, надо составить таблицу частотного распределения. Данные группируются по интервалам квантования, и подсчитывается число попаданий в каждый из интервалов. Полученное таким образом число (количество случаев) и есть частота соответствующего интервала. Сумма всех частот интервалов равняется N, то есть общему числу случаев. Отношение частоты к общему числу случаев называется относительной частотой интервала (Таблица 1).

Пример: Результаты тестирования 14 учениковучеников 10 класса одной из школ Ленинградской области (по результатам ШТУР субтест: способность обобщения):

7; 10; 11; 11; 12; 13; 13; 14; 16; 16; 18; 18; 20; 25; 28.

Таблица 1

Способность обобщения учеников 10 класса

одной из школ Ленинградской области (по результатам ШТУР)

Вариант А	Вариант Б
Интервал квантования	Абсолютная частота	Относительная частота (%)	Интервал квантования	Абсолютная частота	Относительная частота (%)
[6 - 8]			[6-10]
[9 - 11]			[11-15]
[12-14]			[16-20]
[15-17]			[21-25]
[18-20]			[26-30]
[21-23]
[24-26]
[27-29]

На практике наиболее удобно, чтобы количество интервалов (столбцов) было не меньше 5, но не больше 15. Формировать интервалы можно различным образом, начиная либо с наименьшей, либо наибольшей величины, важно, чтобы расстояние между границами интервалов было одинаковым. При подготовке данных для построения гистограммы рекомендуется не ограничиваться лишь одной попыткой квантования: нередко изменение числа групп и границ интервалов помогает выявить скрытые неоднородности распределения случайной величины (рис.1).

Подсчитав частоту для каждого интервала, строим гистограмму. Чтобы подчеркнуть непрерывность изменения случайной величины, столбцы гистограммы следует располагать вплотную друг к другу. На оси «Х» графика принято обозначать или границы, или середины интервалов квантования. По оси «Y» указывается абсолютная частота. Результаты построения можно представить не только в виде столбчатой диаграммы, но также в виде полигона. На полигоне частот число испытуемых указывается точкой, расположенной над серединой интервала на высоте, соответствующей его частоте, а сами точки последовательно соединены прямолинейными отрезками (рис.2). Полигон по своему назначению полностью аналогичен гистограмме.

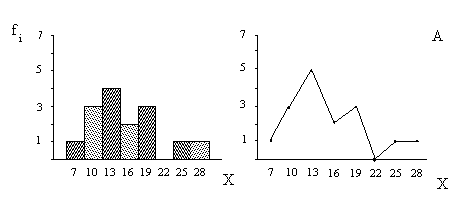
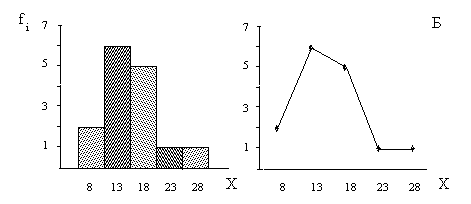
Рис. 2. Гистограмма (слева) и полигон распределения случайной величины (способности обобщения) по данным таблицы 1, с выделением 8 (А) и 5 (Б) интервалов квантования. По оси Х указаны середины интервалов.

При характеристике распределения некоторой непрерывной случайной величины число подразделений по горизонтальной шкале теоретически является бесконечным, а значение каждого интервала - бесконечно малым. В этом случае полигон частот примет вид кривой распределения частоты встречаемости случайной величины.

3.2 Параметры распределения

Распределение случайной величины характеризуется параметрами распределения, которые объединены в четыре группы характеристик:

· характеристики положения,

· характеристики рассеивания,

· характеристики асимметрии,

· характеристики эксцесса.

Естественно, что параметры распределения определяются только для данных, представленных либо в интервальной шкале, либо в шкале отношений.

Из характеристик положения рассмотрим моду, медиану и среднее арифметическое значение. По-другому эти параметры называются мерами центральной тенденции.

Мода (М₀) - наиболее часто встречающееся значение; его называют также модальным значением. Кроме модального значения используется также понятие модального интервала - так именуется интервал, куда попадает наибольшее количество значений. Нередко модальное значение оказывается как раз в модальном интервале. Распределение величины может быть унимодальным и полимодальным: если мода в распределении одна - то распределение унимодальное, если более - то полимодальное.

Среднее арифметическое значение М_х рассчитывается по формуле:

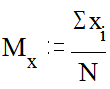
где Sх_i - это сумма всех значений случайной величины от первого х₁ до последнего x_N, а N - это общее число значений случайной величины.

Медиана (М_е) - это такое значение случайной величины, которое делит упорядоченную (в порядке возрастания или убывания величины) выборку пополам, то есть справа и слева от медианы находится равное количество значений случайной величины. При нечетном количестве измерений за медиану принимается непосредственно центральное значение, справа и слева от него располагается по (n-1)/2 значений. Так, в выборке из 15 упорядоченных значений это будет восьмое значение, а в выборке из 23 значений - двенадцатое и т.д.

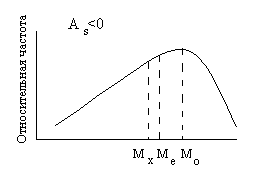
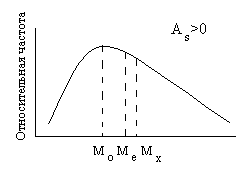
Рис.3. Соотношение между мерами центральной тенденции в асимметричном частотном распределении.

Если число значений случайной величины в выборке четное, то медиана оказывается между двумя значениями; в этом случае значение медианы рассчитывается как среднее между ними. На кривой распределения значение медианы всегда располагается между значениями моды и среднего арифметического (рис.3).

Квантили - это такие значения случайной величины, которые делят распределение на равные части. Есть несколько разновидностей квантилей:

· Квартили делят распределение на 4 равных части по 25%, соответственно квартилей три Q₁, Q₂, Q₃.

· Квинтили - их 4 (К₁....К₄), они делят распределение на 5 частей по 20% в каждой.

· Децили. Девять децилей (D₁... D₉) делят распределение на 10 частей по 10%.

· Процентили в количестве 99 (Р₁....Р₉₉) делят распределение на 100 частей по 1%.

Все остальные квантили можно выражать через процентили: так, первый квинтиль - это двадцатый процентиль или второй дециль. Второй квартиль - это 50 процентиль, или пятый дециль, или медиана.

Процентили нельзя ни в коем случае путать с процентными показателями. Процентные показатели - это первичные показатели, определяющие количество правильно выполненных заданий, а процентиль - показатель производный, указывающий на долю от общего числа членов группы. Первичный результат, который ниже любого показателя в выборке получает нулевой процентиль Р_о, а результат, превышающий все другие показатели группы - получает процентильный ранг 100 - Р₁₀₀. Эти процентили не означают ни нулевого, ни 100-процентного выполнения теста.

Среди характеристик рассеивания рассмотрим:

· размах d

· дисперсию s² или D

· среднеквадратическое (стандартное) отклонение s

· коэффициент вариации V.

Размах d - это разность между максимальным и минимальным значениями случайной величины:

d = х_max - х_min

Дисперсия s2 (или D) характеризует разброс значений случайной величины вокруг среднего арифметического значения, т.е. насколько плотно значения случайной величины группируются вокруг среднего арифметического Мх. Чем больше разброс, тем сильнее варьируют результаты испытуемых в данной группе, тем больше различия между испытуемыми.

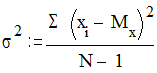
На первый взгляд может показаться, что было бы проще взять не квадрат значений отклонения от среднего, а просто отклонения значений от среднего. Но легко убедиться, что сумма таких отклонений будет равна нулю. Возведение же отклонений от среднего в квадрат позволяет избежать отрицательных чисел. На практике расчета дисперсии наряду с указанной формулой используется и расчет «способом моментов» по формуле

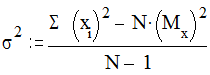
где S(x_i)² - сумма квадратов значений Х.

Дисперсия имеет «квадратную размерность», то есть, если какая-то величина измерена в сантиметрах, то размерность дисперсии - сантиметры в квадрате, а если в баллах - то дисперсия - в «баллах в квадрате». Это не всегда удобно, большую наглядность в отношении разброса величины имеет среднеквадратическое или стандартное отклонение s (греческая буква «сигма»). Размерность этого параметра совпадает с размерностью случайной величины.

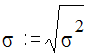
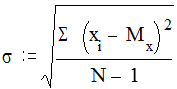
Среднеквадратическое отклонение используется очень широко в математической статистике. Малое значение стандартного отклонения указывает, что наблюдения хорошо группируются около среднего арифметического значения. Большое значение стандартного отклонения говорит о том, что наблюдения широко рассеяны относительно среднего значения и имеют слабую тенденцию к централизации.

Коэффициент вариации размерности не имеет, он служит для сравнения вариативности, то есть изменчивости случайных величин, имеющих различную природу. Рассчитывается коэффициент вариации по формуле:

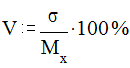
Если коэффициент вариации меньше 40%, то коэффициент вариации признается низким, то есть изменчивость величины невелика.

Характеристики асимметрии. В случаях, когда по тем или иным причинам более часто встречаются значения с показателями ниже или выше среднего, то появляются асимметричные распределения величины. Основная мера асимметрии - это коэффициент асимметрии A_s, рассчитываемый по формуле:

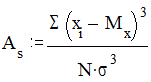
Коэффициент асимметрии изменяется от минус до плюс бесконечности. Асимметрия бывает левосторонняя или положительная, если A_s>0 (на рисунке 2 справа), и правосторонняя или отрицательная, если коэффициент асимметрии меньше 0 (слева на рис.2). При левосторонней асимметрии чаше встречаются значения по величине меньшие среднего арифметического (то есть медиана, и мода на графике находятся слева от среднего арифметического), при правосторонней асимметрии, соответственно, чаще встречаются значения, по величине превосходящие среднее арифметическое. Для симметричных распределений коэффициент асимметрии равен нулю, мода, медиана и среднее арифметическое совпадают между собой.

Характеристики эксцесса: Коэффициент эксцесса (или островершинности) рассчитывается по формуле

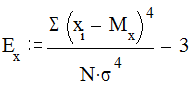
Распределения с острой вершиной будут характеризоваться положительным эксцессом, а сглаженные либо с понижением в центральной части - отрицательным. Пример расчета параметров распределения приведен в таблице 2:

Таблица 2

Дата добавления: 2014-12-27