
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дизъюнктивные и конъюнктивные нормальные формы. Полином Жегалкина. Двойственные и самодвойственные функции. 2 страница
|
|
|
|
 т.к.
т.к. 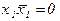
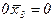


2)  3)
3) 
4) 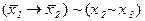 5)
5) 
2.3. Представить в виде полинома Жегалкина данную функцию:
1) 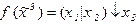
Решение: строим истинностную таблицу для данной функции

| 
| 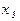
| 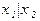
| 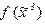
|
а) построим полином Жегалкина методом неопределенных коэффициентов
 - (1)
- (1)
стандартный вид полинома Жегалкина для функций от трех переменных.
В формулу (1) подставляем значения первой строчки переменных и получаем, что

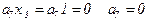



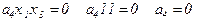
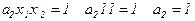

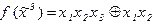
б) построим полином Жегалкина методом логических преобразований


в) построим полином Жегалкина составляя элементарные конъюнкции. Находим переменные, для которых значение функции равно 1 и составляем элементарные
конъюнкции. Соединяем их знаком 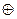 , затем используем свойства
, затем используем свойства  и
и


2) 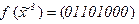 3)
3) 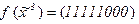 4)
4) 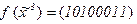
5)  6)
6) 
2.4. Построить полином Жегалкина методом логических преобразований:
1) 
2) 
3) 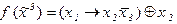
4) 
5) 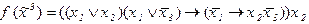
2.5. Является ли функция  двойственной к функции
двойственной к функции  , если:
, если:
1) 
Решение: по определению функция  двойственна к функции
двойственна к функции 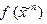 , если
, если
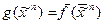 . Строим истинностную таблицу для функций
. Строим истинностную таблицу для функций
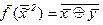 и
и  .
.

| 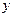
| 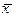
| 
| 
| 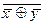
| 
|
Ответ: т.к.  , то функция
, то функция 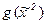 двойственна к функции
двойственна к функции  .
.
2) 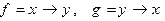 3)
3) 
4) 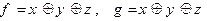 5)
5) 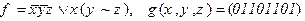
2.6. Пользуясь определением двойственности построить формулу, реализующую функ-
цию, двойственную к функции  . Полученное выражение упростить:
. Полученное выражение упростить:
1) 
Решение: по определению 
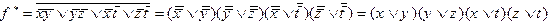
2) 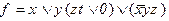
3) 
4) 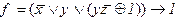
3. Линейные и монотонные функции. Функции, сохраняющие константу. Самодвойственные функции. Замкнутые классы и полные системы в  .
.
Опр 1. Функция  называется самодвойственной, если
называется самодвойственной, если  . Класс само-
. Класс само-
|
|
|
двойственных функций обозначается S.
Опр 2. Функция  называется линейной, если она представима в виде
называется линейной, если она представима в виде
 , где
, где  ,
,  . Множество всех линейных
. Множество всех линейных
функций обозначается L.
Опр 3. Говорят, что функция  сохраняет константу 0 (константу 1), если
сохраняет константу 0 (константу 1), если
 (
(  ). Множество функций, сохраняющих константу 0
). Множество функций, сохраняющих константу 0
или 1, обозначается соответственно  и
и 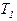 .
.
Опр 4. Булева функция  называется монотонной, если для любых двух наборов
называется монотонной, если для любых двух наборов 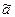 и
и
 из
из 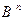 , таких, что
, таких, что  имеет место неравенство
имеет место неравенство  . В противном
. В противном
случае функция называется немонотонной. Класс монотонных функций обозна-
чается M.
Опр 5. Наборы 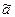 и
и  называются соседними, если они имеют вид:
называются соседними, если они имеют вид:


Опр 6. Пусть M - некоторое множество функций алгебры логики. Замыкание [M] мно-
жества M называется совокупностью всех функций из  , являющихся суперпо-
, являющихся суперпо-
зициями функций из множества M.
Опр 7. Множество M называется функционально замкнутым классом, если [M]=M.
Опр 8. Пусть M - замкнутый класс в  . Подмножество R из M называется функци-
. Подмножество R из M называется функци-
онально полной системой в M, если [R]=M.
Опр 9. Множество 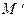 , содержащееся в замкнутом классе M (в т.ч. M=
, содержащееся в замкнутом классе M (в т.ч. M=  ) называется
) называется
полным классом в M, если оно не является полной системой в M, но для каждой
функции 
Опр 10. Система G называется независимой, если никакая функция  не представ-
не представ-
лена суперпозициями функций из  .
.
Опр 11. Независимая система G называется базисом функционально замкнутого класса
K, если всякая функция из K есть суперпозиция функций из G.
Теорема 1. Система полна в  , тогда и только тогда, когда она целиком не содержится
, тогда и только тогда, когда она целиком не содержится
ни в одном классе  ,
, 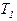 , S, L, M.
, S, L, M.
Теорема 2. Булева функция немонотонная, тогда и только тогда, когда существует, хотя
бы два соседних набора  , таких что
, таких что 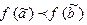
Лемма о немонотонной функции. Из немонотонной функции путём подстановок 0,1 и x можно получить функцию отрицания  .
.
Лемма о несамодвойственной функции. Из несамодвойственной функции, путём подстановки функций  , можно получить несамодвойственную функцию одной переменной, т.е. const 1 или 0.
, можно получить несамодвойственную функцию одной переменной, т.е. const 1 или 0.
|
|
|
Лемма о нелинейной функции. Из всякой нелинейной функции, путём подстановок 0, 1 и функций x, 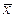 , а также, быть может, навешиванием отрицания над самой функцией, можно получить конъюнкцию
, а также, быть может, навешиванием отрицания над самой функцией, можно получить конъюнкцию  .
.
3.1. Разлагая функцию  в полином Жегалкина, выяснить является ли она линейной.
в полином Жегалкина, выяснить является ли она линейной.
1) 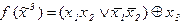 2)
2) 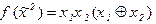
3) 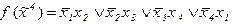 4)
4) 
3.2. Выяснить, является ли линейной функция  .
.
1)  2)
2) 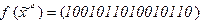
3)  4)
4) 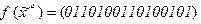
3.3. Самодвойственна ли функция  .
.
1) 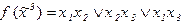
Решение: Алгоритм определения самодвойственности функции:
a) строится истинностная таблица
b) сравниваем симметричные наборы переменных. Если значения функции
на этих наборах не равны, то данная функция самодвойственна.

| 
| 
| 
| 
| 
| 
| 
|




Ответ: функция 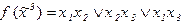 самодвойственна.
самодвойственна.
2) 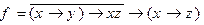 3)
3) 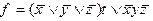
4)  5)
5) 
3.4. Из несамодвойственной функции  с помощью подстановки на места переменных функций
с помощью подстановки на места переменных функций  и
и 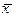 получить константу.
получить константу.
1) 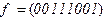 2)
2) 
3)  4)
4) 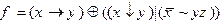
3.5. Какие из перечисленных ниже функций являются монотонными.
1) 
Решение:
a) строим истинностную таблицу для данной функции
| x | y | 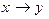
| 
|
b) согласно теореме 2, сравним значения функции для соседних наборов
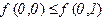

Ответ: функция  - монотонная.
- монотонная.
2)  3)
3) 
4)  5)
5) 
6) 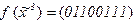 7)
7) 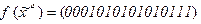
8) 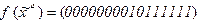
3.6. Перечислить все функции  , удовлетворяющие следующим условиям:
, удовлетворяющие следующим условиям:
1) 
2) 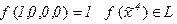
3.7. Показать, что если  , то
, то  .
.
3.8. Показать, что всякая монотонная функция содержится не менее чем в двух классах из
 .
.
3.9. Из немонотонной функции  с помощью подстановки на места переменных констант
с помощью подстановки на места переменных констант
0,1 и функции  получите функцию
получите функцию 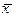 .
.
1)  2)
2) 
3) 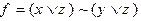 4)
4) 
5) 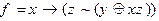 6)
6) 
3.10. Какие из следующих булевых функций сохраняют константу 0 (константу 1).
1)  2)
2)  3)
3)  4)
4) 
3.11. Используя критерий полноты, выяснить, полна ли в  система R.
система R.
1) 
Решение: Составляем истинностную таблицу для функций заданных в системе R.
| Таблица 1 | Таблица 2 | ||||||

| 
| 
| 
| 
| 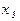
| 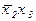
| 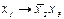
|
Определяем, к какому из замкнутых классов принадлежит данная функция, т.е.
|
|
|
составляем таблицу Поста.

| 
| 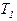
| L | M | S |

| - | + | - | - | - |
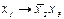
| - | - | - | - | - |
Ответ: система R - полна.
2)  3)
3) 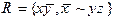
4)  5)
5) 
3.12. Какие из перечисленных систем зависимы. Укажите независимые системы.
1) 
Решение: 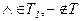

Ответ: система  независимая.
независимая.
2)  3)
3) 
3.13. Из системы  , полной для замкнутого класса
, полной для замкнутого класса  выделите базис.
выделите базис.
1) 
Решение: 
| f | 
| 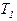
| M | S | L |
| + | - | + | - | + | |
| - | + | + | - | + | |

| + | + | + | + | + |
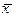
| - | - | - | + | + |

Ответ:  - базис для замкнутого класса M
- базис для замкнутого класса M
2)  3)
3) 
3.14. Пример №1. Пусть функция задана формулой 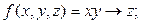
| x | y | z | f(x) |
Проверяем функцию на монотонность. Выписываем наборы переменных, где нарушается монотонность функции.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 726; Нарушение авторских прав?; Мы поможем в написании вашей работы!