Нечеткие множества

Записывая и решая задачу на языке исчисления высказываний или предикатов, мы получаем ответ в виде «да» или «нет»,(истина или ложь, 0 или 1). Однако во многих задачах мы не уверены в исходных данных, мы знаем их приближенно и поэтому удовлетворимся приближенным ответом.

Для математического решения таких задач используется нечеткая логика, предложенная американским математиком Л. Заде в начале 60-х годов.

Обычная логика, в которой есть два логических значения ИСТИНА и ЛОЖЬ, связана с таким же четким разделением объектов на два множества. Например, логическое условие

ПРИЗЫВНИК = ((ПОЛ = МУЖСКОЙ) Ù (ВОЗРАСТ>ПРИЗЫВНОЙ))

подразумевает разделение людей по признаку пола МУЖСКОЙ/ЖЕНСКИЙ и по возрасту ВОЗРАСТ>ПРИЗЫВНОЙ/ ВОЗРАСТ<ПРИЗЫВНОЙ. Логическая операция конъюнкции описывает ПРИЗЫВНИКА как пересечение множеств:

Рис.2.1.Операция пересечения множеств

Вместе с тем во многих случаях приходится иметь дело с не столь определенными понятиями. Например, выражение МОЛОДОЙ ЧЕЛОВЕК не указывает точно ни на какой возраст. Правда, можно отметить, что возраст 10 лет под понятие МОЛОДОГО ЧЕЛОВЕКА. по-видимому, не подпадает, точно так же, как и возраст 50 лет. Однако точно указать диапазон возраста МОЛОДОГО ЧЕЛОВЕКА в виде условия

МОЛОДОЙ ЧЕЛОВЕК=((ВОЗРАСТ>МИНИМАЛЬНЫЙ) И (ВОЗРАСТ< МАКСИМАЛЬНЫЙ)) невозможно – множество возрастов, подпадающих под понятие МОЛОДОГО ЧЕЛОВЕКА, является нечетким.

Если считать, что принадлежность объекта множеству описывается функцией принадлежности, принимающей значения от 0 до 1, то разница между обычными (четкими) и нечеткими множествами состоит в следующем. Для четкого множества функция принадлежности принимает значения только 0 и 1.

Например, функция принадлежности к призывному возрасту P (y) имеет вид (рис.2.2). В случае же нечеткого множества функция принадлежности принимает и промежуточные значения. Например, функция принадлежности к множеству МОЛОДОЙ ЧЕЛОВЕК может иметь вид (рис.2.3).

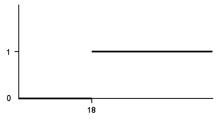Рис.2.2. Функция принадлежности четкого множества.

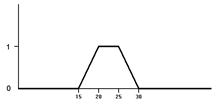Рис.2.3. Функция принадлежности нечеткого множества

и в таком случае описывается формулами:

при y <15 P (y)=0;

при 15< y <20 P (y)=(y -5)/5;

при 20< y <25 P (y) = 1;

при 25< y <30 P (y)=(30- y)/5;

при y >30 P (y) = 0.

Иными словами, при возрасте менее 15 и старше 30 лет человек молодым заведомо не является, а в промежутке от 20 до 25 лет - заведомо является. В промежутке от 15 до 20 лет статус МОЛОДОГО ЧЕЛОВЕКА плавно возрастает, принимая значения от 0 до 1, а в промежутке от 25 до 30 лет - убывает от 1 до 0.

Для того, чтобы описать нечеткое множество МОЛОДОЙ ЧЕЛОВЕК, следует указать все его элементы с указанием степени принадлежности элемента множеству. Это делается с помощью записи

МЧ=0.2/16+0.4/17+0.6/18+0.8/19+1/20+1/21+1/22+1/23+1/24+1/25+0.8/26+0.6/27+0.4/28+0.2/29

В тех случаях, когда это не может привести к путанице, можно использовать обычное обозначение коэффициентов, принятое в алгебре. Например, если множество Z состоит из элементов a, b, c, d, e с функцией принадлежности

Z = 0.1/ a +0.5/ b +0.9/ c +0.7/ d +0.5/ e

это может быть также записано во форме

Z = 0.1 a +0.5 b +0.9 c +0.7 d +0.5 e

2.2.1. Операции с нечеткими множествами.

К нечетким множествам, как и к четким, применимы операции объединения, пересечения и дополнения. Если считать, что в универсальном множестве U выделены два нечетких множества A и B с функциями принадлежности f и g, то их объединение имеет функцию принадлежности h

h (u) = max (f (u), g (u))

Например, если

U = (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)

A = 0.8/0+0.7/1+0.6/2+0.4/3+0.2/4+0.1/5+0.1/6+0.1/7

B = 0.1/3+0.3/5+0.5/7+0.7/8+0.9/9

то A È B имеет вид

A È B = 0.8/0+0.7/1+0.6/2+0.4/3+0.2/4+0.3/5+0.1/6+0.5/7+0.7/8+0.9/9

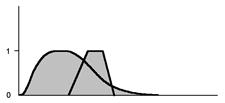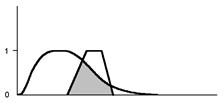
Аналогично, функция принадлежности для пересечения нечетких множеств A и B имеет вид min (f (u), g (u)). В том же примере

A Ç B = 0.1/3+0.1/5+0.1/7

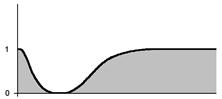
Дополнение множества имеет функцию принадлежности, вычисляемую как дополнение до 1 функции принадлежности исходного множества. Так, дополнение множества A имеет функцию принадлежности

Ø A = 0.2/0+0.3/1+0.4/2+0.6/3+0.8/4+0.9/5+0.9/6+0.9/7+1/8+1/9

Легко заметить, что если множества являются четкими, т.е. функция принадлежности принимает только значения 0 и 1, то построенные указанным образом функции принадлежности описывают обычные операции объединения, пересечения и дополнения множеств.

НЕЧЕТКАЯ ЛОГИКА

В отличие от обычной логики, где существуют только два значения истинности утверждения ИСТИНА и ЛОЖЬ, в нечеткой логике "значение истинности" утверждения может принимать и промежуточные значения. Считается, что ИСТИНА имеет значение 1, ЛОЖЬ - 0, и истинность любого утверждения u, обозначаемая m (u), находится в промежутке между этими значениями.

В нечеткой логике существуют те же логические операции конъюнкции, дизъюнкции и отрицания, однако они определяются иначе, чем в обычной логике. Если истинность логических операций конъюнкции, дизъюнкции и отрицания в обычной логике задается таблицами истинности, то в нечеткой логике она задается формулами. Если истинность утверждения u равна m (u), а v - m (v), то истинность конъюнкции, дизъюнкции и отрицания выражается формулами

m (u Ù v) = min (m (u), m (v)), m (u Ú v) = max (m (u), m (v))

m (Ø u) = 1- m (u)

При этом свойства нечетких операций в значительной степени сходны со свойствами операций в обычной логике, в частности:

m (u Ù v)= m (v Ù u), m (u Ú v)= m (v Ú u)

m ((u Ù v)Ù w)= m (u Ù(v Ù w)), m ((u Ú v)Ú w)= m (u Ú(v Ú w))

m (Ø(Ø u))= m (u), m (Ø(u Ù v))= m (Ø u ÚØ v)

m (Ø(u Ú v))= m (Ø u ÙØ v), m ((u Ú v)Ù w)= m ((u Ù w)Ú(v Ù w))

m ((u Ù v)Ú w)= m ((u Ú w) (v Ú w)), m (0Ú u)= m (u)

m (1Ú u)=1, m (0Ù u)=0, m (1Ù u)= m (u)

(Однако аналогия не является полной - например, аналоги формул u ÙØ u =0 и u ÚØ u =1 в нечеткой логике неверны.)

Используемые в логическом выводе формулы импликации вида A É B также могут быть нечеткими, т.е. их уровень истинности может быть меньше 1. В этом случае уровень истинности заключения вычисляется как произведение уровня истинности посылки на уровень истинности импликации. Например, если m (A)=0.9, а m (A É B) = 0.8, то m (B)=0.72.

Вопросы для самопроверки к главе 2:

1.Могут ли системы искусственного интеллекта создаваться на одном из алгоритмических языков, например Бейсике?

2.Каким образом на языке исчисления высказываний можно записать выражение «студент должен сдать экзамены по математике и физике или по литературе и истории»?

3.Может ли функция принадлежности быть равна 3?

4.Сколько функций трех переменных существует в исчислении высказываний?

5. Запишите функцию эквивалентности через функции конъюнкции, дизъюнкции и отрицания.

Тесты к главе 2

1.Исчисление высказываний оперирует

А) с троичными переменными, Б) с двоичными переменными,

В) с однозначными переменными.

2. Свойства исчисления высказываний доказываются с помощью

А) логического вывода,Б) таблиц истинности, В) формул.

3.Число логических функций

А) бесконечно, Б) конечно, но не зависит от числа аргументов

В) зависит от числа аргументов.

4.Логическое сложение двух единиц равно

А) нулю, Б) двум, В) единице.

5.Функция принадлежности объединения двух нечетких множеств равна

А) максимуму функции принадлежности каждого множества

Б) функции принадлежности одного из множеств

В) минимуму функции принадлежности каждого множества.

Глава 3. Логические рассуждения.

Рассуждением или умозаключением обычно называют ряд мыслей, изложенных в логически последовательной форме.

Агент должен уметь находить интересующие его состояния среды (целевые состояния), если он что-либо знает о других ее состояниях. Определение целевых состояний осуществляется с помощью поиска или рассуждений в пространстве состояний.

Дата добавления: 2014-12-27