
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Закон больших чисел и центральная предельная теорема
Структура общего решения линейного неоднородного дифференциального уравнения (ДУ). Метод Лагранжа. Построение частного решения неоднородного ДУ с постоянными коэффициентами при специальной правой части.
Вопрос 11.
- Структура общего решения линейного неоднородного ДУ (ЛНДУ).
Ly=f (1)
Полезными являются следующие свойства решений:
Теорема 1: Если у0 – решение однородного,
у* - решение неоднородного, то
у0 + у* - решение неоднородного.
Док-во: L(y0 + y*) = Ly0 + Ly* = 0 + f = f. ч.т.д.
Теорема 2: Если уi – решение уравнения Ly = fi (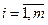 ), то
), то
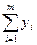 - решение уравнения вида
- решение уравнения вида  .
.
Док-во: 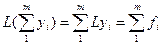 . ч.т.д.
. ч.т.д.
Основным результатом является следующая теорема:
Теорема 3: (о структуре общего решения ЛНДУ)
Справедлива следующая формула:
уо.н. = уо.о. + уч.н. (2)
где уо.н. – общее решение неоднородного;
уо.о. - общее решение однородного;
уч.н. - частное решение неоднородного.
Док-во: Исследуем (1). Замена:
у = уч.н. + z, z =?.
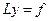 ~ L(yн.ч. + z)= f ~ Lyч.н. + Lz = f ~ f+Lz = f ~ Lz=0 ~ z=yо.о.
~ L(yн.ч. + z)= f ~ Lyч.н. + Lz = f ~ f+Lz = f ~ Lz=0 ~ z=yо.о.
Тогда:
у = уо.о. + уч.н. ~ yо.н. = уо.о. + уч.н.
ч.т.д.
- Метод Лагранжа (Метод вариации произвольных постоянных(МВПП)).
Замечание: В рамках этого метода предлагается условие, которое упрощает дальнейшие рассуждения. Для понимания смысла такого условия достаточно рассмотреть лишь уравнение 2-го порядка.
 (1)
(1)
где 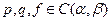 - известные функции
- известные функции
y = g(x) - искомая функция.
1) Предварительно решается соответствующее однородное уравнение: 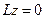 (2)
(2)
Пусть 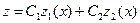 (3) - общее решение, причем {z1+z2} – ФСР уравнения (2).
(3) - общее решение, причем {z1+z2} – ФСР уравнения (2).
~  и:
и:
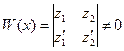
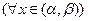
2) Согласно методу вариации произвольных постоянных (Лагранжа), решение уравнения (1) отыскивается в виде (3), в котором 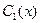 и
и 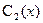 - новые неизвестные функции.
- новые неизвестные функции.
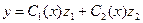 (4)
(4)
 и
и 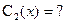
Следовательно нужно иметь 2 условия:
1-ое условие:  (5)
(5)

Идея метода: Во избежание 2-х производных 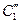 и
и  налагаем доп-ные условия:
налагаем доп-ные условия:
2-ое условие: 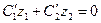 (6)
(6)

 подставляем в (1):
подставляем в (1):
 (7)
(7)
Относительно неизвестных 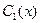 и
и 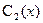 получим СЛАУ 2-го порядка:
получим СЛАУ 2-го порядка:
 (8)
(8)
Причем 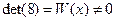
По теореме Крамера сущ-ет единственное решение:

Тогда:
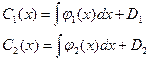
 , следовательно по (4) находим общее решение ур-я (1).
, следовательно по (4) находим общее решение ур-я (1).
- Построение частного решения ЛНДУ с постоянными коэффициентами при специальной правой части.
Зам: 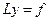

В силу доказанного, т.е. yо.н. = уо.о. + у*, основной задачей является построение

При специальной правой части  достаточно просто строится методом неопределенных коэффициентов (МНК).
достаточно просто строится методом неопределенных коэффициентов (МНК).
Под специальной правой частью будем понимать:
 где
где 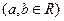
Pr, Ps – известные полиномы.
1) Решается характеристическое уравнение 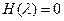
2) 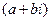 - проверяется на корень.
- проверяется на корень.
~ k – кратность корня 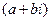
Вводится: 
Тогда  (9)
(9)
где  - полиномы степени m с неопределенными коэффициентами.
- полиномы степени m с неопределенными коэффициентами.
Неопределенные коэффициенты находим путем подстановки в формулу (9) данное неоднородное уравнение (1). При этом относительно них получается квадратная система линейных уравнений (как правило не полная система), которая имеет единственное решение.
Под законом больших чисел понимается ряд теорем, каждой из которых устанавливается факт сходимости средних арифметических большого числа случайных величин (СВ) к некоторым неслучайным величинам (НеСВ).
Основные формы закона больших чисел – теоремы Чебышева и Бернулли.
Теорема Чебышева: пусть 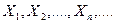 – последовательность независимых СВ, имеющих математические ожидания
– последовательность независимых СВ, имеющих математические ожидания  , дисперсии
, дисперсии  . Причем дисперсии ограничены одним и тем же числом
. Причем дисперсии ограничены одним и тем же числом  , т.е.
, т.е. 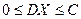 . Тогда для
. Тогда для 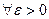 выполняется условие:
выполняется условие:
 или
или 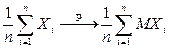 при
при  .
.
Таким образом, в теореме Чебышева утверждается, что среднее арифметическое СВ при большом числе слагаемых перестает быть СВ и может быть заменено НеСВ: средним арифметическим их математических ожиданий.
Следствие из Теоремы Чебышева: в частном случае независимых одинаково распределенных СВ 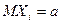 и
и 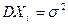 . Утверждение из Теоремы Чебышева приобретает вид:
. Утверждение из Теоремы Чебышева приобретает вид:
для 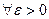
 или
или  при
при  .
.
В данном утверждении находит обоснование тот факт, почему в качестве истинного значения 
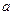 некоторой измеряемой величины используют среднее арифметическое отдельных измерений
некоторой измеряемой величины используют среднее арифметическое отдельных измерений 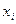 этой величины:
этой величины:  .
.
Согласно данному утверждению при больших  среднее арифметическое этих результатов отдельных измерений будет ближе к истинному значению, чем результат каждого отдельного измерения.
среднее арифметическое этих результатов отдельных измерений будет ближе к истинному значению, чем результат каждого отдельного измерения.
Кроме того, этот частный случай Теоремы Чебышева играет большую роль в математической статистике, являясь теоретическим обоснованием свойства состоятельности: 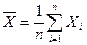 как оценки
как оценки 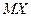 генеральной совокупности
генеральной совокупности 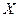 .
.
В основе доказательства Теоремы Чебышева лежит неравенство Чебышева и понятие сходимости последовательности СВ по вероятности.
Неравенство Чебышева: для каждой СВ 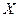 , имеющей конечную дисперсию
, имеющей конечную дисперсию 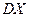 , при
, при 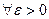 имеет место неравенство
имеет место неравенство  . Это неравенство позволяет оценить вероятности событий, зная только
. Это неравенство позволяет оценить вероятности событий, зная только 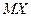 и
и 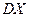 СВ
СВ 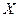 , не зная закона распределения, т.е. используя минимальную информацию.
, не зная закона распределения, т.е. используя минимальную информацию.
Замечание: если известен закон распределения с функцией распределения 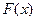 , тогда
, тогда 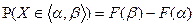 .
.
Последовательность СВ 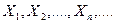 называется сходящейся по вероятности к некоторой величине
называется сходящейся по вероятности к некоторой величине  (которая является либо СВ, либо НеСВ), если для
(которая является либо СВ, либо НеСВ), если для 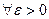 выполняется равенство:
выполняется равенство:  или
или 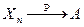 при
при  .
.
Сходимость по вероятности означает, что последовательность 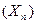 приближается к
приближается к  так, что отклонение члена последовательности
так, что отклонение члена последовательности  от
от  по абсолютной величине, превосходящее любое наперед заданное число
по абсолютной величине, превосходящее любое наперед заданное число  , становится все менее вероятным с увеличением
, становится все менее вероятным с увеличением  .
.
Для доказательства Теоремы Чебышева рассматривают СВ 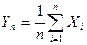 . В силу свойств математического ожидания и дисперсии конечного числа независимых СВ и условий Теоремы следует:
. В силу свойств математического ожидания и дисперсии конечного числа независимых СВ и условий Теоремы следует: 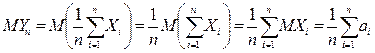 (
( , если
, если  равны).
равны).
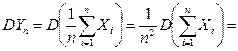 {для независимых СВ}
{для независимых СВ} 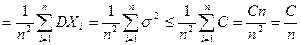
( для одинаково распределенных СВ)
для одинаково распределенных СВ)
Замечание: 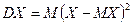 ,
, 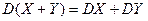 ,
,  .
.
Используя неравенство Чебышева, 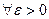 выполняется неравенство:
выполняется неравенство:


 ,
,
где 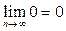 и
и 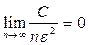
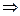
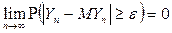 , что и требовалось доказать.
, что и требовалось доказать.
Частным случаем Теоремы Чебышева является Теоремы Бернулли (или закон больших чисел в форме Бернулли).
Теорема Бернулли: пусть в  независимых испытаниях по схеме Бернулли некоторое событие
независимых испытаниях по схеме Бернулли некоторое событие  в каждом из испытаний наступает с вероятностью
в каждом из испытаний наступает с вероятностью  . Тогда для
. Тогда для 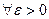 выполняется:
выполняется:
 , где
, где 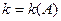 - число успехов или появлений события
- число успехов или появлений события  в
в  испытаниях,
испытаниях, 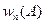 - относительная частота.
- относительная частота.
Утверждение Теоремы: 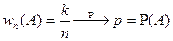 при
при  .
.
Доказательство Теоремы Бернулли следует из Теоремы Чебышева, если  ,
,
 0 0
| |
| 1-p | p |
где
Утверждение Теоремы Бернулли является теоретическим обоснованием статистического определения вероятности, тогда в качестве приближенного значения вероятности некоторого события 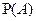 принимают частоту его появлений, в которых данное событие появляется. Теорема Бернулли является теоретическим обоснованием состоятельности
принимают частоту его появлений, в которых данное событие появляется. Теорема Бернулли является теоретическим обоснованием состоятельности  .
.
В Центральной Предельной Теореме (ЦПТ) исследуется вопрос возникновения нормального распределения как предельного для суммы большого числа СВ. Данная Теорема выявляет ту особую роль, которую играет нормальное распределение на практике. Нормальный закон всегда имеет место, когда СВ является результатом действия большого числа равномерно малых по их влиянию на весь результат случайных факторов, действующих независимо друг от друга.
Для случая одинаково распределенных независимых слагаемых:
ЦПТ: пусть 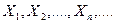 - последовательность независимых одинаково распределенных СВ, имеющих
- последовательность независимых одинаково распределенных СВ, имеющих 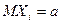 и
и 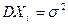 . Тогда функция распределения
. Тогда функция распределения  стандартизированной СВ
стандартизированной СВ  для
для  фиксированного
фиксированного 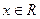 при
при  стремится к функции распределения
стремится к функции распределения  нормальной стандартной величины
нормальной стандартной величины 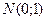 :
: 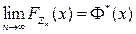 для
для  .
.
Величину 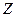 называют стандартизированной, если
называют стандартизированной, если  и
и 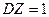 .
.
В ЦПТ используется понятие сходимости последовательности функции распределения или слабой сходимости.
Сходимость называется сходимостью последовательности функции распределения  к функции распределения
к функции распределения 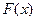 или слабой сходимостью последовательности СВ
или слабой сходимостью последовательности СВ 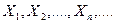 к СВ
к СВ 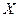 :
:  для слабой сходимости.
для слабой сходимости.
13. Регрессионный анализ: линейная и нелинейная регрессия, статистические свойства оценок коэффициентов регрессии.
Во многих прикладных задачах требуется построить математическую модель (уравнение), связывающую факторные (- изменение этих переменных влечет изменение результативной переменной) переменные Х1, …Хк и результативную (зависимую) переменную У. Предполагается У - случайной величиной, а Х1, …Хk не случайные величины. В этом случае математическая модель связи: Y=f (Х1…Хk) + ε(Х1…Хk) (1) (1) называется статистической моделью связи. где ε(Х1…Хk) – случайная величина при каждом наборе (x1,…xk), f(x)=M(Y|X=x) – функция регрессии, Если факторных переменных больше 2х, то говорят о множественной регрессионной модели, если факторная переменная 1,то – о парной регрессионной модели: Y=f (Х) + ε(Х) Основные свойства регрессионной модели состоят в том, что для каждого набора 1) 2) 3) Основные задачи регрессионного анализа: 1) установление модели регрессии, т.е. вида f( 2) нахождение оценок неизвестных параметров 3) проверка статистических гипотез о регрессии: гипотез об адекватности полученного уравнения Различают парную линейную и нелинейную регрессию. Линейной регрессией называют регрессию вида Нелинейные регрессии делятся на регрессии: 1. линейные по оцениваемым параметрам, но нелинейные по факторным переменным, например a) b) c) 2. нелинейные по оцениваемым параметрам факторным. параметрам a) b) Для оценки параметров уравнения регрессии линейных по параметрам Рассмотрим нахождение МНК оценок для парной линейной регрессии, имеющей вид: Согласно методу МНК Нормальная система МНК будет иметь вид: Выражая через линейный коэффициент корреляции (-1<r<1, если r=+(-)1, то СВ Х и У находятся в линейной зависимости) Возникает вопрос: как соотносятся 14. Проверка гипотез. Критерий χ2. Ошибки 1-го и 2-го рода. Лемма Неймана-Пирсона. Статистической гипотезой называют любое высказывание относительно свойств генеральной совокупности (ГС), проверяемой с помощью выборочных данных. Примерами гипотез являются: 1. гипотеза о равенстве математических ожиданий двух генеральных совокупностей (она возникает, например, когда нужно проверить одинаково ли среднее значение основных параметров изделий, производимых двумя станками, цехами) 2. гипотеза о равенстве дисперсий, когда следует сравнить точность двух измерительных приборов для измерения одной и той же величины) 3. гипотеза об однородности выборок (возникают в тех случаях, когда несколько малых выборок объединяются в одну большую и требуется до их объединения установить взяты они из одной генеральной совокупности или нет, если гипотеза подтверждается, то выборки можно объединить, иначе - нет) 4. гипотеза о законе распределения ГС (возникает в результате проведенной предварительной обработки данных (разведочного анализа), изучения гистограмм, полигона, значений выборочных коэффициентов ассиметрии) Статистические гипотезы бывают ü параметрическими ü не параметрическими Статистические гипотезы относительно неизвестных значений параметров распределения называют параметрическими, все другие гипотезы называются непараметрическими. Статистическую гипотезу называют простой, если она однозначно определяет распределение генеральной совокупности, в противном случае – сложной. Если неизвестный параметр Ө принимает одно возможное значение из своих возможных значений (параметрического пространства Проверяемую гипотезу H0 называют основной, наряду с ней рассматривают одну из альтернативных гипотез H1, противоречащих основной, например, если проверяется гипотеза H0: Ө=Ө0, то альтернативными будут H1: Ө<Ө0, Ө>Ө0, Ө ≠ Ө0. Выбор альтернативной гипотезы осуществляется конкретной постановкой задач. Критерием проверки статистической гипотезы (К) называют правило, по которому принимают решение принять или отклонить основную гипотезу. Критерий задают с помощью критического множества (множество, попадание в которое выборки ü если конкретная выборка ü 2) если При использовании любого критерия возможны ошибки 1-го и 2-го рода. Ошибка 1-го рода – отклонить верную основную гипотезу. Ошибка 2-го рода – это принять неверную основную гипотезу H0. Вероятность α совершить ошибку первого рода вычисляют по формуле: α(Ө)=P( Число α такое, что вероятность ошибки первого рода не превосходит его α(Ө)≤α называется уровнем значимости критерия К. В случае простой гипотезы уровень значимости полагают равным вероятности ошибки первого рода. А величину (1-β(Ө))=m(Ө) называют мощностью критерия. Наиболее мощный критерий при заданном уровне значимости принято называть оптимальным критерием. Одновременно минимизировать α(Ө) и β(Ө) при заданном объеме выборки n нельзя, т.к.при уменьшении одной вероятности, увеличивается другая. При построении критерия для проверки параметрических гипотез, как правило, стараются максимизировать его мощность (min вероятность ошибки второго рода), при фиксированном значении вероятности α ошибки первого рода. Построение оптимального критерия для проверки простых гипотез H0: Ө = Ө0, H1: Ө = Ө1 осуществляют на основании следующей леммы.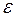 - погрешность модели (случайная переменная), порожденная или действием неучтенных факторов, или случайными ошибками измерений случайной величины У.
- погрешность модели (случайная переменная), порожденная или действием неучтенных факторов, или случайными ошибками измерений случайной величины У. :
: математическое ожидание случайных ошибок (отсутствие систематической погрешности)
математическое ожидание случайных ошибок (отсутствие систематической погрешности) i≠j случайные ошибки некоррелируемы
i≠j случайные ошибки некоррелируемы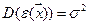 случайные ошибки имеют одинаковую дисперсию (гомоскедастичность - равноизменчивость)
случайные ошибки имеют одинаковую дисперсию (гомоскедастичность - равноизменчивость)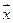 ), что заключает в себе предположение о зависимости функции регрессии от значений факторных переменных и неизвестных параметров (b1…bm)=
), что заключает в себе предположение о зависимости функции регрессии от значений факторных переменных и неизвестных параметров (b1…bm)=  .
. методом наименьших квадрат (МНК)
методом наименьших квадрат (МНК)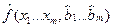 , о значимости найденных по выборке параметров.
, о значимости найденных по выборке параметров.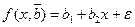 .
.

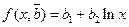
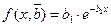

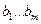 используют МНК. Согласно МНК в качестве оценок
используют МНК. Согласно МНК в качестве оценок 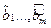 неизвестных параметров выбирают такие, для которых сумма квадратов невязок
неизвестных параметров выбирают такие, для которых сумма квадратов невязок  , т.е. функция S(
, т.е. функция S( )=
)= 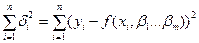 принимала бы наименьшее значение, т.е. S (
принимала бы наименьшее значение, т.е. S (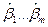 )=
)= 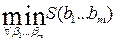 .
.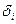 - отклонение факторного значения yi от теоретического
- отклонение факторного значения yi от теоретического  , рассчитанных по функциям регрессии
, рассчитанных по функциям регрессии 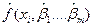 . Необходимым условием экстремума функции S является условие равенства частных производных 0
. Необходимым условием экстремума функции S является условие равенства частных производных 0 - нормальная система МНК
- нормальная система МНК .
. . Необходимые условия экстремума имеют вид:
. Необходимые условия экстремума имеют вид:  ,
, 


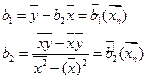

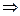
 ,
, 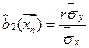 . Тогда выборочное уравнение парной линейной регрессии
. Тогда выборочное уравнение парной линейной регрессии 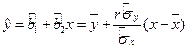 .
. с
с 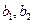 ? Оказывается для линейной регрессии
? Оказывается для линейной регрессии  при выполнении основных предположений 1)-3) регрессионного анализа - за оценки
при выполнении основных предположений 1)-3) регрессионного анализа - за оценки  , получаемые по МНК, являются несмещенными (математическое ожидание равно оцениваемому параметру), состоятельными (при увеличении объема выборки точечная оценка по вероятности стремится к оцениваемому параметру) и эффективными (имеющие наименьшую дисперсию в классе всех линейных несмещенных оценок). Если предположить, что ошибки наблюдений имеют нормальный закон распределений εi ~
, получаемые по МНК, являются несмещенными (математическое ожидание равно оцениваемому параметру), состоятельными (при увеличении объема выборки точечная оценка по вероятности стремится к оцениваемому параметру) и эффективными (имеющие наименьшую дисперсию в классе всех линейных несмещенных оценок). Если предположить, что ошибки наблюдений имеют нормальный закон распределений εi ~  , то оценки
, то оценки 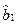 и
и  имеют также нормальное распределение, что позволяет легко строить для параметра
имеют также нормальное распределение, что позволяет легко строить для параметра 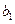 и
и  доверительные интервалы и тем самым определять погрешность оценивания.
доверительные интервалы и тем самым определять погрешность оценивания.
 ), то гипотезу называют простой, если принимает несколько значений, то называют сложной.
), то гипотезу называют простой, если принимает несколько значений, то называют сложной.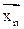 приводит к отклонению H0): W
приводит к отклонению H0): W  χn, где χn – выборочное пространство (совокупность всех возможных конкретных выборок из генеральной совокупности). Принимается решение на основе конкретной выборки следующим образом:
χn, где χn – выборочное пространство (совокупность всех возможных конкретных выборок из генеральной совокупности). Принимается решение на основе конкретной выборки следующим образом: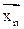
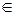 W(критическому множеству), то H0 отклоняется в пользу альтернативной;
W(критическому множеству), то H0 отклоняется в пользу альтернативной;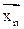 не принадлежит W, то принимается гипотеза H0 и отклоняется гипотеза H1 (гипотеза H0 при этом считается непротиворечивой данной выборке).
не принадлежит W, то принимается гипотеза H0 и отклоняется гипотеза H1 (гипотеза H0 при этом считается непротиворечивой данной выборке).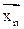
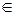 W│H0). Вероятность β совершить ошибку второго рода вычисляют по формуле: β(Ө)=P(
W│H0). Вероятность β совершить ошибку второго рода вычисляют по формуле: β(Ө)=P(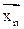
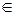
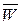 │H1), где
│H1), где 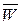 = χn \ W – множество принятия основной гипотезы.
= χn \ W – множество принятия основной гипотезы.
|
|
Дата добавления: 2015-01-03; Просмотров: 526; Нарушение авторских прав?; Мы поможем в написании вашей работы!