Надо знать, можно не писать

Случайной выборкой называют упорядоченную последовательность случайных величин X₁,..., X_n, каждая из которых имеет тот же закон распределения, что и генеральная совокупность (X₁, X₂,..., X_n)= .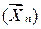

Генеральной совокупностью в математической статистике называют совокупность всех подлежащих обследованию объектов. Любое возможное значение случайной выборки называют реализацией случайной выборки или выборкой из генеральной совокупности X. Множество возможных значений случайной выборки называют выборочным пространством X_n ≤ Rⁿ.

Статистикой в мат. статистике называют любую функцию случайной выборки y(x₁,x₂,..,x_n).

Распределение статистики как случайной величины называют выборочным распределением, а значение на конкретной выборке y(x₁, x₂,…, x_n) называют выборочным значением.

Одна из основных задач мат. статистики – оценка неизвестных параметров распределения (скалярного Ө (тетта) или векторного ), характеризующих распределение генеральной совокупности. Задача возникает в тех случаях, когда распределение генеральной совокупности, задаваемое, например, функцией распределения, известно с точностью до данного параметра. Пусть распределение известно с точностью до скалярного параметра Ө, тогда

точечной оценкой параметра Ө называют статистику , значение которой на данной выборке (x₁, x₂,…, x_n) = 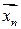и принимают за приближенное значение параметра Ө, т.е. .

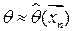Одним из наиболее универсальных методов оценивания параметров является метод максимального правдоподобия (предложен Фишером).

Оценкой метода максимального правдоподобия параметра Ө называют статистику, значение которой для любой конкретной выборки 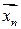удовлетворяет условию 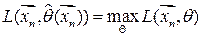, где 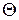- множество всевозможных значений параметра , - функция правдоподобия выборки .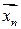

Функция правдоподобия имеет вид для

ü дискретной случайной величины

ü непрерывной случайной величины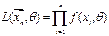

её величина считается мерой Ө для данной выборки .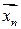

Если функция L (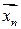, Ө) дифференцируема, как функция аргумента Ө для любой конкретной выборки и максимум ее достигается во внутренней точке множества 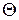, то данная точка 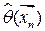будет являться точкой возможного локального экстремума и может быть найдена из необходимого условия локального экстремума путем решения уравнения (системы уравнений, если ):

Нахождение значения оценки 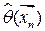существенно упрощается, если максимизировать не саму функцию правдоподобия, а ее логарифм, т.к. при логарифмировании точки экстремума остаются теми же, а уравнение упрощается.

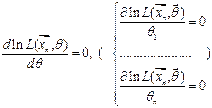
полученное уравнение (систему уравнений) называют уравнением (системой уравнений) метода максимального правдоподобия.

Найдем этим методом оценки неизвестных параметров для нормального закона распределения X~N(a,σ).

1. составим функцию правдоподобия

2. прологарифмируем

3. составляем систему уравнений максимального правдоподобия

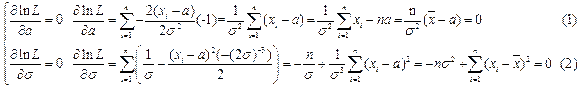
Таким образом, оценками правдоподобия и

Недостаток точечных оценок в том, что на конкретных выборках они не позволяют судить о степени близости 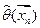и θ

Погрешность оценки позволяет охарактеризовать интервальное оценивание

Пусть распределение генеральной совокупности Х известно и задается функция распределения с точностью до скалярного параметра Ө (F(x, Ө))

Интервальной оценкой (доверительным интервалом) неизвестного параметра Ө называют случайный интервал 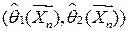, который накрывает истинное значение параметра Ө с заданной доверительной вероятностью (0<γ< 1), т.е.

Число γ называют доверительной вероятностью γ=1-α, где α – уровень значимости (обычные значения 0,9; 0,95; 0,99)

Точность интервальной оценки характеризуется длиной интервала , которая зависит от объема интервала n и доверительной вероятности γ: на конкретной выборке 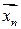при увеличении объема выборки и уменьшении γ, длина интервала будет уменьшаться и наоборот. Чем меньше длина интервала, тем точнее оценка и наоборот.

Доверительный интервал симметричен относительно точечной оценки:

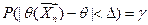, характеризует отклонение выборочного значения от его истинного значения и называется предельной ошибкой выборки. Доверительный интервал часто строят из предположения, что генеральная совокупность имеет нормальное распределение.

Общий метод построения доверительного интервала состоит в следующем:

пусть известна статистика, она зависит от 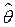и () называемая центральной статистикой со следующими свойствами:

ü ее функция распределения F_U(x) известна и не зависит от оцениваемого параметра .

ü функция U является непрерывной и строго монотонна по , тогда метод построения такого интервала называют методом статистики.

Для построения доверительного интервала поступают так: задают значение α – риск оценки и строят интервал так, чтобы дополнительные интервалы, дополняющие данный до области возможных значений параметра накрывали равновероятно с вероятностью (например, если Θ(-∞;+∞), то дополнительные интервалы (-∞; 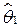), ( +∞)). Для этого находят критические точки распределения центральной статистики U, для которых выполняются условия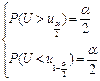

При этом вероятность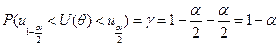

Если центральная статистика монотонно убывает по параметру , то неравенство будет равносильно нахождению обратной функции

где U^-1- обратная к U функция, тогда

Найдем методом центральных статистик доверительный интервал для параметров гауссовского распределения a(-∞;+∞), σ >0.

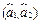=? (при условии σ неизвестно)

Используют в качестве центральной статистики – статистику Стьюдента , где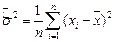

1) она имеет распределение Стьюдента

2) монотонно убывает по а

3) строим дополнительные интервалы (-∞; ), ( +∞)), которые накрывают истинное значение а с малой вероятностью и .

4) для нахождения границ доверительных интервалов поступают так: находят критические точки распределения Стьюдента: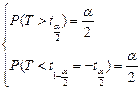

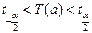
Строим обратную функцию к T(a):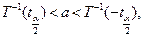

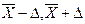=(), где =

Для построения доверительного интервала для параметра σ² используется центральная статистика 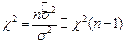, где n-число степеней свободы (- число независимых элементов выборки, не связанных между собой никакими отношениями) случайной выборки, если компоненты выборки связаны, то число степеней свободы уменьшается на число связей.

1) она монотонно убывает по σ² (0; +∞)

2) строим дополнительные интервалы (-∞; ), ( +∞)).

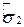3)

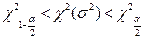
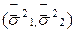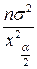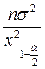=(, ). Этот метод можно применять для выборок любого объема

Дата добавления: 2015-01-03