Для самостоятельной работы 1 страница

ЗАДАЧИ И УПРАЖНЕНИЯ

(ПО ТЕМАМ 4 И 5)

Задача 1

На конец октября 2010 г. в РФ имелось следующее распределе­ние безработных по возрастным группам:

Возрастные группы, лет	Численность безработных, % к итогу
16−19	10,2
20−24	17,9
25−29	12,7
30−49	48,8
50−54	4,0
55−59	4,5
60−72	1,9
Всего	100,0

По данным распределения определить:

1) средний (арифметический) возраст безработных;

2) модальный возраст (моду);

3) медианный возраст (медиану);

4) среднее квадратическое отклонение;

5) коэффициент вариации.

Ответ: 1) 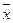= 34,3 года; 2) Мо = 22,4 года; 3) Me = 33,6 года; 4) = 11,5 года; 5) V =33,5%.

Задача 2

Имеются следующие данные за 2009 и 2010 гг. по РФ об урожайности, посевных площадях и валовом сборе пшеницы (озимой и яровой).

Культура	Урожай­ность, ц/га	Посевная площадь, млн,га	Урожай­ность, ц/га	Валовый сбор, млн. ц
Пшеница озимая Пшеница яровая	16,9 10,3	8,2 15,8	17,9 11,0

Определить среднюю урожайность пшеницы: а) в 2009 г. и б) в 2010 г.

Ответ: а) 12,555 ц/гa; б) 13,48 ц/га.

Задача 3

По данным таблицы «б» из задачи 3 темы 2 определить средний возраст безработных в 2010 г.:

а) мужчин; б) женщин.

Ответ: а) 35,5 года; б) 33,8 года.

Задача 4

По тем же данным (таблица «б» из задачи 3 темы 2) определить:

модальный возраст (моду) для мужчин и женщин;

медианный возраст (медиану) для мужчин и женщин.

Ответ:1) Мо мужчин = 22,6 года и Мо женщин = 22 года;

2) Ме мужчин = 35 лет и Ме женщин = 33,3 года.

Задача 5

Имеются следующие данные о распределении населения Мос­ковской области по уровню среднемесячного душевого дохода в 2009 г.

Среднемесячный душевой доход, тыс. руб.	Численность населения, % к итогу
До 200	15,3
200−400	50,6
400−600	23;5
600−800	7,3
800−1000	2.2
Свыше 1000	1,1

Определить в данном распределении:

1) среднемесячный душевой доход по области в целом;

2) моду;

3) медиану;

4) среднее квадратическое откло­нение доходов;

5) децильный коэффициент дифференциации (ДКД) доходов;

6) коэффициент Джини (G).

Ответ 1) 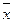= 367,6 тыс. руб.; 2) Мо = 313,1 тыс. руб.; 3) Me = 337,2 тыс. руб.;

4) 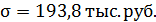; 5) ДКД = 4,7 раза; 6) G = 0,265.

Задача 6

Распределение населения Москвы по уровню среднемесячного в 2009 г. характеризовалось следующими данными.

Среднемесячный душевой доход, тыс. руб.	Численность населения, % к итогу
До 200	5,6
200−400	21,1
400−600	17,0
600−800	10,1
800−1000	6,1
Свыше 1000	40,1

Определить:

1) среднедушевой денежный доход на основе среднеарифметической моды и медианы;

2) дисперсию, среднее квадратическое отклонение, коэффициент вариации;

3) децильный коэффициент дифференциации доходов, ДКД;

4) коэффициент Джинни (показатель концентрации доходов),G.

Ответ: 1) 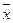= 720,6 тыс. руб., Мо = 1091,8. руб.; Ме = 724,7 тыс. руб.; 2) 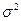= 126405,6;

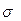= 356 тыс. руб.; V= 49,4%; 3) ДКД = 4,8 раза; 4) G = 0,272.

Задача 7

Имеются следующие данные о распределении населения Санкт-Петербурга по уровню среднемесячного душевого дохода в 2009 г.

Среднемесячный душевой доход, тыс. руб.	Численность населения, % к итогу
До 200	10,9
200−400	30,0
400−600	22,9
600−800	14,0
800−1000	8,3
Свыше 1000	13,9

Определить:

1) среднемесячный душевой доход в целом, по городу;

2) моду и медиану (по формулам и графически);

3) коэффициент вариации доходов;

4) ДКД населения по доходам;

5) степень концентрации доходов по группам (с помощью G).

6) построить кривую Лоренца.

По результатам анализа сделать выводы.

Ответ:1) 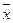= 541 тыс. руб.; 2) Мо = 345,8 тыс. руб.; Me = 479,5 тыс. руб.;

3) V= 57,5%; 4) ДКД = 5,75 раза; 5) G = 0,265.

Задача 8

По переписи населения 1926 г. в России доля грамотных среди женщин составляла 46%, а среди мужчин 77%. Определить общий (средний) процент грамотности всего населения и дисперсию этого показателя, если женщины составляли 53% в общей численности населения.

Ответ: 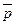= 60,57% (0,6057); 2) 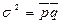= 0,2388.

Задача 9

В коллективных хозяйствах района средняя урожайность зерно­вых составила 19 ц/га при среднем квадратическом отклонении 3 ц/га, а в фермерских хозяйствах — соответственно 26 ц/га и 4 ц/га.

Определить:

1) среднюю урожайность зерновых по району, если известно, что посевная площадь под зерновыми в коллективных хо­зяйствах в 9 раз превышает площадь фермерских хозяйств;

2) общую дисперсию и среднее квадратическое отклонение уро­жайности зерновых в районе (по правилу сложения диспер­сии).

Ответ: 1) 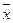= 19,7 ц/га; 2) 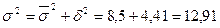; ц/га.

Задача 10

Для изучения уровня заработной платы рабочих на предприя­тии выборочно обследованы 500 мужчин и 300 женщин. Результаты исследования показали, что у мужчин средняя заработная плата со­ставила 1200 руб. при среднем квадратическом отклонении 200 руб., а у женщин — соответственно 800 руб. и 150 руб.

Определить:

1) общую среднюю заработную плату рабочих на заводе;

2) среднюю из групповых дисперсий;

3) межгрупповую дисперсию;

4) общую дисперсию зарплаты;

5) коэффициент вариации зарплаты на предприятии.

Ответ: 1) 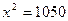руб.; 2) ; 3) ; 4) 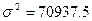; 5) V = 25,4%.

Тема 6

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ

При исследовании социально-экономических явлений часто приходится иметь дело со взаимосвязанными показателями. При этом часто связь, существующая между двумя или несколькими по­казателями, затушевывается, усложняется наслоением действия дру­гих причин (факторов). Изучить, насколько изменение одного пока­зателя зависит от изменения другого (или нескольких), — одна из важнейших задач статистики.

Следует различать функциональные и корреляционные связи. В отличие от функциональной зависимости, при которой каждому значению одной переменной строго соответствует одно определен­ное значение другой переменной, зависимость, при которой одному значению переменной (х) может соответствовать (в силу наслоения действия других причин) множество значений другой переменной (у), называют корреляционной. Корреляционная зависимость прояв­ляется лишь на основе массового наблюдения.

Примером корреляционной зависимости может служить зави­симость производительности труда от стажа работы рабочих, зависи­мость урожайности от срока сева, зависимость годового удоя коров от количества отелов и т. п.

Наиболее простым случаем корреляционной зависимости явля­ется парная корреляция, т.е. зависимость между двумя признаками (результативным и одним из факторных).

Основными задачами при изучении корреляционных зависимо­стей являются: 1) отыскание математической формулы, которая бы

выражала эту зависимость у от х; 2) измерение тесноты такой зави­симости.

Решение первой задачи, т.е. определение формы связи с после­дующим отысканием параметров уравнения, называется нахождени­ем уравнения связи (уравнения регрессии). Показатели, рассматри­ваемые как функция х, обозначают (читается: «игрек, выравнен­ный по икс»).

Возможны различные формы связи:

1) прямолинейная:

;

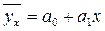2) криволинейная в виде:

а) параболы второго порядка

(или высших порядков);

б) гиперболы

;

в) показательной функции

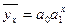и т. д.

Параметры для всех уравнений связи чаще всего определяют из так называемой системы нормальных уравнений, отвечающих требованию «метода наименьших квадратов» (МНК). Это требование можно записать как 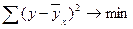или, при линейной зависимости,

,

,требуется определить, при каких значениях параметров 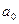и 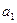сумма квадратов отклонений y от будет минимальной. Найдя частные производные указанной сум­мы по 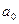и 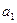и приравняв их к нулю, легко записать систему урав­нений, решение которой и дает параметры искомой функции, т. е. уравнения регрессии.

Так, система нормальных уравнений при линейной зависимос­ти имеет вид

.

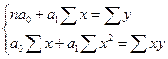Если связь выражена параболой второго порядка

,

то система нормальных уравнений для отыскания параметров 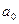, , 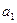выглядит следующим образом:

.

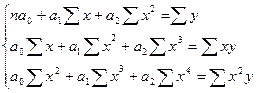Вторая задача — измерение тесноты зависимости — для всех форм связи может быть решена с помощью исчисления теоретичес­кого корреляционного отношения ():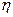

,

где 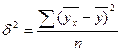- дисперсия в ряду выравненных значений результативного показателя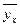

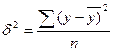- дисперсия в ряду фактических значений у.

Так как дисперсия 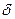² отражает вариацию в ряду только за счет вариации фактора х, а дисперсия ² отражает вариацию у за счет всех факторов, то их отношение, именуемое теоретическим коэффи­циентом детерминации, показывает, какой удельный вес в общей дис­персии ряда у занимает дисперсия, вызываемая вариацией факто­ра х. Квадратный корень из отношения этих дисперсий дает нам те­оретическое корреляционное отношение. Если 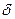² = ², то это озна­чает, что роль других факторов в вариации у сведена на нет, и отно­шение означает полную зависимость вариации у от х. Если ² = 0, то это означает, что вариация x никак не влияет на вариацию у, и в этом случае 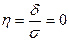. Следовательно, максимальное зна­чение, которое может принимать корреляционное отношение, рав­но 1, минимальное значение - 0.

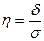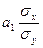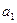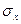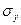Математически легко доказывается, что в случае линейной зависимости корреляционное отношение может быть заменено выражением , которое называют линейным коэффициентом корреляции и обозначают r, здесь — коэффициент регрессии в уравне­нии связи, и — соответственно среднее квадратическое откло­нение в ряду х и в ряду у.

Линейный коэффициент корреляции можно выразить и други­ми формулами, тождественными первой, в частности:

; ;

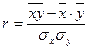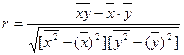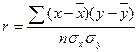
или

,

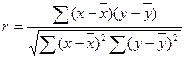а также

.

Линейный коэффициент корреляции может принимать по мо­дулю значения от 0 до 1 (знак «+» при прямой зависимости и знак «—» при обратной зависимости).

Рассмотрим решение некоторых задач по этой теме.

Задача 6.1

Пусть по 10 однотипным предприятиям имеются следующие данные о выпуске продукции (х) в тыс. ед. и о расходе условного топлива (у) в тоннах (графы 1 и 2 таблицы).

Требуется найти уравнение зависимости расхода топлива от выпуска продукции (или уравнение регрессии у по x) и измерить тесноту зависимости между ними.

Решение.

А. Рассматривая уравнение регрессии в форме линейной функ­ции вида , параметры данного уравнения (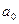 и 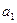) най­дем из системы нормальных уравнений

,

x	y	x	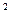xy	ух = 1,16 + 0,547х	y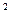
				3,9
				4,4
				5,5
				5,5
				6,6
				6,6
				8,8
				12,1
				12,1
				14,3

а необходимые для решения суммы , , , 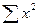рассчитаны выше в таблице. Подставляем их в уравнение и решаем систему:

,

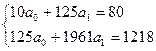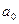= 1,16; 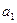= 0,547.

Отсюда = 1,16 + 0,547х.

Подставляя в это уравнение последовательно значения х = 5, 6, 8, 10 и т. д., получаем выравненные (теоретические) значения резуль­тативного показателя (графа 5 таблицы).

Поскольку параметры уравнения регрессии являются оценочными, то для каждого из них рассчитывается средняя ошибка, т. е. .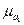

Конкретный расчет ошибок для 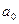и 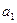по данным нашего при­мера приведен далее.

Б. Для измерения тесноты зависимости между у и х воспользуемся, прежде всего, линейным коэффициентом корреляции (посколь­ку зависимость рассматривалась линейной):

а) по формуле 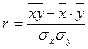находим 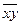= 121,8; 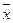= 12,5;

= 8; 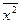= 196,1.

Определяем 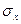и 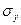, предварительно найдя = 770 и = 77;

,

.

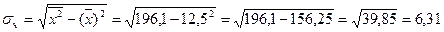Отсюда .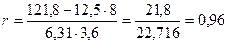

Значение линейного коэффициента корреляции r = 0,96 (т. е. близкое к единице) характеризует не только меру тесноты зави­симости вариации у от вариации х, но и степень близости этой зави­симости к линейной; воспользуемся еще одной формулой линейного коэффициен­та корреляции: ,

т. е. результат тот же.

При расчете коэффициента корреляции, особенно если он ис­числен для небольшого числа наблюдений (n), очень важно оценить его надежность (значимость). Для этого рассчитывается средняя ошибка коэффициента корреляции () по формуле

,

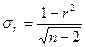где (n-2) — число степеней свободы при линейной зависимости.

А затем находится отношение коэффициента корреляции к его средней ошибке, т.е. 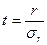, которое сравнивается с табличным значением t-критерия Стьюдента.

В рассматриваемом примере средняя ошибка коэффициента корреляции

,

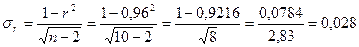а .

По таблице находим, что при числе степеней свободы k = 10-2 = 8 и уровне значимости 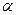= 0,05 табличное (критическое, пороговое) t равно 2,306, т. е. = 2,306.

Поскольку фактическое (расчетное) t больше табличного, т. е. 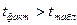, то линейный коэффициент корреляции r = 0,96 считается значимым, а связь между х и у — реальной.

В. Кроме линейного коэффициента корреляции для измерения тесноты зависимости можно воспользоваться теоретическим корре­ляционным отношением:

,

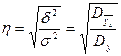где 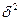и — дисперсии соответственно теоретических и эмпириче­ских значений результативного показателя.

Расчет их показан ниже в таблице.

x	y		y-
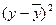
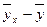
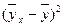
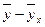
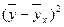
		3,9	-4		-4,1	16,81	0,1	0,01
		4,4	-4		-3,6	12,96	-0,4	0,16
		5,5	-2		-2,5	6,25	0,5	0,25
		5,5	-3		-2,5	6,25	-0,5	0,25
		6,6	-1		-1,4	1,96	0,4	0,16
		6,6			-1,4	1,96	1,4	1,96
		8,8			0,8	0,64	-0,8	0,64
		12,1			4,1	16,81	-2,1	4,41
		12,1			4,1	16,81	-0,1	0,01
		14,3			6,3	39,69	1,7	2,89
			-		--	120,14	—	10,74

Дисперсия выравненных значений результативного показателя, или

факторная дисперсия, ;

общая дисперсия эмпирических значений результативного показателя

;

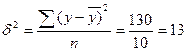теоретическое корреляционное отношение

.

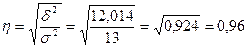Рассчитанные показатели позволяют сделать вывод о том, что связь между вариацией результативного показателя (у) и факторного (х) весьма высокая.

Вместо дисперсии выравненных значений у, т. е. 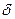², можно вос­пользоваться остаточной дисперсией. В соответствии с правилом сложения дисперсий можно записать, что ,

где 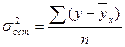, тогда .

В нашем примере расчет остаточной дисперсии () показан в графах 8 и 9 таблицы: = 1,074.

Отсюда .

Остаточная дисперсия, вернее, корень квадратный из нее, т. е. 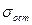, используется для расчета средних ошибок параметров уравнения регрессии.

Так, средняя ошибка параметр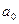а равна ,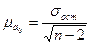

а для 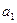равна .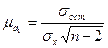

Сопоставляя значение параметра с его средней ошибкой, по значению судят о значимости данного параметра. Если число наблюдений

п > 20, то параметр считается значимым при t >-3.

Если п < 20, то обращаются к специальным таблицам значений t-критерия Стьюдента. И в данном случае пара­метр считается значимым при t факт > .

В рассмотренном примере для уравнения регрессии

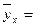1,16 + 0,547х ошибки параметров

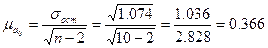, т. е. 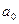= 1,16 ± 0,366,

Дата добавления: 2014-12-24