Для самостоятельной работы 2 страница

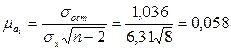, т. е. 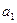= 0,547 ± 0,058.

Чтобы сделать вывод о значимости параметров, находим

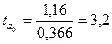и .

Так как п < 20, обращаемся к таблице значений t-критерия. Для 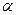=0,05 и А=10-2 = 8 находим = 2,306. Поскольку t > 2,306 и для 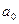, и для 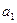, то считаем параметры значи­мыми.

Для измерения тесноты зависимости кроме перечисленных выше существуют и другие показатели. В частности, широко исполь­зуются так называемые ранговые коэффициенты корреляции (или ко­эффициенты корреляции рангов), когда коррелируются не сами зна­чения показателей х и у, а их ранги, т. е. номера их мест, занимаемых в каждом ряду значений по возрастанию или убыванию (обознача­ются ранги буквой R или N. Коэффициент корреляции рангов Спирмэна (р) рассчитывается по формуле

,

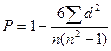где d = Nx - Ny, т. е. разность рангов каждой пары значений х и у;

n — число наблюдений.

Коэффициент корреляции рангов Кендэла () определяется по формуле

.

Порядок расчета этого показателя следующий.

1. Значения х и у ранжируются, т. е. определяются N₁ и N₂.

2. Значения Nx записываются строго в порядке возрастания (или, наоборот, убывания): 1, 2, ….., n.

3. Ранги второго показателя (Ny) располагаются в порядке, со­ответствующем значению х в исходных данных.

4. Для каждого значения Ny подсчитываем число следующих за ним рангов более высокого порядка. Общая сумма таких случаев «правильного следования» последовательно для всех рангов учитывается как баллы со знаком «—» и обозначается буквой Р.

5. Аналогично для каждого значения Ny последовательно под­считывается число следующих за ним рангов, меньших по значению. Общая сумма таких случаев (инверсий) учитыва­ется как баллы со знаком «—» и обозначается символом Q.

6. Определяется общая сумма баллов, которая обозначается символом S,т. е. S = Р + Q.

7. Полученная сумма (S) сопоставляется с максимальной, которая равна 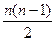в случае, если в обоих рядах ранги следуют строго последовательно от 1 до n.

Рассмотрим расчет ранговых коэффициентов корреляции Спирмэна и Кендэла на конкретном примере.

Задача 6.2

По данным 10 предприятий (графы 1 и 2 приводимой ниже таблицы) с помощью коэффициентов корреляции рангов Спирмэна (р) и Кендэла () измерить тесноту зависимости между объемом выпус­ка продукции (у), млн. руб., и стоимостью основных производствен­ных фондов (х), млн. руб.

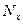
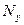
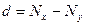
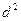
х	У					Подсчет	баллов
«+»	«—»
1,5 1,8 2,0 2,2 2,3 2,6 3,0 3,1 3,5 3,8	3,9 4,4 3,8 3,5 4,8 4,3 7,0 6,5 6,1 8,2			-2 -3 -1 -2		-	-
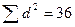
						P=35	Q=-10

Решение.

А. Для расчета коэффициента корреляции рангов Спирмэна (р)

вначале ранжируем значения признаков в каждом ряду, т.е. каждому значению х и у в порядке их возрастания присваиваем порядковый номер (ранг) 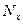и 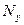(графы 3 и 4 таблицы), затем находим разности рангов (d), возводим их в квадрат (графа 6 таблицы) и суммируем.

Полученную сумму 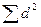подставляем в формулу

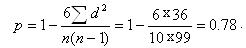
Судя по значению полученного коэффициента, связь между х и у довольно большая.

Б. Для расчета коэффициента корреляции рангов Кендэла

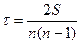определяем S в соответствии с описанным выше порядком как сумму положительных (Р) и отрицательных (Q) баллов.

Вспомогательные расчеты этих баллов показаны в графах 7 и 8 таблицы. Так как значения рангов х идут строго в возрастающем по­рядке, то следим лишь за поведением рангов у. Например, после первой пары значений рангов, где Nу = 3, в семи случаях идут значе­ния Ny > 3, а в двух случаях значения Ny < 3 (Ny =2, 1); после второй пары, где N= 5, наблюдается пять случаев рангов у выше рассматриваемого, а три (Ny = 2, 1,4) ниже и т. д.

По результатам подсчетов находим общую сумму баллов

S = Р + Q = 35 - 10 = 25.

Подставляя ее в формулу коэффициента корреляции рангов Кендэла (), определяем

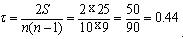
Коэффициент Кендэла всегда меньше по значению, чем коэффициент Спирмэна .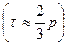

Интерпретация значений ранговых коэффициентов корреляции аналогична любым другим, т. е. чем ближе значение р или к 1, тем теснее зависимость, а близость к нулю означает отсутствие связи или весьма малую зависимость.

Рассмотрим еще пример, где ранги повторяются.

Задача 6.3

По данным 10 хозяйств с помощью коэффициентов корреляции рангов Спирмэиа и Кендэла измерить тесноту зависимости между урожайностью картофеля и количеством внесенных минеральных удобрений.

Удобрения, кг/га, х	Картофель, ц/гa, у	Nж	NУ	d =	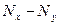d^2	Подсчет баллов
					«+»	«—»
		3,5 3,5 8,5 8,5	1,5 1,5	-0,5 0,5 -0,5 0,5 -1 0,5 -1,5 1,0	0,25 0,25 0,25 0,25 1,00 1,00 0,25 2,25 1,00	-	-
					6,5	P=39	Q = -2

В данном примере отдельные значения х и у повторяются. При ранжировании повторяющихся значений им присваивается ранг, рассчитанный как средняя арифметическая из суммы мест, которые они занимают по возрастанию.

Расчет рангов показан в графах 3 и 4.

Для случая повторяющихся рангов есть особые скорректирован­ные формулы и для коэффициента Спирмэна, и для коэффициента Кендэла.

Однако на практике часто пользуются приведенной выше фор­мулой Спирмэна и для случая повторяющихся рангов, поскольку ошибку она дает весьма малую.

В нашем примере .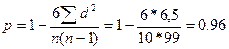

Формула коэффициента Кендэла для повторяющихся рангов имеет вид

,

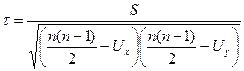где S = Р + Q, как и раньше, a Ux и Uy — показатели, корректирую­щие максимальную сумму баллов и определяемые по формуле ,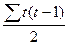

где (t- число повторяющихся рангов в соответствующем ряду х и у

В нашем примере .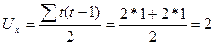

а .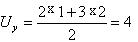

Баллы Q и Р определяются так же, как и в задаче 8.2, с тем лишь добавлением, что в случае одинакового (повторяющегося) значения ранга, следующего за рассматриваемыми в любом из рядов (х и у), последний при подсчете баллов не учитывается ни со знаком «+», ни со знаком «—».

Расчет Р и Q показан в графах 7 и 8 таблицы, по результатам подсчетов

S = Р + Q = 38 - 1 = 37.

Отсюда коэффициент корреляции рангов Кендэла

.

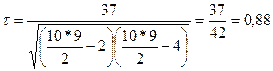По величине коэффициента ( = 0,88) можно сделать вывод о весьма большой тесноте зависимости между х и у.

ИЗУЧЕНИЕ ВЗАИМОСВЯЗИ НА ОСНОВЕ АНАЛИЗА ТАБЛИЦ ВЗАИМОСОПРЯЖЕННОСТИ

Особое место в изучении взаимосвязи занимает исследование особенностей распределения единиц совокупности по двум призна­кам. По характеру распределения можно судить, случайно оно или нет, т.е. есть ли зависимость между признаками, положенными в ос­нову группировки, или нет.

Покажем это на примере.

Задача 6.4

По одному из факультетов имеются следующие данные о рас­пределении 600 студентов-вечерников по двум признакам: характеру работы и результатам сдачи экзаменов по специальным предметам:

Характер работы	Сдавшие сессию без неудовлетворительных оценок	Получившие неудовлетворительные оценки	Всего студентов
Работающие по про­филю факультета	а 270(224)	b 50(96)
Работающие не по профилю факультета	с 150(196)	d 130(84)
Всего студентов

1. Определить, случайно или неслучайно распределение в таб­лице, т. е. сделать вывод о наличии или отсутствии зависимо­сти успеваемости студентов-вечерников от соответствия про­филя работы.

2. Измерить тесноту этой зависимости, если она есть.

Решение.

А. Для ответа на первый вопрос воспользуемся критерием Пир­сона ():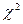

,

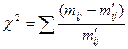где 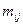— эмпирические частоты таблицы; 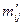— теоретические частоты.

Последние рассчитываются по каждой строке (или столбцу) пропорционально общим итогам, исходя из гипотезы о случайности распределения. В нашем примере теоретические частоты показаны в
скобках (например, 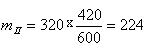и т. д.).

.

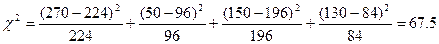Определяем число степеней свободы

k = (k1 —1)(к2 - 1) = (2 - 1) (2 - 1) = 1,

где к1 и к2 — число строк и столбцов.

Чтобы сделать вывод о случайности или неслучайности распределения, определяем табличное (пороговое) зна­чение 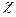2, допустимое при случайных расхождениях между эмпириче­скими (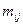) и теоретическими (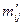) частотами.

Для уровня значимости α = 0,05 и числа степеней свободы к = 1 значение х₂табл = 3,84, а х₂факт = 67,5. Так как х₂факт > х₂та6л, делаем вывод, что распределение неслучайно и скорее связано с зависимо­стью между признаками, положенными в основу группировки, т. е. можно говорить о зависимости между характером работы студен­тов-вечерников и результатами сдачи ими экзаменов по специаль­ным предметам.

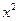помогает выявить наличие или отсутствие зависимости меж­ду признаками, положенными в основу группировки в таблицах со­пряженности, но не измеряет тесноту этой связи.

Б. Для измерения тесноты зависимости между указанными при­знаками используются следующие показатели:

1. Коэффициент ассоциации

Касс= .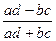

2. Коэффициент контингенции

.

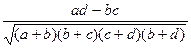В обеих формулах а, b, с, d — значения частот в четырехклеточной таблице

a b

c d.

3. Коэффициент взаимной сопряженности Пирсона

C= 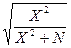, или С= 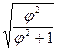, где .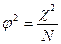

Показатель φ² можно рассчитать и самостоятельно:

где 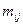— частоты в клетках таблицы, а M_i и M_j — итоговые частоты по строкам и столбцам.

Коэффициент взаимной сопряженности Чупрова

,

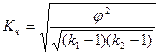где k₁ и k₂ — число строк и столбцов в таблице.

Первые два показателя (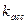 и 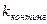) могут использоваться только для четырехклеточных таблиц, а коэффициенты сопряженности Пирсона и Чупрова — для таблиц любой размерности.

В нашем примере (задача 6.4) для четырехклеточной таблицы (или таблицы «четырех полей»):

а) ;

б) ;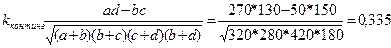

в) 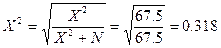, или

если 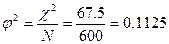, то ,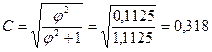

г) .

Все рассчитанные выше показатели, кроме коэффициента ассо­циации, свидетельствуют о том, что зависимость между характером работы у студентов-вечерников и результатами сдачи экзаменов по специальным предметам ниже средней.

Задача 6.5

Предположим, имеется следующее распределение 100 опытных участков (под овощной культурой) по двум признакам: степени полива (х) и уровню урожайности (у).

Урожайность   полив	Высокая	Средняя	Низкая	Итого
Обильный	40 (33)	10 (12,1)	5 (9,9)
Средний	20 (18)	7 (6,6)	3 (5,4)
Слабый	- (9)	5 (3,3)	10 (2,7)
Итого

Определить, случайно ли данное распределение, т. е. есть ли зависимость между х и у.

Измерить тесноту зависимости между степенью полива и уровнем урожайности.

Решение.

Для определения зависимости между х и у:

а) выдвигаем гипотезу о случайности распределения и рассчитываем теоретические (гипотетические) частоты в каждой строке пропорционально итоговым данным. (Например, если в итоговой строке суммы столбцов составляют 0,6, 0,22 и 0,18 от 100, то в каждой строке ее итога сохраняется такое же соотношение.) Теоретические частоты (m_ij) показаны в таб­лице в скобках;

б) рассчитываем χ² (фактическое):

По таблице находим χ² табличное при уровне значимости а = 0,05 и числе степеней свободы k=(3 — 1)(3—1) = 4 = 9,49, так как χ²_факт > χ²_табл (35,2 > 9,49) при а = 0,05 и к = 4, то гипотеза о случайности распределения опровергается, т. е. распределение в таблице неслучайно.

Следовательно, есть основа­ния предполагать наличие зависимости между x и y.

2. Для измерения тесноты зависимости используем

а) коэффициент взаимной сопряженности Пирсона

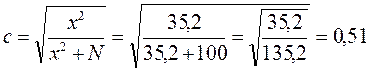
или, если рассчитать

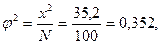то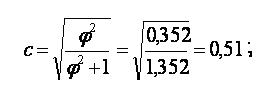

б) коэффициент Чупрова

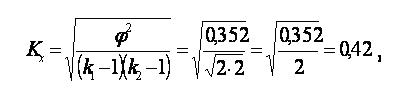
(К_ч всегда по значению несколько меньше С.)

Полученные значения коэффициентов (0,51 и 0,42) позволяют сделать вывод о том, что зависимость между х и у средняя.

Примечание: φ² можно было рассчитать независимо от χ² т. е. по формуле

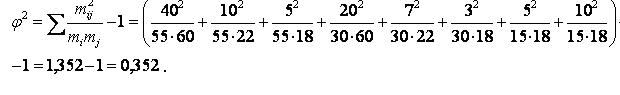
Контрольные вопросы

1. В чем сущность корреляционной связи (зависимости) между показателями?

2. Как определяются параметры уравнения регрессии при ли­нейной зависимости (на основе способа наименьших квад­ратов)?

3. Как определяются параметры уравнения регрессии криволи­нейной зависимости?

4. Как определяется ошибка параметров уравнения регрессии?

5. Какие вы знаете показатели измерения тесноты зависимос­ти?

6. Как измеряется теснота зависимости с помощью корреляци­онного отношения?

7. Какие формы линейного коэффициента корреляции вы знаете?

8. Как оценивается значимость коэффициента корреляции, рассчитанного по выборочным данным?

9. Каково содержание корреляционной таблицы и какова ее роль в изучении взаимосвязи между двумя показателями?

10. Определите понятие множественной корреляции.

11. Что такое совокупный и частный коэффициенты корреля­ции?

12. Что представляют собой коэффициенты корреляции рангов Спирмэна и Кендэла?

13. С помощью каких показателей изучается и измеряется кор­реляционная зависимость между качественными показателя­ми на основе таблиц взаимосопряженности?

14. Что такое коэффициент конкордации? Как он рассчитыва­ется?

Дата добавления: 2014-12-24