Таможенный контроль

Конуси

При обертанні будь-якої прямої L, що перетинає вісь обертання, утворюється прямий круговий конус (рис.16.11). Точка перетину прямої, яка обертається, з віссю обертання залишається нерухомою, її називають вершиною конуса.

Рис.16.11. Прямий круговий конус

Рівняння будемо виводити в прямокутній системі координат (вісь Oz є віссю обертання, початок системи координат збігається з вершиною конуса). Вісь Ох розташуємо так, щоб пряма L перебувала в координатній площині Oxz і описувалася рівнянням . У цій системі координат рівняння поверхні обертання отримується з рівняння прямої заміною х на . У результаті такої заміни одержуємо . Піднесемо обидві частини рівняння в квадрат: 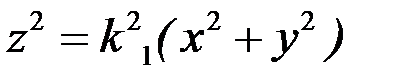. Розділимо його на і отримаємо канонічне рівняння прямого кругового конуса:

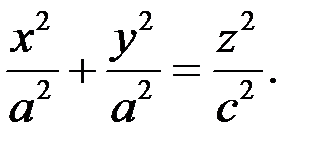
Перетворення стиснення прямого кругового конуса до координатної площини Оxz з коефіцієнтом k дає елліптичний конус. Його рівняння має вигляд:

або, після введення відповідних замін:

(16.9)

Рівняння (16.9) називають канонічним рівнянням еліптичного конуса. Еліптичний конус при а = b збігається з прямим круговим конусом, і обидва вони є поверхнями другого порядку.

16.8. Циліндричні поверхні

При обертанні прямої навколо осі обертання, що паралельна цій прямій, утворюється поверхня, яку називають круговим циліндром (рис.16.12). Ця поверхня є окремим випадком циліндричної поверхні, що отримується при русі прямої в просторі вздовж деякої кривої і яка паралельна деякому напрямку (рис.16.13). Якщо на рухомій прямий фіксувати точку, то вона опише криву, яку називають напрямною циліндричної поверхні. Циліндрична поверхня є множиною точок на прямих, що паралельні фіксованій прямій. Ці паралельні прямі називають твірними циліндричної поверхні.

Рис. 16.12. Круговий циліндр Рис. 16.13. Циліндрична поверхня

Виберемо прямокутну систему координат так, щоб твірні циліндричної поверхні були паралельні осі Оz. В якості напрямної виберемо криву, яка є перетином циліндричної поверхні з координатною площиною хОу

(рис. 16.14).

Рис.16.14. Циліндрична поверхня

Напрямна в площині хОу описується деяким рівнянням двох змінних . Точка М(х; у; z) лежить на циліндричній поверхні тоді і тільки тоді, коли її абсциса і ордината (фактично координати точки N(x; y; 0) на площині хОу) підкоряються рівнянню напрямної. Тому в обраній системі координат циліндрична поверхня описується рівнянням - рівнянням своєї напрямної, яке трактується як рівняння трьох змінних х, у і z. Вірне і зворотне твердження: якщо в деякій прямокутній системі координат в просторі поверхня описується рівнянням, що не містить одної зі змінних, то ця поверхня є циліндричною. Отже, критерієм для циліндричної поверхні є відсутність в її рівнянні у підходящий системі координат однієї зі змінних.

Циліндр другого порядку - це циліндрична поверхня, напрямна якої в площині, що перпендикулярна твірній, є кривою другого порядку. У вибраній вище прямокутній системі координат циліндр другого порядку описується рівнянням другого степеня

,

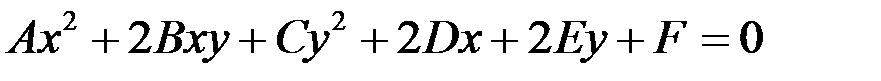де .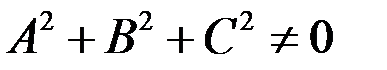

Це рівняння можна спростити вибором системи координат. Фактично мова йде про приведення до канонічного вигляду рівнянь другого порядку від двох змінних. Канонічні рівняння кривих другого порядку приводять до трьох видів циліндрів другого порядку:

- еліптичному (рис. 16.15, а) з канонічним рівнянням ;

- гіперболічному (рис. 16.15,б) з канонічним рівнянням ;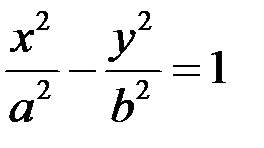

- параболическому з канонічним рівнянням (рис. 16.15, в).

Рис. 16.15. Циліндричні поверхні.

16.9. Метод перерізів

Для з'ясування форми поверхні в просторі по її рівнянню

(16.10)

часто використовують так званий метод перерізів. Метод полягає в аналізі перетинів поверхні з площинами, паралельними координатним площинам, наприклад з площинами виду z = с, де параметр с пробігає всі дійсні значення. Для кожного значення с система рівнянь

(16.11)

задає відповідний перетин. Точки М (х; у; z) належать перетину, якщо виконані умови: а) z = с; б) координати x та у її проекції на координатну площину хОу, тобто координати точки N (x; у; 0), задовольняють рівнянню

(16.12)

Аналізуючи форму кривих перетинів можна представити форму поверхні.

◄Приклад 16.1. Дослідити рівняння методом перетинів.

Розв’язання.

Перетин цієї поверхні з площиною z = c описується рівнянням

При c <0 перетин порожній, при с = 0 він збігається з початком системи координат Охуz, а при с > 0 представляє собою еліпс

.

Осі цього еліпса із зростанням параметра с збільшуються, і можна уявити форму поверхні (рис. 16, а).

Перетини цієї ж поверхні як із площинами х = с (рис. 16, б), так і з площинами у = с (рис. 16, в) є параболами

відповідно. Параболи в кожному з цих сімейств перерізів мають рівні параметри, які залежать від значення с.

Дослідження методом перетинів дозволило визначити цю поверхню як еліптичний параболоїд. Метод дозволяє дати ще одну геометричну побудову еліптичного параболоїда. Розглянемо параболу , що знаходиться в площині у = 0, і аналогічну параболу в площині х = 0 (рис. 16.17, а). Нехай друга парабола переміщається в просторі так, що:

- вершина параболи 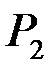весь час знаходиться на параболі ;

- вісь параболи 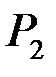паралельна осі параболи ;

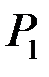- площина параболи перпендикулярна площині параболи .

Тоді в результаті такого переміщення та утворюється еліптичний параболоїд. При цьому ролі парабол і можна поміняти,, тобто переміщати параболу , використовуючи параболу як направляючу.

Рівняння відрізняється від рівняння еліптичного параболоїда лише знаком одного доданка і теж задає поверхню другого порядку. Її називають гіперболічним параболоїдом, а саме рівняння - канонічним рівнянням гіперболічного параболоїда.

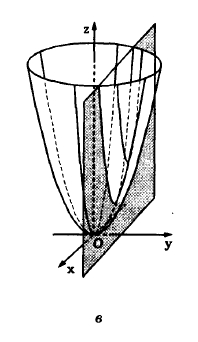
Рис. 16.16. Побудова еліптичного параболоїда

Рис. 16.17. Еліптичний та гіперболічний параболоїди

Досліджуємо вид гіперболічного параболоїда методом перерізів. Його перетин з площинами у = с при будь-якому значенні с є параболами:

Перетини з площинами х = с теж при всіх значеннях с є параболами:

Позначимо через параболу, що знаходиться в перерізі у = 0, а через - аналогічну параболу в перерізі х = 0. Переміщуючи, як і вище, параболу по параболі (рис. 16.17.6), отримуємо сідлоподібну поверхню гіперболічного параболоїда.

Перетин гіперболічного параболоїда з площинами z = c при є гіперболами , а при с = 0 парою пересічних прямих:

.

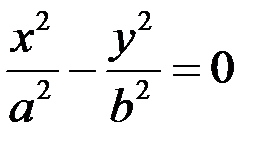Вибір назви поверхні пояснюється характером перетинів: горизонтальні перетини гіперболічного параболоїда - це гіперболи, а два інших сімейства розглянутих перетинів - параболи.

УЧЕБНОЕ ПОСОБИЕ

Дата добавления: 2014-12-25