
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Поверхности отклика
|
|
|
|
Планы эксперимента для исследования
1. Под понятием поверхность отклика подразумевается геометрическая интерпретация точной регрессионной зависимости, как функции многих переменных – факторов эксперимента:
 (2.4.1)
(2.4.1)
Целью эксперимента в данной ситуации является не столько установление собственно формы зависимости (2.4.1), а то, чтобы с минимальными временными и иными затратами по возможности определить положение экстремальной точки этой поверхности в реализуемом диапазоне варьирования факторов. Если отклик интерпретируется как выход некоего продукта, то очевидно целью является точка максимума. Если же отклик представляет собой издержки, то, соответственно, целью будет точка минимума. Задачи подобного типа известны в численных методах оптимизации, когда требуется найти экстремум некоторой детерминированной функции многих переменных, имеющей сложный вид. Общей проблемой здесь является то, что для гарантированной результативности какой-либо из простейших схем последовательного поиска необходимым условием является гладкость и унимодальность (существование не более чем одного экстремума) в исследуемой области пространства. Из сказанного ясно, что реальная практическая польза от экспериментов данного типа определяется тем, насколько соответствуют действительности эти априорные гипотезы.
Простейший вариант схемы эксперимента для поиска экстремума включает 2 этапа. Сначала по минимальному числу экспериментальных точек N =2k, где k - число факторов, строится линейная аппроксимация регрессии. На полученной плоскости определяется направление градиентной линии, точки (ядро плана) смещаются в нужном направлении (по градиенту в сторону максимума и в противоположном – в сторону минимума), и эксперимент повторяется при новых значениях уровней факторов. Критерием остановки такой итерационной процедуры служит либо инверсия градиента на очередном шаге (такая ситуация характерна при большом шаге смещения), либо стабилизация направления градиента значений отклика. Вторая ситуация характерна для малой величины шага смещения по факторному пространству. В геометрической интерпретации это означает, что аппроксимирующая плоскость заняла положение, близкое к горизонтальному (достигла почти стационарной области). В рассмотренной процедуре, вообще говоря, существует возможность выхода за границы реализуемого диапазона варьирования факторов без попадания в почти стационарную область. Это означает, что либо экстремума не существует, либо траектория движения прошла мимо области экстремума.
|
|
|
Вторая фаза активного эксперимента заключается в более детальном обследовании области предполагаемого экстремума. Для этого к ядру плана добавляется еще некоторое количество точек (рассмотрим схему N =2k+2k+1). Для оценки случайной ошибки эксперимент по рандомизованной процедуре дублируется во всех или нескольких точках нового плана. Затем по средним значениям методом наименьших квадратов регрессия отклика аппроксимируется поверхностью 2-го порядка. Если полученная аппроксимация имеет удовлетворительную адекватность, то в качестве искомого экстремума отклика принимается точка экстремума аппроксимирующей поверхности 2-го порядка. При этом следует сделать оговорку, что достоинства поверхностей 2-го порядка исчерпываются их полной классификацией (4 типа), минимальным объемом вычислений по методу наименьших квадратов и, в целом, тем, что они представляют собой простейшую степенную функцию, имеющую экстремум. О «физическом» смысле такой аппроксимации в общем случае сказать ничего нельзя.
|
|
|
2. Детали алгоритма и, в частности, ортогональные преобразования и вычислительную процедуру метода наименьших квадратов рассмотрим на модельном примере. В качестве модельного двухфакторного объекта возьмем биквадратный параболоид
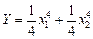 (2.4.2)
(2.4.2)
в области 
Минимум (2.4.2) очевидно находится в точке (0,0), но для наглядного представления о процедуре последовательного линейного градиентного спуска условимся, что наш виртуальный эксперимент будет заключаться в вычислении функции (2.4.2) в выбранных экспериментальных точках плоскости x 1 ox 2. При этом «притворимся», что сама поверхность, задаваемая (2.4.2), нам не видна. В принципе можно добиться большого сходства с натурным экспериментом, добавив к (2.4.2) случайное слагаемое Z с нулевым средним. Тогда при повторных вычислениях в одной точке функция будет изме-няться, и вместо поверхности будем наблюдать поле рассеяния в 3-мерном пространстве, регрессией которого будет поверхность (2.4.2).
Пусть на первом шаге факторы варьируются в соответствии с табл. 2.4.1.
Таблица 2.4.1. План-матрица эксперимента
на первом шаге
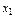
| 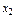
| 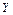
|
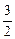
| 
| 
|
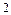
| 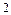
|  .00 .00
|
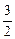
| 
| 
|
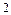
| 
| 
|
Линейную аппроксимацию регрессии ищем в виде
 (2.4.3)
(2.4.3)
а неизвестные коэффициенты из условия минимализма суммы квадратов отклонений:
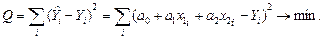 (2.4.4)
(2.4.4)
Дифференцируя сумму квадратов по  и приравнивая частные производные к нулю, получаем систему нормальных уравнений:
и приравнивая частные производные к нулю, получаем систему нормальных уравнений:
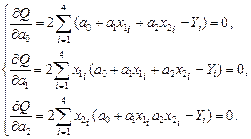 (2.4.5)
(2.4.5)
Чтобы избавить себя от необходимости на каждой итерации решать систему уравнений вида (2.4.5), перейдем к безразмерным переменным (кодированным факторам), что дополнительно позволит унифицировать вычислительный аппарат безотносительно фактического диапазона варьирования факторов:
 (2.4.6)
(2.4.6)
План-матрица в кодированных уровнях приведена в табл. 2.4.2.
Таблица 2.4.2. План-матрица эксперимента
в кодированных факторах
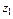
| 
| 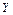
|

| 
| 
|

| 
| 
|
| 
| 
|
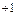
| 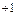
| 
|
Суммы столбцов 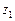 и
и 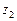 , а также их скалярное произведение теперь равны нулю, и система уравнений (2.4.5) автоматически приобретает диагональный вид:
, а также их скалярное произведение теперь равны нулю, и система уравнений (2.4.5) автоматически приобретает диагональный вид:
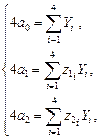 (2.4.7)
(2.4.7)
откуда получаем систему разрешающих соотношений для коэффициентов линейной регрессии:
 (2.4.8)
(2.4.8)
Подставляя в (2.4.8) данные табл. 2.4.2, получаем уравнение линейной регрессии на первой итерации:
|
|
|
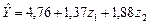 . (2.4.9)
. (2.4.9)
Линии уровня плоскости  , очевидно представляют собой семейство параллельных прямых. Координаты направляющего вектора линии уровня в пространстве
, очевидно представляют собой семейство параллельных прямых. Координаты направляющего вектора линии уровня в пространстве 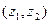 (с точностью до линейного преобразования) находим, разрешив (2.4.9) относительно
(с точностью до линейного преобразования) находим, разрешив (2.4.9) относительно  Направляющий вектор градиент-ной линии (перпендикуляра к линиям уровня) находим из условия
Направляющий вектор градиент-ной линии (перпендикуляра к линиям уровня) находим из условия 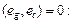

Значения линейной аппроксимации (2.4.9) в точках плана (2.4.2), линии уровня и градиентная линия, проходящие через центр плана, показаны на рис. 2.4.1.

Рис. 2.4.1. Значения линейной аппроксимации
и направление градиента на первой итерации
Из схемы на рис. 2.4.1 очевидно, что антиградиент направлен вниз и влево (противоположное направление является направлением градиентного восхождения). Примем “осторожную стратегию” движения, а именно, за новый центр ядра плана примем точку пересечения антиградиента с границей исходного ядра (рис. 2.4.1). Новые уровни z 1 и z 2 возьмем симметрично (влево/вправо, вверх/вниз) относительно нового центра: z 1={-1,46;0}, z 2 ={-2;0}. Для «реализации» эксперимента необходимо совершить пересчет новых уровней вещественных факторов x 1 и x 2. Обращая преобразования (2.4.6), получим
 , (2.4.10)
, (2.4.10)
где верхний индекс соответствует номеру итерации. Подставляя в (2.4.10) данные табл. 2.4.1, находим:



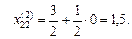
Подставляя найденные значения в (2.4.2) (реализуем новый эксперимент), и учитывая универсальность плана в кодированных переменных, получаем план-матрицу табл. 2.4.3.
Таблица 2.4.3. План-матрица эксперимента
на второй итерации
| z1 | z2 | y |
| -1 | -1 | 0,95 |
| -1 | +1 | 2,2 |
| +1 | -1 | 2,36 |
| +1 | +1 | 3,61 |
По данным табл. 2.4.3 получаем уравнение линейной регрессии на второй итерации:

 (2.4.11)
(2.4.11)
Аналогично рис.2.4.1 строим новую схему расположения линии уровня и градиентной линии (рис. 2.4.2):
ес =(1;-1,13), 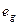 =(1;0,89).
=(1;0,89).
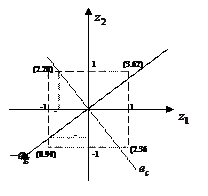
Рис.2.4.2. Значения линейной аппроксимации
и направление градиента на второй итерации
Сравнивая рис. 2.4.2 с рис.2.4.1, замечаем, что градиентная линия немного развернулась по часовой стрелке. Новые значения уровней z 1, z 2 составят z 1={–2; 0}, z 2 ={–1,88; 0}. Соответствующие им уровни x 1, x 2 находим, обновляя значения в (2.4.10):
|
|
|

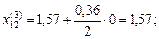


Обновленная план-матрица эксперимента приведена в табл.2.4.4.
Таблица 2.4.4. План-матрица эксперимента
на третьей итерации
| z1 | z2 | y |
| -1 | -1 | 0,54 |
| -1 | +1 | 0,79 |
| +1 | -1 | 1,52 |
| +1 | +1 | 1,77 |
Уравнение линейной регрессии теперь примет вид:
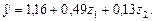
 (2.4.12)
(2.4.12)
Схема плоскости (2.4.12) показана на рис.2.4.3.

Рис.2.4.3. Значения линейной аппроксимации
и направление градиента на третьей итерации
Значения уровней z и x теперь составят:
z 1={–2; 0}; z 2 ={–0,54; 0}; x 1={1,03; 1,39}; x 2 ={0,28; 0,53}.
Новая план-матрица приведена в табл. 2.4.5.
Таблица 2.4.5. План-матрица эксперимента
на четвертой итерации
| z1 | z2 | y |
| -1 | -1 | 0,28 |
| -1 | +1 | 0,3 |
| +1 | -1 | 0,93 |
| +1 | +1 | 0,95 |
3. Как показывают результаты последовательного спуска, «осторожная» стратегия приближает к цели, хотя и не так быстро, как хотелось бы. В принципе, шаги в направлении антиградиента могли быть и больше. Однако в реальности вид исследуемой поверхности далеко не всегда так очевиден, как в нашем модельном примере. При большем числе факторов ситуация еще более усложняется, и потеря направления спуска на очередной итерации может привести к необходимости начинать эксперимент практически заново.
Предположим, что на очередной итерации алгоритм последовательного линейного градиентного спуска позволил достичь почти стационарной области, и ядро плана составили точки с координатами x 1={–0,2; 0,3}, x 2 ={–0,3; 0,1}.
Далее переходим ко второй фазе активного эксперимента – аппроксимации поверхности отклика полиномом второго порядка. Уравнение регрессии теперь будем иметь в виде

 (2.4.13)
(2.4.13)
Уравнение (2.4.13) содержит уже 6 неизвестных коэффициентов, и соответственно система нормальных уравнений метода наименьших квадратов содержит также 6 линейных уравнений.
Для приведения этой системы уравнений к диагональному виду используется ортогональное преобразование (ортогональный центрально-композиционный план второго порядка). рассмотрим данное преобразование в общем виде, т.е. для произвольного числа факторов k. К ядру плана, содержащему 2k точек (вершин гиперкуба с координатами –1;+1), в пространстве кодированных переменных добавляется 2 k точек (по 2 для каждой оси), расположенных симметрично относительно центра плана на расстоянии а. Эти точки принято называть «звездными», и ортогонализация плана достигается за счет выбора величины  – «плеча звездных точек». Здесь сразу следует отметить, что радиус гиперсферы, проведенной из центра плана через звездные точки, возрастает с увеличением k, т.е. с увеличением числа факторов звездные точки раздвигаются от центра, увеличивая таким образом эффективный объем обследуемой области факторного пространства.
– «плеча звездных точек». Здесь сразу следует отметить, что радиус гиперсферы, проведенной из центра плана через звездные точки, возрастает с увеличением k, т.е. с увеличением числа факторов звездные точки раздвигаются от центра, увеличивая таким образом эффективный объем обследуемой области факторного пространства.
Обозначим через φ средний скалярный квадрат (на одну точку плана) столбца уровней фактора. Учитывая, что из N =2 k +2 k +1 элементов столбца (точек плана) 2k-1 равны –1, столько же имеют значение +1, по одному значению – α и + α, а остальные равны 0, получим
 (2.4.14)
(2.4.14)
таким образом, столбец  будет иметь нулевую сумму. Приравнивая нулю скалярное произведение двух столбцов (
будет иметь нулевую сумму. Приравнивая нулю скалярное произведение двух столбцов ( )=0, получаем уравнение относительно α:
)=0, получаем уравнение относительно α:
 . (2.4.15)
. (2.4.15)
Исключая из (2.4.15) φ, используя (2.4.14), после элементарных преобразований получаем
 (2.4.16)
(2.4.16)
При увеличении k от 2 до 4, α согласно (2.4.16) возрастает от 1 до 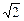 .
.
Разрешающие соотношения метода наименьших квадратов в ортогональных переменных будут иметь вид:



 (2.4.17)
(2.4.17)
Соотношение (2.4.17) можно облечь в простую естественную формулировку: коэффициент квадратичной регрессии определяется в виде дроби:
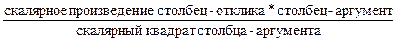 .
.
При переходе от переменных 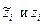 требуется пересчитать только свободный член:
требуется пересчитать только свободный член:
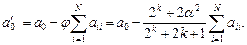 (2.4.18)
(2.4.18)
Возвращаясь к модельному примеру, получаем план-матрицу ЦКП в виде табл.2.4.6.
Параметры плана 22 составят: α =1, φ= 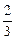 .
.
Таблица 2.4.6. План-матрица ЦКП второго порядка 22
| i | z1 | x1 | z2 | x2 | z1 z2 | 
| 
| y 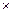 10-3 10-3
|
| -1 | -0,2 | -1 | -0,3 | 
| 
| 2,43 | ||
| -1 | -0,2 | 0,1 | -1 | 
| 
| 0,43 | ||
| 0,3 | -1 | -0,3 | -1 | 
| 
| 4,05 | ||
| 0,3 | 0,1 | 
| 
| 2,05 | ||||
| -α(-1) | -0,2 | -0,1 | 
| 
| 0,43 | |||
| α(1) | 0,3 | -0,1 | 
| 
| 2,05 | |||
| 0,05 | -α(-1) | -0,3 | 
| 
| 2,03 | |||
| 0,05 | α(1) | 0,1 | 
| 
| 0,03 | |||
| 0,05 | -0,1 | 
| - 
| 0,03 |
Подставляя данные табл. 2.4.6 в (2.4.17), находим коэффициенты уравнения квадратичной регрессии, умноженные на 1000:
 (2.4.19)
(2.4.19)
или, возвращаясь от переменных  к
к  ,
,
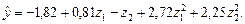 (2.4.20)
(2.4.20)
Минимум квадратичной формы (2.4.20) достигается в точке z 1= –0,149; z 2 =0,222, что соответствует уровням вещественных переменных x 1=0,013; x 2 = –0,056.
Таким образом, как показывает приведенный демонстрационный пример, аппроксимация поверхности отклика полиномом 2-го порядка имеет сугубо ориентировочный характер. Поэтому при интерпретации результатов анализа такой модели, построенной по усеченным выборочным данным, следует соблюдать осторожность. По крайней мере, эти результаты не стоит абсолютизировать.
Глава 3. Системный анализ контрольных
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 5033; Нарушение авторских прав?; Мы поможем в написании вашей работы!