Выборочные оценки параметров распределения

1. При практическом применении статистических методов для анализа качества продукции, стабильности и точности технологических и измерительных процессов чаще всего приходится иметь дело со статистическим материалом ограниченного объема - 10÷100 измерений, либо сериями 5÷25 проб - малых выборок по 3÷7 измерений. Такого ограниченного материала недостаточно, чтобы найти заранее неизвестный закон распределения, хотя можно определить его важнейшие числовые характеристики: среднее и дисперсию либо параметры априорно известного закона распределения. Оценкой неизвестного параметра θ называется СВ, представляющая собой функцию выборочных значений 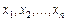: , вид которой определяется, исходя из «физического смысла» параметра θ и информации о законе распределения СВ X.

В качестве оценки математического ожидания чаще всего используется выборочное среднее: .Числовые характеристики 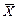равны: , .

Несмещенная выборочная оценка дисперсии, как известно, имеет вид

.

Однако выборочное СКО не является несмещенной оценкой параметра 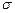. В этом легко убедиться, рассмотрев дисперсию s: .

Поскольку , приходим к очевидному выводу, что .

Это отрицательное смещение оценки s при выборках небольшого объема может приводить к заниженной оценке средней ширины зоны рассеивания процесса, приводя тем самым к завышенной оценке числовых индексов (Ср, Срк и т.д.).

2. Для установления ПР величин 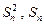и определения несмещенной оценки рассмотрим нормированную сумму квадратов отклонений: . Используя тождественное преобразование, представим в следующем виде:

Внося и 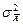под знак квадрата, убеждаемся, что каждое из слагаемых представляет собой СВ - квадрат стандартной нормальной СВ. Перепишем (1.4.1) в виде . Поскольку 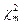аддитивна по степеням свободы (), приходим к выводу, что

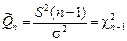. (1.4.2)

Величина 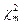была рассмотрена в п.1.2. Используя формулу линейного преобразования (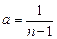), найдем ПР :

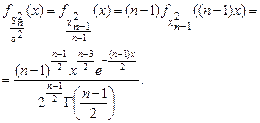(1.4.3)

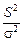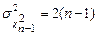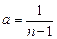Среднее равно 1. Дисперсию найдем, используя соотношение и формулу для дисперсии нормированной СВ . Полагая , получаем

. (1.4.4)

Числовые характеристики выборочной дисперсии соответственно составят:

, (1.4.5)

Для нормированного выборочного СКО 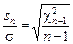ПР найдем, используя преобразование :

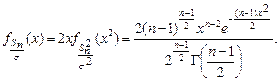(1.4.6)

Рассмотрим структуру последовательности . Для легко вычисляются и составляют: , 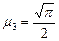. Рассмотрим случай n > 3:

Первое слагаемое равно 0. Второе слагаемое подстановкой , используя рекуррентное свойство , преобразуем к виду

(1.4.7)

Заменяя в рекуррентном соотношении (1.4.7) () и используя рекуррентное свойство Гамма-функции, по индукции получаем формулу общего члена последовательности :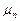

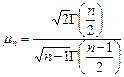, . (1.4.8)

Таким образом, несмещенную точечную выборочную оценку СКО получим, устранив отрицательное смещение М[S] тем же приемом, что и для s ²:

(1.4.9)

В табл. 1.4.1 приведена величина относительной ошибки в зависимости от объема выборки.

Таблица 1.4.1

n
e s,%	20,21	11,38	7,78	6,01	4,85	4,06	3,50	3,07	2,74	2,25	1,77	1,31

3. Эффективность полученной оценки будет определяться дисперсией СВ :

, (1.4.10)

и при больших n имеет место асимптотика

Можно указать еще один способ вычисления 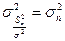. Внося в (1.4.10) под знак квадрата и используя рекуррентное свойство , получаем рекуррентное соотношение:

, , (1.4.11)

Точные значения 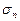приведены в табл. 1.4.2 в столбце .

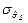4. Другой способ получения оценок параметров распределения основан на порядковых статистиках. Рассмотрим выборку непрерывной СВ объемом n, полученную при стандартных условиях из совокупности с ФР и ПР : .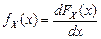

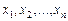Выборка, упорядоченная по возрастанию 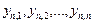, называется вариационным рядом. Член вариационного ряда с фиксированным номером называется элементарной порядковой статистикой. Каждому номеру 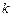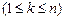соответствует случайная величина 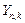с законом распределения, зависящим от Основным исходным пунктом при установлении закона распределения 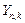служит биномиальное (точное полиномиальное) распределение дискретных случайных величин.

Используем универсальное автопреобразование 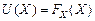(п.1.2) и рассмотрим вариационный ряд 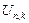, все члены которого будут сосредоточены на отрезке [0;1] (рис.1.4.1).

Рис.1.4.1. Схема расположения вариационного ряда

выборки из совокупности R(0,1)

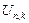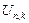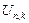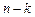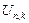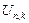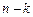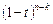Вариационный ряд , очевидно, разбивается на 3 группы: Ι содержит значение, меньшее ; ΙΙ – само значение ; ΙΙΙ – значений, больших . Пусть значение находится в точке . Тогда вероятность того, что значение окажется левее точки t составит , вероятность того, что значений окажется правее точки ,соответственно . Вероятность всей композиции будет равна произведению Количество комбинаций, реализующих точное расположение, согласно формуле полиномиального распределения (см. ссылку. на стр. 7), составит .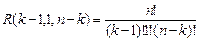

Таким образом, функция распределения 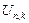составит
. (1.4.12)

Дифференцируя последнее выражение по 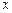и вспоминая, что 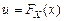, , 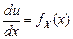получаем плотность распределения :

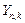, (1.4.13)

или, используя свойство биномиальных коэффициентов 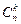, получаем тождественную форму:

. (1.4.14)

В частности, для крайних членов вариационного ряда плотность распределения получаем, полагая 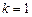- для минимального:

(1.4.15)

и - для максимального:

. (1.4.16)

В статистических приложениях большее распространение получили не сами элементарные порядковые статистики, а их композиции. Главным образом это размах и медиана выборки четного объема 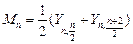, представляющие собой соответственно разность и сумму двух членов вариационного ряда (медианой выборки нечетного объема служит статистика ).

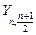Для установления законов распределения размаха и медианы необходимо знать закон совместного распределения двух элементарных порядковых статистик. Пусть их номера 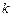и 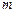. Как и в предыдущем случае, применим универсальное автопреобразование 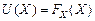и используем аналогичную схему рассуждений. В данном случае ряд окажется разбитым на 5 групп (рис. 1.4.2) численностью , , , 1, 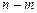соответственно.

Рис. 1.4.2. Схема расположения вариационного ряда выборки

из совокупности с двумя фиксированными членами

Рис. 1.4.3. Схема области интегрирования для определения

закона совместного распределения двух порядковых статистик

Функцию совместного распределения двух порядковых статистик получаем в виде:

.

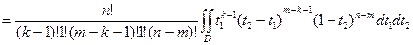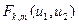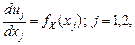Дифференцируя по и и учитывая, что , окончательно получаем плотность распределения в виде

(1.4.17)

Эту схему рассуждений очевидно можно экстраполировать на любое количество членов вариационного ряда, и ПР совместного распределения всех членов вариационного ряда будет иметь вид

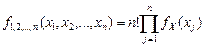, . (1.4.18)

5. Закон распределения выборочного размаха найдем как частный случай разности между двумя членами вариационного ряда: , 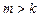. Плотность распределения разности двух случайных величин имеет вид

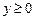, , (1.4.19)

где 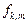–ПР совместного распределения (1.4.17).

Рассмотрим два частных случая:

межвариационный (последовательный) размах. Полагая в (1.4.19) 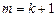, , получаем

,

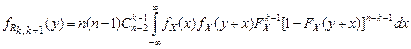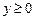, ; (1.4.20)

полный размах выборки (в дальнейшем просто размах).

Полагая в (1.4.17), (1.4.19) , , получаем

. (1.4.21)

Статистика выборки из нормальной совокупности является одной из наиболее популярных, поэтому рассмотрим ПР более детально. Как обычно в подобных случаях, рассмотрим совокупность , поскольку от не зависит, а при произвольном 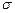размах определяется умножением на размаха выборки из (другими словами рассматривается нормированный размах 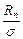выборки из произвольной нормальной совокупности).

При оговоренных условиях , Подставляя в (1.4.21), находим:

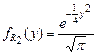, . (1.4.22)

Для 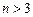точные формулы ПР существуют только в квадратуре и для больших 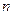нужно исследовать их асимптотическое поведение. Вид ПР для , 10 представлен на рис. 1.4.4.

Рис. 1.4.4. Плотность выборочного размаха

в зависимости от объема выборки

Асимптотика числовых характеристик нормированного размаха имеет вид

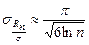, . (1.4.23)

При этом нормированный размах , очевидно, есть несмещенная оценка генерального СКО, т.е. . В свою очередь, СКО полученной оценки будет совпадать с коэффициентом вариации нормированного размаха , предельное значение которого составит

. (1.4.24)

Сравнительная эффективность оценки приведена в табл. 1.4.2. Числовые характеристики и квантили нормированного размаха 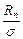даны в приложении 3.

6. При установлении закона распределения выборочной медианы рассмотрим два случая:

медиана выборки нечетного объема.

В этом случае , и медианой служит серединная порядковая статистика с номером . Подставляя параметры статистики , , получаем общий вид плотности распределения медианы нечетной выборки:

(1.4.25)

Для совокупности N(0,1) получаем

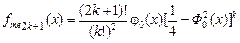; (1.4.26)

при четном объеме выборки в качестве медианы, вообще говоря, может рассматриваться любая точка из интервала 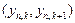. Для определенности медианой принято считать середину указанного интервала. Плотность распределения случайной величины найдем путем последовательных преобразований. Сначала найдем плотность распределения суммы, используя формулу суммы и ПР (1.4.14) и учитывая, что :

Искомую ПР медианы получим из ПР суммы:

. (1.4.27)

Для нормальной совокупности окончательно получаем

. (1.4.28)

При n =2 медиана совпадает с выборочным средним. Вид ПР медианы для n =3÷5 представлен на рис.1.4.5.

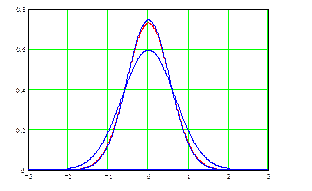
Рис. 1.4.5. Плотность распределения выборочной

медианы в зависимости от объема выборки n

При больших n для серединной порядковой статистики справедлива асимптотика

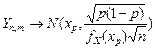, где . (1.4.29)

Таким образом, серединная порядковая статистика является асимптотически нормальной оценкой генеральной квантили при любом законе распределения . В частности, для нормальной совокупности 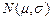выборочная медиана распределена по нормальному закону , являясь несмещенной оценкой генерального среднего. При этом оценка по медиане при больших n в раз менее эффективна, чем по выборочному среднему, у которого .

Сравнительная эффективность оценки генерального среднего нормальной совокупности по выборочной медиане в зависимости от n приведена в табл. 1.4.2.

Таблица 1.4.2. Сравнительная эффективность

точечных оценок параметров нормального распределения

n	^*)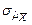
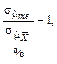
	0,707	0,707		0,756	0,756
	0,577	0,670	16,1	0,523	0,525	0,4
	0,500	0,546	9,2	0,422	0,427	1,2
	0,447	0,536	19,9	0,363	0,372	2,5
	0,408	0,463	13,5	0,323	0,335	3,7
	0,378	0,459	21,4	0,294	0,308	4,8
	0,354	0,410	15,8	0,272	0,288	5,9
	0,333	0,408	22,5	0,254	0,272	7,1
	0,316	0,372	17,7	0,239	0,259	8,4

Окончание табл. 1.4.2.

	0,258	0,319	23,6	0,191	0,217	13,6
	0,224	0,271	21,0	0,163	0,194	19,0
∞**^)			25,3

^*) Символы , 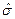означают несмещенные выборочные оценки генеральных параметров, индексы соответствуют используемой статистике.

^**) В последней строке приведен асимптотический вид СКО соответствующих статистик при больших .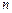

Приведенные в табл. 1.4.2 СКО используются, в частности, для определения контрольных границ при построении контрольных карт количественного признака (умножением на 3).

Глава 2. основы теории планирования эксперимента

Дата добавления: 2014-12-26