Введение. 1. Исходным понятием теории вероятностей является случайное событие – событие, которое может произойти или не произойти при воспроизводимой совокупности

1. Исходным понятием теории вероятностей является случайное событие – событие, которое может произойти или не произойти при воспроизводимой совокупности условий опыта (испытания, наблюдения). Например, появление орла при бросании монеты, выпадение 11 очков при бросании двух игральных костей, попадание в поле допуска размера очередной детали с автоматической производственной линии, существенное улучшение состояния у группы больных после лечения определенным препаратом и т.д. Из перечисленных примеров видно, что каждое событие обладает некоторой степенью возможности. В примере с монетой и игральными костями сразу можно решить, что выпадение орла более возможно, чем выпадение 11 очков при бросании двух игральных костей, а для анализа стабильности технологического процесса или действия лекарственного препарата необходимо иметь фактические результаты наблюдений. С понятием случайного события связано другое фундаментальное понятие теории вероятностей – понятие случайной величины (СВ). Под случайной величиной понимается величина, которая в опыте с несколькими возможными исходами может принимать то или иное значение. Например, число очков при бросании игральной кости, частота появления «орла» в серии повторных опытов с монетой, фактическое количественное значение параметра при контроле и испытаниях промышленной продукции, очередной результат в серии повторных измерений и т.д. Законом распределения случайной величины называется любое правило (функция), позволяющее однозначно определить вероятности возможных значений случайной величины. Наиболее просто обстоит дело, когда множество возможных значений случайной величины конечно либо счетно и может быть отождествлено с пространством событий. Например, появление любого из чисел от «1» до «6» при бросании игральной кости равновероятно с вероятностью 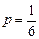; множество возможных значений частоты появления «орла» при трех бросаниях монеты составляет 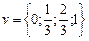с вероятностями .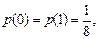

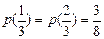Очень важную роль при анализе CB играют ее числовые характеристики, позволяющие определить ее положение на числовой оси, величину рассеивания – степень случайности и форму рассеяния. Важнейшей числовой характеристикой CB является ее среднее значение или математическое ожидание, определяемой как .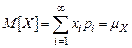

Если под 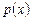понимать дискретное распределение единичной массы на тонком невесомом стержне, то среднее значение можно интерпретировать как 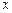– координату центра масс такой системы. Рассеивание CB около своего среднего значения характеризуется дисперсией .

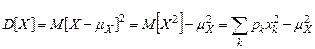В механической интерпретации 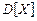есть момент инерции стержня переменной плотности относительно перпендикулярной оси, проходящей через точку 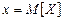. Для большей наглядности рассеивание CB характеризуют стандартным или средним квадратичным отклонением (СКО) 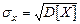, которое имеет такую же размерность, что и сама CB. Для более детального описания CB используют также асимметрию 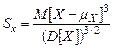и эксцесс 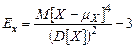. Для симметричного относительно 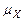плотности распределения 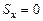, , 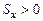если распределение быстрее стремится к нулю слева от 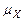, и 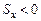– если справа. Эксцесс характеризует рассеивание CB около среднего значения по сравнению с нормальной CB, у которой E_x= 0. Из определения M [ X ] и D [ X ] вытекают их следующие свойства:

– среднее значение неслучайной величины а равно ей самой, ;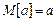

– для любой пары CB Х и Y и неслучайных чисел a и b ;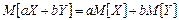

– дисперсия неслучайной величины a равна нулю, ;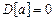

–для любой пары независимых CB 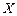и 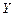и неслучайных чисел 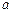и .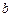

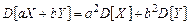2. Наиболее употребительными являются следующие виды дискретных CB. Гипергеометрическое распределение в наглядной интерпретации представляет собой распределение числа черных шаров в случайной выборке или без возвращения из корзины (числа дефектных единиц при выборочном контроле партии штучной продукции). Это распределение совпадает с законом «Спорт-лото» 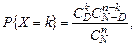где N – объем партии, D – число дефектных единиц, n – объем выборки[1]. Среднее и дисперсия гипергеометрического распределения равны:

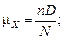
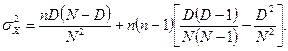
Биномиальное распределение. Рассмотрим асимптотику при 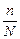<<1. Разлагая биноминальные коэффициенты через факториалы, получим .

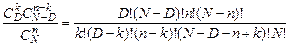После группировки сомножителей и выделения 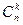, будем иметь 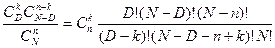. Попарно сокращая факториалы числителя и знаменателя, преобразуем последнее выражение к виду

.

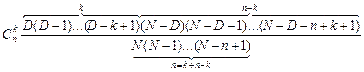Откуда получаем асимптотику 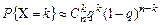, где .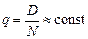

В чистом виде биноминальное распределение возникает в выборке с возвращением, когда вероятность успеха каждого испытания не зависит от результатов других испытаний и является величиной постоянной.Числовые характеристики биномиального распределения имеют вид: ; .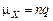

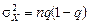В предельном случае, когда количество опытов n в испытаниях неограниченно возрастает, а вероятность успеха q неограниченно убывает, но так, что их произведение 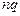имеет конечный предел: .

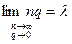Перепишем биномиальный закон в виде

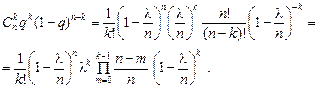
Первые три сомножителя на основании второго замечательного предела дадут 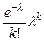. Последний сомножитель при конечном k стремится к 1. Логарифмируя оставшийся сомножитель, получим

.

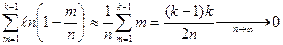Таким образом, для распределения числа редких событий получаем асимптотику в виде распределения Пуассона: .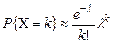

Помимо рассмотренного «предельного» случая, распределение Пуассона (распределение вероятностей редких событий) является одним из фундаментальных результатов во многих других приложениях теории вероятностей (теория надежности, теория случайных процессов и т.д.). У пуассоновской CB среднее и дисперсия равны между собой: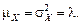

3. Муавр, а позднее независимо от него Лаплас исследовали биномиальное распределение при больших n и установили приближенную формулу (теорема Муавра-Лапласа):

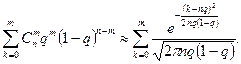
При этом дискретные точки нормированной CB 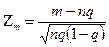располагаются на числовой оси настолько тесно, что ряд в функции распределения можно заменить интегралом:

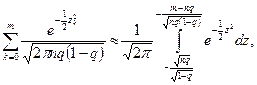где ,

а нижний предел в интеграле при больших 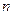можно положить равным – ¥.

Функция, стоящая под интегралом 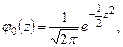называется плотностью распределения стандартной нормальной случайной величины.

Функцию распределения CB 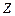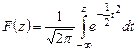удобнее представить в ви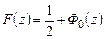де , где 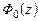– функция Лапласа,

или интеграл вероятностей, определяется уравнением

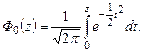
Таким образом, можно осуществить переход от дискретных CB к непрерывным, важнейшей из которых является именно нормальная CB.

Плотность распределения и числовые характеристики CB X, связанной с CB Z отношением X =s Z +m, имеют следующий вид:

; ;

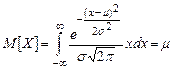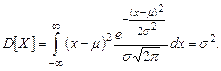
Глава 1. Теоретические основы статистического моделирования случайных процессов

Дата добавления: 2014-12-26