
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема Кронекера-Капелли
Ранг матрицы. Элементарные преобразования матрицы
Обратная матрица
Транспонирование матриц
Матрицы. Основные операции над матрицами
Задача 1.6. Найдите  , если
, если  ,
,  .
.
Ответ:  .
.
Задача 1.7. Найдите произведение 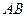 матриц
матриц
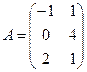 и
и  . Ответ:
. Ответ: 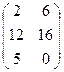 .
.
Задача 1.8. Проверьте, выполняются ли равенства  ,
,  для матриц:
для матриц:
 ,
, 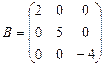 ,
,  .
.
Ответ: равенства верны.
Задача 1.9. Вычислите  , если
, если
 ,
,  ,
,  . Ответ:
. Ответ:  .
.
Задача 1.10. Проверьте, что матрица 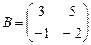 является обратной к матрице
является обратной к матрице  .
.
Задача 1.11. Найдите 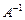 для матрицы
для матрицы
 . Ответ:
. Ответ:  .
.
Задача 1.12. Приведите к ступенчатому виду матрицы  ,
,  . Найдите их ранги.
. Найдите их ранги.
Ответ:  ;
; 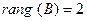 .
.
 МОДУЛЬ 2. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ
МОДУЛЬ 2. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ

Пусть задана система из  линейных уравнений с
линейных уравнений с  неизвестными
неизвестными  :
:
 (1)
(1)
 где числа
где числа  называются коэффициентами системы,
называются коэффициентами системы,

 а числа
а числа 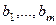 — свободными членами.
— свободными членами.
Решением системы (1) называется такой набор чисел 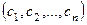 , что при его подстановке в систему вместо соответствующих неизвестных (
, что при его подстановке в систему вместо соответствующих неизвестных ( вместо
вместо  ,…,
,…,  вместо
вместо  ) каждое из уравнений системы обращается в тождество.
) каждое из уравнений системы обращается в тождество.
 Совместной называется система, которая имеет хотя бы одно решение.
Совместной называется система, которая имеет хотя бы одно решение.

 Несовместной называется система, которая не имеет ни одно го решения.
Несовместной называется система, которая не имеет ни одно го решения.
 Определённой называется система, которая имеет единственное решение.
Определённой называется система, которая имеет единственное решение.
 Неопределённой называется система, которая имеет более одного решения.
Неопределённой называется система, которая имеет более одного решения.
 Однородной называется система, если
Однородной называется система, если 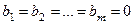 . В противном случае система называется неоднородной.
. В противном случае система называется неоднородной.
Матрицей системы называется матрица, составленная из коэффициентов системы:


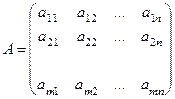 .
.
Расширенной матрицей системы называется матрица


 .
.
 Теорема Кронекера-Капелли. Cистема линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы:
Теорема Кронекера-Капелли. Cистема линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы:

 Исследовать систему линейных уравнений означает определить, совместна она или нет, а для совместной системы — выяснить, определённа она или нет. При этом возможны три варианта:
Исследовать систему линейных уравнений означает определить, совместна она или нет, а для совместной системы — выяснить, определённа она или нет. При этом возможны три варианта:
1) Если  , то система несовместна. (*)
, то система несовместна. (*)

 2) Если
2) Если 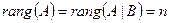 , где
, где  — число неизвестных, то система совместна и определённа. (**)
— число неизвестных, то система совместна и определённа. (**)
3) Если 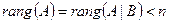 , то система совместна и неопределённа. (***)
, то система совместна и неопределённа. (***)

 § 2. Решение систем линейных уравнений
§ 2. Решение систем линейных уравнений
Метод Крамера
 Пусть система из
Пусть система из  линейных уравнений с
линейных уравнений с  неизвестными записана в матричной форме:
неизвестными записана в матричной форме:  , где
, где  — матрица системы,
— матрица системы,
 — столбец неизвестных,
— столбец неизвестных, 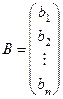 — столбец свободных членов.
— столбец свободных членов.
Пусть  — определитель матрицы
— определитель матрицы 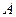 и пусть
и пусть 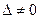 , т.е.
, т.е.


 Правило Крамера. Если определитель системы (1) Правило Крамера. Если определитель системы (1) 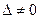 , то эта система совместна и определённа, т.е. имеет единственное решение, получаемое по формулам: , то эта система совместна и определённа, т.е. имеет единственное решение, получаемое по формулам:
 , ,  где
где 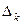 — определитель, получаемый из определителя — определитель, получаемый из определителя  заменой заменой 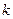 -го столбца на столбец свободных членов. -го столбца на столбец свободных членов.
|
Пример 2.1. Решите систему уравнений по формулам Крамера:

 Найдём определитель матрицы системы:
Найдём определитель матрицы системы:  .
.
Т.к. 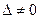 , то решение системы существует и единственно.
, то решение системы существует и единственно.
Найдём определитель  . В определитель
. В определитель  вместо первого столбца
вместо первого столбца  подставим столбец свободных членов
подставим столбец свободных членов  :
:
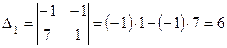 .
.
Определитель  получается из
получается из  подстановкой столбца свободных членов
подстановкой столбца свободных членов  вместо второго столбца
вместо второго столбца  :
:
 .
.
Отсюда получим решение системы уравнений:
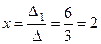 ;
; 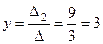 .
.
 Ответ:
Ответ: 
 Матричный метод
Матричный метод
 Пусть система из
Пусть система из  линейных уравнений с
линейных уравнений с  неизвестными записана в матричной форме:
неизвестными записана в матричной форме:  , Тогда, если определитель
, Тогда, если определитель 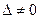 , то система совместна и определённа, её решение задаётся формулой:
, то система совместна и определённа, её решение задаётся формулой:

Пример 2.2. Решите систему уравнений примера 2.1 с помощью обратной матрицы:  .
.
1)  Т.к.
Т.к.  , то решение системы существует и единственно.
, то решение системы существует и единственно.
2) Найдём алгебраические дополнения к элементам матрицы  :
: 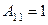 ,
,  ,
,  ,
, 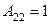 .
.
3) Найдём присоединённую матрицу: 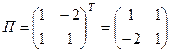 .
.
4) Найдём матрицу 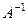 :
:  .
.
5) Найдём решение системы уравнений:
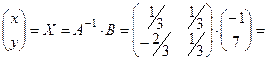
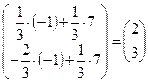 .
.
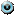 Ответ:
Ответ:  .
.
Пример 2.3. Решите систему уравнений по формулам Крамера и с помощью обратной матрицы: 
 I способ, метод Крамера.
I способ, метод Крамера.

 .
.

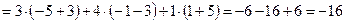 .
.
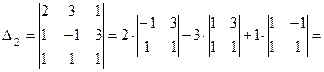
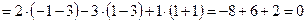 .
.

 .
.
 ,
, 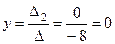 ,
,  .
.
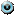 Ответ:
Ответ: 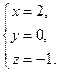
 II способ, метод обратной матрицы.
II способ, метод обратной матрицы.
1)  .
.
2) 
Алгебраические дополнения элементов матрицы 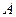 :
:


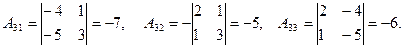
3) Присоединенная матрица:
 .
.
4) Обратная матрица:
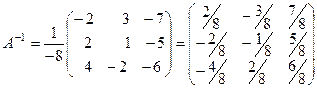 .
.
5) Решение системы:
 .
.

 Ответ:
Ответ: 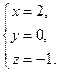
Метод Гаусса решения систем линейных уравнений.
 Процесс решения по методу Гаусса состоит из двух этапов.
Процесс решения по методу Гаусса состоит из двух этапов.
На первом этапе система (1) приводится к одной из следующих систем:
· 
 (2)
(2)
где  ,
,  .
.
· 
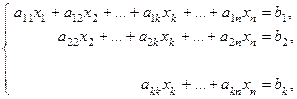 (3)
(3)
где  .
.
· 
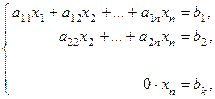 (4)
(4)
 где
где 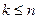 .
.
На втором этапе:
· система (2) имеет единственное решение, значение  находится из последнего уравнения, значение
находится из последнего уравнения, значение  — из предпоследнего,…,значение
— из предпоследнего,…,значение  — из первого;
— из первого;
· система (3) имеет бесконечное множество решений;
· система (4) несовместна, так как никакие значения неизвестных не могут удовлетворять её последнему уравнению.
 Метод Гаусса. применим к любой (!) системе линейных уравнений. Метод Гаусса. применим к любой (!) системе линейных уравнений.
|
Опишем метод Гаусса подробнее на примере.
Пример 2.4. Исследуйте систему линейных уравнений примера 2.1; и если она совместна, то найдите её решение: 
 I. Исследуем систему на совместность. Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:
I. Исследуем систему на совместность. Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:
 ~
~  .
.
Очевидно, что 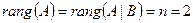 . Значит, согласно (**) (см. §1), система совместна и определённа, т.е. существует единственное решение.
. Значит, согласно (**) (см. §1), система совместна и определённа, т.е. существует единственное решение.
II. Найдём решение системы. Запишем систему уравнений, соответствующую полученной расширенной матрице: 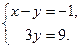 Имеем систему вида (2). Из второго уравнения
Имеем систему вида (2). Из второго уравнения 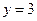 . Подставляя это значение в первое уравнение, получим:
. Подставляя это значение в первое уравнение, получим: 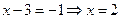 .
.
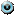 Ответ:
Ответ: 
Пример 2.5. Исследуйте систему линейных уравнений примера 2.3, и если она совместна, то найдите её решение: 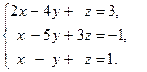
 I. Исследуем систему на совместность. Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:
I. Исследуем систему на совместность. Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:
 ~
~  ~
~
~  .
.
Очевидно, что 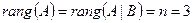 . Значит, согласно (**) (см. §1), система совместна и определённа, т.е. существует единственное решение.
. Значит, согласно (**) (см. §1), система совместна и определённа, т.е. существует единственное решение.
II. Найдём решение системы. Запишем систему уравнений, соответствующую полученной расширенной матрице: 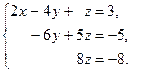
Имеем систему вида (2). Из третьего уравнения 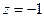 .
.
Подставляя это значение во второе уравнение, получим:  .
.
Подставляя найденные значения  в первое уравнение, получим:
в первое уравнение, получим: 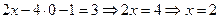 .
.
 Ответ:
Ответ: 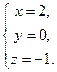
Пример 2.6. Исследуйте систему линейных уравнений, и если она совместна, то найдите её решение: 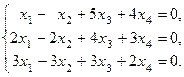
 I. Исследуем систему на совместность. Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:
I. Исследуем систему на совместность. Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:
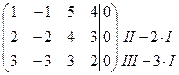 ~
~  ~~
~~  .
.
Очевидно, что  . Значит, согласно (***) (см. §1), система совместна и неопределённа, т.е. имеет бесконечно много решений.
. Значит, согласно (***) (см. §1), система совместна и неопределённа, т.е. имеет бесконечно много решений.
II. Найдём решение системы. Запишем систему уравнений, соответствующую полученной расширенной матрице:
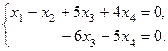
Имеем систему вида (3). Выразим  из второго уравнения и подставим полученное выражение в первое уравнение:
из второго уравнения и подставим полученное выражение в первое уравнение:
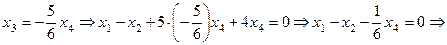
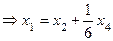 .
.
Следовательно, исходная система имеет решение 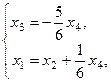 где
где  ,
, 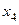 могут принимать любые действительные значения.
могут принимать любые действительные значения.
 Ответ:
Ответ: 
| Продукт | Сырье | |
| I | II | |

| 1,5 | |

| ||
| Запасы |
Пример 2.7. Цех выпускает два вида продукции  и
и  , полностью используя для их производства сырье вида I и вида II. В таблице указано число единиц сырья I и II, необходимых для производства одной единицы продукции
, полностью используя для их производства сырье вида I и вида II. В таблице указано число единиц сырья I и II, необходимых для производства одной единицы продукции  и
и  , а также имеющиеся запасы сырья.
, а также имеющиеся запасы сырья.
Может ли цех удовлетворить заказ трёх торговых организаций:
| Продукт | Заказ I организации | Заказ II организации | Заказ III организации |

| |||

|
 Пусть
Пусть  и
и  — количество единиц продукции
— количество единиц продукции  и
и  соответственно, которое может выпустить цех при данных условиях производства. Тогда данные первой таблицы можно представить системой уравнений:
соответственно, которое может выпустить цех при данных условиях производства. Тогда данные первой таблицы можно представить системой уравнений: 
Решим её методом Гаусса.
 ~
~ 
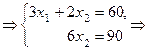


Т.е. цех произведёт 10 единиц продукта  , 15 единиц — продукта
, 15 единиц — продукта  .
.
Выясним, сможет ли цех выполнить заказ.
 Для выполнения заказа нужно
Для выполнения заказа нужно 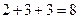 единиц продукта
единиц продукта  и
и  единиц продукта
единиц продукта  . Следовательно, цех может выполнить заказ.
. Следовательно, цех может выполнить заказ.
ЧТО ДОЛЖЕН ЗНАТЬ СТУДЕНТ
1. Понятие системы  линейных уравнений с
линейных уравнений с  неизвестными.
неизвестными.
2. Матричный способ решения системы уравнений (метод обратной матрицы).
3. Метод Крамера решения систем уравнений.
4. Метод Гаусса решения систем уравнений.
5. Понятие однородных систем уравнений.
6. Теорема Кронекера-Капелли.
|
|
Дата добавления: 2014-12-26; Просмотров: 812; Нарушение авторских прав?; Мы поможем в написании вашей работы!