
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства (четность, периодичность, монотонность, ограниченность) и графики функций
|
|
|
|
Функция, область ее определения и способы задания. Сложные и обратные функции.
ФУНКЦИЯ - соответствие y = f (x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента, или независимого переменного) соответствует определенное значение другой величины y (зависимой переменной, или функции).
Переменная y называется функцией переменной x, если каждому допустимому значению х соответствует определенное значение y.
Символически функциональная зависимость между переменной y (функцией) и переменной х (аргументом) записывается с помощью равенства y = f(x), где f обозначает совокупность действий, которые надо произвести над х, чтобы получить y.
Областью определения (существования) функции D(y) называется множество всех действительных значений аргумента х (множество всех точек числовой оси), при которых она имеет действительное значение.
Для задания функции необходимо и достаточно знать закон соответствия f, по которому для каждого значения аргумента можно указать единственное значение функции и область определения D(y).
Способы задания функций
Функция может быть задана:
Аналитически (формулой): зависимость между аргументом и функцией задается в виде математической формулы. В этой формуле указаны действия, которые нужно произвести над значением аргумента, чтобы получить соответствующее значение функции.
Таблицей: значения аргумента и соответствующие им значения функции записаны в виде таблицы.
Графиком: совокупность точек плоскости, абсциссы которых являются значениями независимой переменной, а ординаты – соответствующими значениями функции, называется графиком данной функции.
|
|
|
Сложная функция.
Пусть функция  определена на множестве
определена на множестве 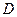 , а функция
, а функция 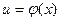 на множестве
на множестве  , причем для
, причем для 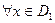 соответствующее значение
соответствующее значение 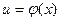
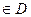 . Тогда на множестве
. Тогда на множестве  определена функция
определена функция 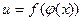 , которая называется сложной функцией от
, которая называется сложной функцией от 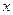 (или суперпозицией заданных функций, или функцией от функции).
(или суперпозицией заданных функций, или функцией от функции).
Переменную 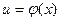 называют промежуточным аргументом сложной функции.
называют промежуточным аргументом сложной функции.
Например, функция 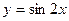 есть суперпозиция двух функций
есть суперпозиция двух функций  и
и  . Сложная функция может иметь несколько промежуточных аргументов.
. Сложная функция может иметь несколько промежуточных аргументов.
Обратная функция.
Пусть задана функция  с областью определения
с областью определения 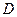 и множеством значений Е. если каждому значению
и множеством значений Е. если каждому значению 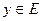 соответствует единственное значение
соответствует единственное значение 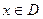 , то определена функция
, то определена функция 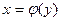 с областью определения Е и множеством значений
с областью определения Е и множеством значений 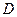 . Такая функция
. Такая функция 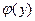 называется обратной к функции
называется обратной к функции 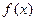 и записывается в следующем виде:
и записывается в следующем виде: 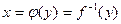 . Про функции
. Про функции  и
и 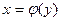 говорят, что они являются взаимно обратными. Чтобы найти функцию
говорят, что они являются взаимно обратными. Чтобы найти функцию 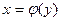 , обратную к функции
, обратную к функции  , достаточно решить уравнение
, достаточно решить уравнение  относительно
относительно 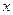 (если это возможно).
(если это возможно).
Пример. Для функции 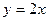 обратной функцией является функция
обратной функцией является функция 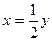 ;
;
Пример. Для функции  , обратной функцией является
, обратной функцией является 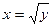 ; заметим, что для функции
; заметим, что для функции 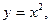 заданной на отрезке
заданной на отрезке 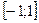 , обратной не существует, т.к. одному значению
, обратной не существует, т.к. одному значению 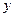 соответствует два значения
соответствует два значения 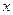 .
.
Из определения обратной функции вытекает, что функция  имеет обратную тогда и только тогда, когда функция
имеет обратную тогда и только тогда, когда функция 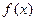 задает взаимно однозначное соответствие между множествами
задает взаимно однозначное соответствие между множествами 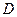 и Е. отсюда следует, что любая строго монотонная функция имеет обратную. При этом если функция возрастает (убывает), то обратная функция также возрастает (убывает).
и Е. отсюда следует, что любая строго монотонная функция имеет обратную. При этом если функция возрастает (убывает), то обратная функция также возрастает (убывает).
Заметим, что функция  и обратная ей
и обратная ей 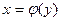 изображаются одной и той же кривой, т.е. графики их совпадают. Если же условиться, что, как обычно, независимую переменную (т.е. аргумент) обозначить через
изображаются одной и той же кривой, т.е. графики их совпадают. Если же условиться, что, как обычно, независимую переменную (т.е. аргумент) обозначить через 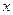 , а зависимую переменную через
, а зависимую переменную через 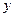 , то функция обратная функции
, то функция обратная функции  запишется в виде
запишется в виде 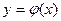 .
.
Графики взаимно обратных функций  и
и 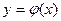 симметричны относительно биссектрисы первого и третьего координатных углов.
симметричны относительно биссектрисы первого и третьего координатных углов.
|
|
|
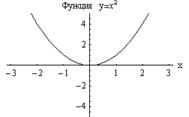
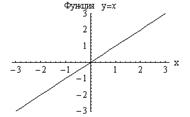 1. Функция
1. Функция  , определенная на множестве
, определенная на множестве 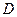 , называется четной, если
, называется четной, если  выполняются условия
выполняются условия  и
и 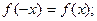 нечетной, если
нечетной, если  выполняются условия
выполняются условия  и
и 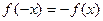 .
.
График четной функции симметричен относительно оси  , а нечетной – относительно начала координат.
, а нечетной – относительно начала координат.
Например, 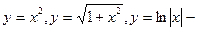 четные функции; а
четные функции; а 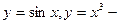 нечетные функции;
нечетные функции;  функции общего вида, т.е. не четные и не нечетные.
функции общего вида, т.е. не четные и не нечетные.
 2. Функция
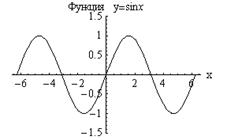
2. Функция  , определенная на множестве
, определенная на множестве 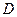 , называется периодической на этом множестве, если существует такое число
, называется периодической на этом множестве, если существует такое число 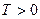 , что при каждом
, что при каждом 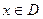 значение
значение 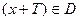 и
и 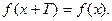 При этом число
При этом число 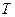 называется периодом функции. Если
называется периодом функции. Если 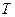 - период функции, то ее периодами будут также числа
- период функции, то ее периодами будут также числа  , где
, где 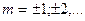 Так, для
Так, для 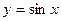 периодами будут числа
периодами будут числа 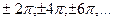 Основной период (наименьший положительный) – это период
Основной период (наименьший положительный) – это период  . Вообще обычно за основной период берут наименьшее положительное число
. Вообще обычно за основной период берут наименьшее положительное число 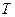 , удовлетворяющее равенству
, удовлетворяющее равенству 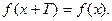
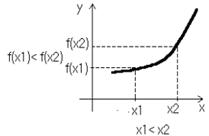
3. Функция y=f(x) называется возрастающей на некотором интервале если для любых х из этого интервала большему значению аргумента соответствует большее значение функции, т.е. при 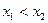 имеет место неравенство f(x1)<f(x2).
имеет место неравенство f(x1)<f(x2).
 Функция y=f(x) называется невозрастающей, если на некотором интервале
Функция y=f(x) называется невозрастающей, если на некотором интервале 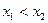 имеет место неравенство f(x1)≥f(x2).
имеет место неравенство f(x1)≥f(x2).
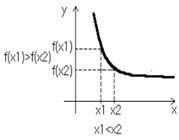
Функцияy=f(x) называется убывающей на некотором интервале, если для любых х из этого интервала большему значению аргумента соответствует меньшее значение функции, т.е. при 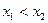 имеет место неравенство f(x1)>f(x2).
имеет место неравенство f(x1)>f(x2).
Функция y=f(x) называется неубывающей, если на некотором интервале 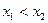 имеет место неравенство f(x1)≤f(x2).
имеет место неравенство f(x1)≤f(x2).
Функции только убывающие или только возрастающие называются монотонными.
4. Функцию  , определенную на множестве
, определенную на множестве 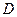 , называют ограниченной на этом множестве, если существует такое число
, называют ограниченной на этом множестве, если существует такое число 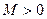 , что для всех
, что для всех 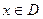 выполняется неравенство
выполняется неравенство 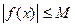 (короткая запись:
(короткая запись:  ,
, 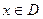 , называется ограниченной на
, называется ограниченной на 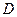 , если
, если  ). Отсюда следует, что график ограниченной функции лежит между прямыми
). Отсюда следует, что график ограниченной функции лежит между прямыми 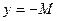 и
и  .
.

|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 4214; Нарушение авторских прав?; Мы поможем в написании вашей работы!