Комплексные показатели надежности

Показателем, определяющим долговечность системы, объекта, машины, может служить коэффициент технического использования.

Коэффициент технического использования — отношение математического ожидания суммарного времени пребывания объекта в работоспособном состоянии за некоторый период эксплуатации к математическому ожиданию суммарного времени пребывания объекта в работоспособном состоянии и всех простоев для ремонта и технического обслуживания:

Коэффициент технического использования, взятый за период между плановыми ремонтами и техническим обслуживанием, называется коэффициентом готовности, который оценивает непредусмотренные остановки машины и что плановые ремонты и мероприятия по техническому обслуживанию не полностью выполняют свою роль.

Коэффициент готовности — вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается. Физический смысл коэффициента готовности - это вероятность того, что в прогнозируемый момент времени изделие будет исправно, т.е. оно не будет находиться во внеплановом ремонте.

Коэффициент оперативной готовности — вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается, и, начиная с этого момента, будет работать безотказно в течение заданного интервала времени.

Классификация показателей. В зависимости от способа получения показатели подразделяют на:

· расчетные, получаемые расчетными методами;

· экспериментальные, определяемые по данным испытаний;

· эксплуатационные, получаемые по данным эксплуатации.

В зависимости от области использования различают показатели надежности нормативные и оценочные.

Нормативными называют показатели надежности, регламентированные в нормативно-технической или конструкторской документации.

К оценочным относят фактические значения показателей надежности опытных образцов и серийной продукции, получаемые по результатам испытаний или эксплуатации.

3. Математические зависимости для оценки надежности

3.1. Функциональные зависимости надежности

Отказы, возникающие в процессе испытаний или эксплуатации, могут быть вызваны неблагоприятным сочетанием различных факторов — рассеянием действующих нагрузок, отклонением от номинального значения механических характеристик материалов, неблаго­приятным сочетанием допусков в местах сопряжения и т. п. Поэтому в расчетах надежности различные параметры рассматривают как случайные величины, которые могут принимать то или иное значение, неизвестное заранее.

Различают случайные величины прерывного (дискретного) и непрерывного типов. Ус­ловимся случайные величины в дальнейшем обозначать большими буквами, а их возможные значения — соответствующими малыми. Для каждого числа х в диапазоне изменения слу­чайной величины Х существует определенная вероятность Р(Х<х) того, что Х не превышает значения х. Вероятность этого события называют функцией распределения:

F(Х) = Р(Х<х). (3.1)

Функция распределения — универсальная характеристика, так как она является функ­цией как непрерывных, так и дискретных случайных величин. Функция (х) относится к не­убывающим функциям — х монотонно возрастает при непрерывных процессах и ступенчато возрастает при дискретных процессах. В пределах изменения случайной величины Х эта функция изменяется от 0 до 1: F(-oo) = 0; F(oo) = 1;

Производную от функции распределения по текущей переменной называют плотно­стью распределения

(3.2)

которая характеризует частоту повторений данного значения случайной величины. В теории надежности величину f(x) называют плотностью вероятности. Плотность распределения есть неотрицательная функция своего аргумента f(x) > 0.

Интеграл в бесконечных пределах от плотности распределения равен единице:

В ряде случаев в качестве характеристик распределения случайных величин достаточно использовать некоторые числовые величины, среди которых в теории надежности наиболее употребительными являются математическое ожидание (среднее значение), мода и медиана (характеризуют положение центров группирования случайных величин на числовой оси), дисперсия, среднее квадратическое отклонение и коэффициент вариации (характеризуют рассеяние случайной величины). Значения характеристик, полученные по результатам испы­таний или эксплуатации, называют статистическими оценками. Характеристики распреде­ления используют для прогнозирования надежности.

Для дискретных случайных величин математическое ожидание M_x равно сумме про­изведений всех возможных значений Х на вероятности этих значений:

(3.3)

Математическое ожидание для непрерывной случайной величины выражается интегра­лом в бесконечных пределах от произведения непрерывно изменяющихся возможных значе­ний случайной величины на плотность распределения

(3.4)

Математическое ожидание случайной величины непосредственно связано с ее средним значением. При неограниченном увеличении числа опытов среднее арифметическое значе­ние величины х приближается к математическому ожиданию и называется оценкой среднего значения:

(3.5)

где n - общее число опытов; x_t - текущее значение случайной величины.

Дисперсией (D) случайной величины называют математическое ожидание квадрата от­клонения этой величины от ее математического ожидания.

Для дискретной случайной величины дисперсия равна:

(3.6)

Для непрерывной случайной величины дисперсия определяется из выражения

(3.7)

Оценка дисперсии случайной величины:

(3.8)

Дисперсия случайной величины является характеристикой рассеяния — разбросанности значений случайной величины около ее математического ожидания. Размерность дисперсии соответствует квадрату размерности случайной величины. Для наглядности в качестве ха­рактеристики рассеяния удобнее использовать величину, размерность которой совпадает с размерностью случайной величины. Такой характеристикой может быть среднее квадратическое отклонение σ_х, которое определяется как корень квадратный из дисперсии:

(3.9)

Для оценки рассеяния с помощью безразмерной величины используют коэффициент вариации, который равен:

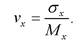(3.10)

Модой случайной величины называют ее наиболее вероятное значение или то ее значе­ние, при котором плотность вероятности максимальна.

Медиана характеризует расположение центра группирования случайной величины. Площадь под графиком функции плотности распределения делится медианой пополам.

Квантиль — значение случайной величины, соответствующее заданной вероятности. Квантиль, соответствующую вероятности 0,5, называют медианой.

Аналогично предыдущим характеристикам понятия моды и медианы даны в статисти­ческой трактовке. Для симметричного модального (т.е. имеющего один максимум)распреде­ления математическое ожидание, мода и медиана совпадают.

Рассматривая случаи появления или отсутствия события А в большом числе испытаний, можно установить определенные закономерности появления этого события. Если при прове­дении n₁ испытаний событие А имело место т₁ раз, то относительную частоту появления события А определяют из соотношения

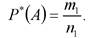(3.11)

Если событие А имело место в каждом из n₁, испытаний, т. е. m₁ = n₁, то Р*(А) = 1. Если событие А не наступило ни в одном из n₁, испытаний, т. е. m₁= 0, то Р*(А)=0. При проведе­нии серии последовательных испытаний получим соотношения:

Относительная частота становится более устойчивой при увеличении числа испытаний. Такая закономерность была замечена давно и подтверждена результатами решения различ­ных примеров. Самыми известными примерами являются примеры бросания монеты или иг­ральной кости. Так, при большом числе бросании монеты относительная частота выпадания герба равна 1/2 и равна относительной частоте выпадания цифры. При большом числе бро­саний игральной кости относительная частота выпадания каждой стороны, на которой изо­бражены цифры от 1 до 6, равна 1/6.

Приведенные примеры показывают, что существует постоянная величина (в нашем случае 1/2 или 1/6), около которой колеблется относительная частота свершения случайного события и к которой она все более приближается с увеличением числа испытаний. Постоян­ную величину, к которой приближается относительная частота случайного события, называ­ют вероятностью случайного события А и обозначают символом Р(А). На практике при большом числе испытаний вероятность случайного события приближенно принимают рав­ной относительной частоте этого события:

Р(А) = Р(А).

Математическим основанием этого утверждения является закон больших чисел (Я. Бер-нулли) - вероятность отклонения относительной частоты некоторого события А от вероятно­сти Р(А) этого события более чем на произвольно заданную величину s > 0 становится сколь угодно малой, если число испытаний n неограниченно возрастает.

Таким образом, вероятность события Р(А) представляет собой число, заключенное в интервале от нуля до единицы, т. е. справедливо неравенство

0 < P(A)< 1. (3.12)

3.2. Теорема сложения вероятностей

События могут быть совместными и несовместными. Два события называют несовме­стными, если в результате опыта они не могут появиться одновременно. И наоборот, собы­тия считаются совместными, если они появляются одновременно в результате такого опыта.

Вероятность суммы двух несовместных событий равна сумме вероятностей этих со­бытий

Р(А+В)=Р(А)+Р(В). (3.13)

Метод полной индукции позволяет использовать теорему сложения для произвольного числа несовместных событий. Так, вероятность суммы нескольких событий равна сумме ве­роятностей этих событий

P(A 1 +A2+...+An)=P(A 1)+P(A2)+...+P(A„). (3.14)

Более удобная запись теоремы сложения:

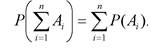(3.15)

С л е д с т в и е 1. Если события А₁, А₂,..., А_п образуют полную группу несовместных событий, то сумма их вероятностей равна единице:

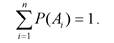(3.16)

Противоположными событиями называют два несовместных события, образующих полную группу.

С л е д с т в и е 2. Сумма вероятностей противоположных событий равна единице:

Р(А) +P(A) =1 (3.17)

где А — событие, противоположное событию А.

Вероятность суммы двух совместных событий А и В выражается формулой

Р(А+В)=Р(А)+Р(В) - Р(АВ). (3.18)

Аналогично вероятность суммы трех совместных событий определяется выражением

Р(А +В +C) = Р(А) +Р(В) +Р(С) -Р(АВ) - Р(АС) -Р(ВС) +Р(АВС). (3.19)

Вероятность суммы любого числа совместных событий определяется выражением

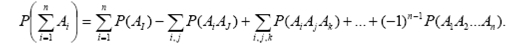(3.20)

Формула (3.20) выражает вероятность суммы любого числа событий через вероятности произведений этих событий, взятых по одному, по два, по три и т. д.

Аналогичную формулу можно написать для произведения двух событий:

Р(АВ)=Р(А)+Р(В)-Р(А+В); (3.21)

для произведения трех событий:

Р(АВС)=Р(А)+ Р(В)+ Р(С -Р(А +В) -Р(А +С) -Р(В+С)+Р(А +В+С). (3.22)

Общая формула, выражающая вероятность произведения произвольного числа собы­тий через вероятности сумм этих событий, взятых по одному, по два, по три и т. д., имеет

вид:

(3.23)

Формулы (3.20) и (3.23) находят практическое применение при преобразовании раз­личных выражений, содержащих вероятности сумм и произведений событий. В зависимости от специфики задачи в некоторых случаях удобнее бывает использовать только суммы, а в других только произведения событий.

3.3. Теорема умножения вероятностей

События могут быть независимыми и зависимыми.

Событие А называют независимым от события В, если вероятность события А не зави­сит от того, произошло событие В или нет.

Событие А называют зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Вероятность события А до того, как станет известно что-либо о событии В, равна 2/3. Если стало известно, что событие В произошло, то вероятность события А становится равной 1/2, из чего заключаем, что событие А зависит от события В.

Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается Р(А/В).

Для условий примера Р(А) = 2/3, Р(А/В) = 1/2.

Теорема умножения вероятностей формулируется следующим образом.

Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место, т. е.

Р(АВ)=Р(А)Р(В/А). (3.24)

Очевидно, что при применении теоремы умножения безразлично, какое из событий — А или В — считать первым, а какое вторым, и теорему можно записать так:

Два события называют независимыми, если появление одного из них не изменяет веро­ятности появления другого.

Понятие независимых событий может быть распространено на случай произвольного числа событий. Несколько событий называют независимыми, если любое из них не зависит от любой совокупности остальных.

Вероятность произведения двух независимых событий равна произведению вероятно­стей этих событий. Теорема умножения вероятностей может быть обобщена на случай про­извольного числа событий. В общем виде она формулируется так.

Вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляют при условии, что все предыдущие имели место:

P(A1*A2* An)=P(A1) P(A/А1) P(A3/A1*A2) P(A/А1A2* *An - 1). (3.25)

В случае независимых событий теорема упрощается и принимает вид:

_n

P(A1A2...An) = å P(A1) P(A2)...P(An), (3.26)

ⁱ⁼¹

т. е. вероятность произведения независимых событий равна произведению вероятностей этих событий.

Применяя знак произведения, теорему можно записать так:

(3.27)

Пример 3.9. Устройство состоит из пяти приборов, каждый из которых, независимо от других, может в течение времени t отказать. Отказ хотя бы одного прибора приводит к отка­зу устройства. За время t вероятность безотказной работы A₁A₂A₃ + A₁A₂A₃ + A₁A₂A₃,

где A₁, A₂, A₃ - попадания при первом - третьем выстрелах; A₁, A₂, A₃ - промах при первом -третьем выстрелах.

Вероятность каждого варианта находим по теореме умножения, а затем используем теорему сложения:

Р(В) = Р(А1)Р(А2)Р(А3) + Р(А1)Р(А2)Р(А3) + Р(А1)Р(А2)Р(А3)+ +Р(А1)Р(А2)Р(А) +

Р(А1)Р(А2)Р(А3) + Р(А1)Р(А2)Р(А3) + + Р(А_х)Р(Аг)Р(А3) = 0,8*0,6*0,3+0,8*0,6*(1-0,3)+0,8* (1-0,6)*0.3 +(1 - 0,8)*0,6*03 + 0,8*(1 - 0,6)*(1 - 0,3) + (1 - 0,8)*0,6*(1 - 0,3) +(1- 0,8)*(1 -0,6)*0,3=0,946.

4.4. Формула полной вероятности

Следствием обеих основных теорем - теоремы сложения вероятностей и теоремы ум­ножения вероятностей - является формула полной вероятности.

Пусть требуется определить вероятность некоторого события А, которое может про­изойти вместе с одним из событий: Н₁, Н₂,..., Н_п, образующих полную группу несовместных событий, называемых гипотезами. Докажем, что в этом случае

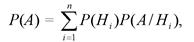(3.28)

т. е. вероятность события А вычисляется как сумма произведений вероятности каждой гипо­тезы на вероятность события при этой гипотезе.

Формулу (3.28) называют формулой полной вероятности, что можно доказать следую­щим образом.

Гипотезы Н₁,Н₂,...,Н_п образующих полную группу, поэтому событие А может появиться только в комбинации с какой-либо из этих гипотез, т. е.

А=НА+ Н2А+...+ НпА.

Так как гипотезы Н₁, Н₂,...,Н_п несовместны, то и комбинации Н₁А + Н₂А+...+ Н_пА так­же несовместны. Применяя теорему сложения, получим для этих гипотез:

Применяя к событию НА теорему умножения, получим

что и требовалось доказать.

Пример 3.11. По движущемуся танку производят три выстрела из артиллерийского орудия. Вероятность попадания при первом выстреле равна 0,5; при втором - 0,7; при треть­ем - 0,8. Для вывода танка из строя заведомо достаточно трех попаданий. При одном попада­нии танк выходит из строя с вероятностью 0,3; при двух попаданиях - с вероятностью 0,9. Определить вероятность того, что в результате трех выстрелов танк выйдет из строя.

Р е ш е н и е. Рассмотрим четыре гипотезы: Н₀ - в танк не попало ни одного снаряда. Н₁ - в танк попал один снаряд, Н 2 - в танк попало два снаряда и Н3 - в танк попало три снаряда.

Пользуясь теоремами сложения и умножения, найдем вероятности этих гипотез:

Р(Н0 )= 0,5*0,3*0,2=0,03;

Р(Н₁)=0,5*0,3*0,2+0,5*0,7*0,2+0,5*0,3*0,8=0,22; Р(Н₂)=0,5*0,7*0,2+0,5*0,3*0,8+0,5*0,7*0,8=0,47;

Р(Н3)=0,5*0,7*0,8=0,28.

Условные вероятности события А (выход из строя танка) при этих гипотезах равны:

Р(А/Н₀) = 0; Р(А/Н₁) = 0,3; Р(А/Н2) = 0,9; Р(А/Н3) = 1,0. Применяя формулу полной вероятности, получим

Р(А) = Р(Н0)*Р(А/Н0) + Р(Н₁)*Р(А/Н1) + Р(Н2)*Р(А/Н2) + Р(Н3)*Р(А/Н3)= =0,03*0+0,22.*0,3+0,47*0,9+0,28*1,0 = 0,769. В практике применения теории вероятностей часто приходится встречаться с задачами, в которых один и тот же опыт или аналогичные опыты повторяются многократно. В резуль­тате каждого опыта может появиться или не появиться некоторое событие А, причем нас ин­тересует не результат каждого отдельного опыта, а общее число появлений события А в ре­зультате серии опытов. Например, если производится группа выстрелов по одной и той же цели, то нас интересует не результат каждого выстрела, а общее число попаданий.

Если проводят n независимых опытов, в каждом из которых событие А появляется с вероятностью р, то вероятность того, что событие появится ровно т раз, выражается фор­мулой Бернулли

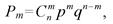
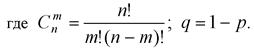(3.29)

Пример 3.12. При проведении стрельб из орудия по щиту было зафиксировано десять промахов (m = 10) из пятисот выстрелов (n = 500).

Определить вероятность того, что при ста выстрелах будет ровно четыре промаха, если считать, что все выстрелы независимы и вероятность промаха в каждом выстреле одинакова.

Р е ш е н и е. Найдем вероятность промаха при одном выстреле по формуле

Р = m/n = 10/500 = 0,002.

Далее по формуле (3.29) найдем вероятность появления четырех промахов из ста вы­стрелов ₄

Р4 = С = 0,002⁴ • 0,8^100-4 = 0,000003.

¹⁰⁰

Ответ: Р4 = 0,000003.

Дата добавления: 2014-12-26