Параметры средства Поиск решения

Таблица 5.1

Максимальное время	-служит для ограничения времени, отпущенного на поиск решения задачи. В этом поле можно ввести время в секундах, не превышающее 32 767 (примерно девять часов); значение 100, используемое по умолчанию, вполне приемлемо для решения большинства простых задач.
Предельное число итераций	-управляет временем решения задачи путем ограничения числа вычислительных циклов (итераций).
Относительная погрешность	- определяет точность вычислений. Чем меньше значение этого параметра, тем выше точность вычислений.
Допустимое отклонение	- предназначен для задания допуска на отклонение от оптимального решения, если множество значений влияющей ячейки ограничено множеством целых чисел. Чем больше значение допуска, тем меньше времени требуется на поиск решения.
Сходимость	- применяется только к нелинейным задачам. Когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в поле Сходимость, поиск прекращается.
Линейная модель	- служит для ускорения поиска решения путем применения к задаче оптимизации линейной модели. Нелинейные модели предполагают использование нелинейных функций, фактора роста и экспоненциального сглаживания, что замедляет вычисления.
Неотрицательные значения	- позволяет установить нулевую нижнюю границу для тех влияющих ячеек, для которых не было задано соответствующее ограничение в диалоговом окне Добавить ограничение.
Автоматическое масштабирование	- используется, когда числа в изменяемых ячейках и в целевой ячейке существенно различаются.
Показывать результаты итераций	- приостанавливает поиск решения для просмотра результатов отдельных итераций.
Загрузить модель	- после щелчка на этой кнопке отрывается одноименное диалоговое окно, в котором можно ввести ссылку на диапазон ячеек, содержащих модель оптимизации.
Сохранить модель	- служит для отображения на экране одноименного диалогового окна, в котором можно ввести ссылку на диапазон ячеек, предназначенный для хранения модели оптимизации.
Оценка линейная	- выберите этот переключатель для работы с линейной моделью.
Оценка квадратичная	- выберите этот переключатель для работы с нелинейной моделью.
Разности прямые	- используется в большинстве задач, где скорость изменения ограничений относительно невысока. Увеличивает скорость работы средства Поиск решения.
Разности центральные	- используется для функций, имеющих разрывную производную. Данный способ требует больше вычислений, однако его применение может быть оправданным, если выдано сообщение о том, что получить более точное решение не удается.
Метод поиска Ньютона	- требует больше памяти, но выполняет меньше итераций, чем в методе сопряженных градиентов.
Метод поиска сопряженных градиентов	- реализует метод сопряженных градиентов, для которого требуется меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно большая и необходимо экономить память или если итерации дают слишком малое отличие в последовательных приближениях.

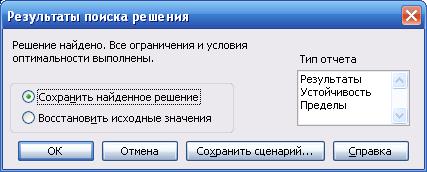
Задав все параметры, нажать кнопку Выполнить для поиска решения задачи. Если решение найдено, то появляется окно, с соответствующим сообщением (рис. 5.6).

	рис. 5.6

Результаты решения могут быть сохранены в файле задачи в виде сценарии или добавлены в виде отдельных листов Отчет по результатам, Отчет по устойчивости, Отчет по пределам. Для сохранения результатов в виде листов необходимо предварительно в поле Тип отчета выделить требуемые типы отчетов. В этом же окне можно отказаться от полученных решений и восстановить ис­ходные значения переменных.

Отчет по результатам приведен ниже на рис. 5.7. В данном отче­те в графах Результат выводятся значения целевой функции и оптимального плана, а также значения исходного опорного пла­на (графа Исходное значение). Кроме того, указывается, какие ограничения являются связанными, т.е. ограничения с дефи­цитным ресурсом (т.е его количество ограничивает план производства), а какие — нет (графа Статус), и приведены значения соответствующих дефицитов по всем ограничениям (графа Разница).

Отчеты по устойчивости и по пределам позволяют проанализировать модель на устойчивость. Устойчивость модели имеет важную роль на практике. Если значение оптимального решения резко изменяется при небольших отклонениях переменных, то такой моделью сложно пользоваться на практике, где изменения цен и запасов – явление обыденное. Возможности MS Excel анализировать модель на устойчивость в данном пособии не рассматриваются.

рис. 5.7

Тема 6. Транспортная задача.

Транспортные задачи, являясь подклассом задач линейного программирования, затрагивают, как правило, распределение ресурсов, находящихся у т производителей (поставщиков), по п потребителям этих ресурсов. К числу таких задач относятся:

— соответствие пунктов отправления и пунктов назначения;

— прикрепление потребителей ресурса к производителям;

— взаимная "привязка" грузопотоков прямого и обратного направлений;

— отдельные задачи оптимальной загрузки промышленного оборудования;

— оптимальное распределение объемов выпуска промышлен­ной продукции между заводами-изготовителями и др.

Рассмотрим модель транспортной задачи на примере прикреп­ления пунктов отправления к пунктам назначения.

В т пунктах отправления A₁, A₂,.,., А_т, которые в дальнейшем будем называть поставщиками, сосредоточено определенное коли­чество единиц некоторого однородного продукта, которое обозна­чим a_i (i = 1, 2,..., т). Данный продукт потребляется в п пунктах В₁, В₂,..., В_n, которые будем называть потребителями; объем потребле­ния обозначим b_j (j = 1, 2,..., п). Известны расходы на перевозку единицы продукта из пункта А_i в пункт B_j, которые равны с_ij и при­ведены в матрице транспортных расходов С = (с_ij).

Требуется составить такой план прикрепления потребителей к поставщикам, т.е. план перевозок, при котором весь продукт выво­зится из пунктов A_i в пункты B_j, в соответствии с потребностью и общая величина транспортных издержек будет минимальной.

Обозначим количество продукта, перевозимого из пункта A_i в пункт B_j через х_ij. Совокупность всех переменных х_ij- для краткости обозначим X, тогда целевая функция задачи будет иметь вид

(6.1)

А ограничения выглядят следующим образом:

(6.3)

(6.2)

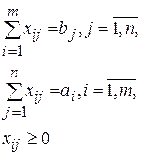
Условия (6.2) означают полное удовлетворение спроса во всех пунктах потребления; условия (6.3) определяют полный вывоз продукции от всех поставщиков.

Необходимым и достаточным условием разрешимости задачи (6.1)—(6.3) является условие баланса:

(6.4)

(6.5)

Транспортная задача, в которой имеет место равенство (6.4), называется закрытой иможет быть решена, как задача линейного программирования с помощью симплексного метода. Однако бла­годаря особенностям переменных задачи и систему ограничений разработаны специальные, менее громоздкие методы ее решения. Наиболее применяемым методом является метод потенциалов, при котором каждой i -й строке (i -му поставщику) устанавливается по­тенциал и_i,который можно интерпретировать как цену продукта в пункте поставщика, а каждому столбцу j (j-му потребителю) уста­навливается потенциал v_j, который можно принять условно за цену, продукта в пункте потребителя. В простейшем случае цена про­дукта в пункте потребителя равна его цене в пункте поставщика плюс транспортные расходы на его доставку, т.е.

v_j = u_i+с_ij

Пер­вым этапом алгоритма метода потенциалов является составление начального распределения (начального плана перевозок); для реализации этого на­чального этапа имеется в свою очередь рад методов: северо-за­падного угла, наименьших стоимостей, аппроксимаций Фогеля и др. Вторым этапом служат построение системы потенциалов на основе равенства (6.4) и проверка начального плана на оптимальность.

(6.6)

Чтобы оценить оптимальность распределения, для всех клеток (i, j) матрицы перевозок определяются их оценки, которые обозна­чим через , по формуле:

Используя ранее принятую интерпретацию, выражение (u_i+с_ij) можно трактовать как сумму цены продукта у поставщика и стоимо­сти перевозки; эта сумма путем вычитания сравнивается с ценой продукта у соответствующего потребителя v_j. Очевидно, оценки за­полненных клеток равны нулю (цена потребителя покрывает цену поставщика и стоимость перевозок). Таким образом, об оптимально­сти распределения можно судить по величинам оценок свободных клеток. Если оценка некоторой свободной клетки отрицательна, это можно интерпретировать так: цена, предлагаемая соответствующим потребителем, больше суммы цены поставщика и стоимости пере­возки, т.е. если бы эта клетка была занята, то можно было бы полу­чить дополнительный экономический эффект. Следовательно, усло­вием оптимальности распределения служит условие неотрицательности оценок свободных клеток матрицы перевозок.

В случае его неоптимальности переходят к третьему этапу, содержа­ние которого заключается в реализации так называемых циклов пе­рераспределения (корректировка плана прикрепления потребителей к поставщикам), после чего переходят опять ко второму этапу. Сово­купность процедур третьего и второго этапов образует одну итера­цию; эти итерации повторяются, пока план перевозок не окажется оптимальным по критерию (6.1).

Рассмотрим этапы реализации метода потенциалов для закры­той транспортной задачи более подробно. Прежде всего следует от­метить, что при условии баланса (6.4) ранг системы линейных уравнений (6.2), (6.3) равен т+п— 1; таким образом из общего числа т п неизвестных базисных неизвестных будет т+п— 1. Вследствие этого при любом допустимом базисном распределении в матрице перевозок (таблице поставок), будет занято ровно т + п— 1 клеток, которые бу­дем называть базисными в отличие от остальных, свободных, клеток; занятые клетки будем отмечать диагональной чертой.

Таблица 6.1

Продукт	Объем потребления
b1	b2	…	bn
a1	c11 x11	c12 x12	…	c1n x1n
a2	c21 x21	c22 x22	…	c2n x2n
…	…	…	…	…
am	cm1 xm1	cm2 xm2	…	cmn xmn

Если баланс (6.4) не выполняется, то ограничения (6.2) или (6.3) имеют вид неравенств типа «меньше или равно»; транспорт­ная задача в таком случае называется открытой. Для решения от­крытой транспортной задачи методом потенциалов ее сводят к за­крытой задаче путем ввода или фиктивного потребителя, если в неравенства превращаются условия (6.2), или фиктивного поставщика — в случае превращения в неравенства ограничений (6.2).

Пример 11. Торговая фирма "Солнце и Луна" включает четыре пред­приятия и шесть складов в различных регионах страны. Каждый месяц предприятия фирмы производят 60, 100 и 120 ед. про­дукции. Вся производимая продукция направляется на склады, вместимость которых следующая: 30, 100, 40 и 110 ед. про­дукции. Издержки транспортировки продукции от предприятий до складов следующие (ден. ед.):

Таблица 6.2

Предприятия фирмы "Солнце и Луна"	Склады

Распределите план перевозок из условия минимизации еже­месячных расходов на транспортировку.

Решение: Условие баланса (6.4) соблюдается поэтому нет необходимости вводит фиктивного потребителя или поставщика.

Этап 1. Первоначальное закрепление потребителей за поставщи­ками. Рассмотрим два метода получения начального распределения (начального опорного плана): метод северо-западного угла и метод наименьших стоимостей. При каждом из этих методов при заполне­нии некоторой клетки, кроме последней, вычеркивается или только строка матрицы перевозок, или только столбец; лишь при заполнении последней клетки вычеркиваются и строка, и столбец. Такой подход будет гарантировать, что базисных клеток будет ровно т + п— 1. Ес­ли при заполнении некоторой (не последней) клетки одновременно удовлетворяются мощности и поставщика, и потребителя, то вычер­кивается, например, только строка, а в соответствующем столбце заполняется незанятая клетка так называемой «нулевой поставкой», после чего вычеркивается и столбец. Для идентификации клетки обычно в скобках указываются номера ее строки и столбца.

В методе северо-западного угла всегда в первую очередь запол­няется клетка (из числа невычеркнутых), стоящая в верхнем левом (северо-западном) углу матрицы перевозок. Пример составления начального распределения данным методом показан в табл. 6.3: за­полняется клетка (1;1) и вычеркивается первый столбец; заполняется клетка (1;2) и вычеркивается первая строка; заполняется клетка (2;2) и вычеркивается второй столбец; заполняется клетка (2;3) и вычеркивается вторая строка; заполняется клетка (3;3) и вы­черкивается третий столбец; наконец, заполняется клетка (3,4) и вычеркиваются последние строка и столбец. Число занятых клеток равно т + п —1 = 3 + 4— 1 = 6. Суммарные затраты на реализацию данного плана

f( 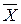)=4 ·30+5·30+3·70+6·30+7·10+4·110=1170

В примерах далее заполненные клетки будем закрашивать, а не выделять диагональной чертой.

Таблица 6.3

Поставщики	Потребители

Недостатком данного метода является то, что он не учитывает зна­чения элементов c_ij матрицы транспортных расходов, в результате чего полученное этим методом начальное распределение (начальный опор­ный план перевозок) может быть достаточно далеко от оптимального.

В различных модификациях метода наименьших стоимостей запол­нение клеток матрицы перевозок проводится с учетом значений вели­чин c_ij. Так, в модификации «двойного предпочтения» отмечают клетки с наименьшими стоимостями перевозок сначала по каждой строке, а затем по каждому столбцу. Клетки, имеющие две отметки, заполняют в первую очередь, затем заполняют клетки с одной отметкой, а данные о нераспределенном грузе записывают в неотмеченные клетки с наи­меньшими стоимостями. При этом из двух клеток с одинаковой стои­мостью перевозок предпочтение отдается клетке, через которую осу­ществляется больший объем перевозок. Вычеркивание строк и столб­цов при заполнении клеток проводится по описанным выше прави­лам.

Пример начального распределения методом наименьших стоимо­стей представлен в табл. 6.4.

f( 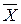)=1 ·30+2·100+2·40+3·20+2·70+4·20=590

Следовательно, данный план перевозок значительно ближе к оп­тимальному, чем план, составленный по методу северо-западного угла.

Таблица 6.4

Поставщики	Потребители
			2 vv
	1 vv			2 v
		2 vv

Этап 2. Проверка оптимальности полученного плана перевозок.

Введем специальные показатели и_i, для каждой строки матрицы пе­ревозок (каждого поставщика), где i = 1, 2,..., m, и показатели v_j для каж­дого столбца (каждого потребителя), где j = 1, 2,..., n. Эти показатели называются потенциалами поставщиков и потребителей, их удобно интерпретировать как цены продукта в соответствующих пунктах поставщиков и потребителей. Потенциалы подбираются таким об­разом, чтобы для заполненной клетки (i; j) выполнялось равенство (6.5). Совокупность уравнений вида (6.5), составленных для всех заполненных клеток (всех базисных неизвестных), образует систему т + п — 1 линейных уравнений с т + п неизвестными и_i и v_j. Эта система всегда совместна, причем значение одного из неизвестных можно задавать произвольно (например, и₁ = 0), тогда значения остальных неизвестных находятся из системы однозначно.

Рассмотрим процесс нахождения потенциалов для базисного начального распределения по методу северо-западного угла, пред­ставленного в табл. 6.3. Задав и₁ = 0 и используя формулу (6.5) для заполненных клеток (1;1) и (1;2), находим v₁ = 4 и v₂ =5. Зная, v₂ по заполненной клетке (2;2) находим и₂ = 2, а зная и₂ , по заполненной клетке (2;3) находим v₃ = 8. Зная v₃ по заполненной клетке (3;3) находим и₃ = 1, а затем по заполненной клетке (3;4) находим v₄ = 5. Результаты представлены в табл. 6.5, где потен­циалы поставщиков приведены в последнем столбце, а потенциа­лы потребителей — в последней строке.

Таблица 6.5

Поставщики	Потребители	иi
		5 - 30	2 +
		3 +	6 -
vj

Смысл прямоугольного контура, проведенного пунктиром в табл. 6.5, и знаков при его вершинах пояснен далее при описании этапа 3 метода потенциалов.

Чтобы оценить оптимальность распределения, для всех клеток (i, j) матрицы перевозок определяются их оценки, которые обозна­чим через , по формуле (6.6). Оценки клеток удобно представить в виде матрицы оценок. Дляранее рассматриваемого распределения, полу­ченного методом северо-западного угла (см. табл. 6.3), матрица оценок клеток имеет вид:

(6.7)

Таким образом, об оптимально­сти распределения можно судить по величинам оценок свободных клеток. Если оценка некоторой свободной клетки отрицательна, это можно интерпретировать так: цена, предлагаемая соответствующим потребителем, больше суммы цены поставщика и стоимости пере­возки, т.е. если бы эта клетка была занята, то можно было бы полу­чить дополнительный экономический эффект. Следовательно, усло­вием оптимальности распределения служит условие неотрицательности оценок свободных клеток матрицы перевозок.

Этап 3. Улучшение неоптимального плана перевозок (циклы пере­распределения). Чтобы улучшить неоптимальный план перевозок, вы­бирается клетка матрицы перевозок с отрицательной оценкой; если таких клеток несколько, то обычно (но необязательно) выбирается клетка с наибольшей по абсолютной величине отрицательной оцен­кой. Например, для распределения, представленного в табл. 6.5, такой клеткой может служить клетка (1;3) (см. матрицу оценок (6.7)).

Для выбранной клетки строится замкнутая линия (контур), на­чальная вершина которой лежит в выбранной клетке, а все осталь­ные вершины находятся в занятых клетках; при этом направления отдельных отрезков контура могут быть только горизонтальными и вертикальными. Вершиной контура, кроме первой, является заня­тая клетка, где отрезки контура образуют один прямой угол (нельзя рассматривать как вершины клетки, где горизонтальные и верти­кальные отрезки контура пересекаются). Очевидно, число отрезков контура, как и его вершин, будет четным. В вершинах контура расставляются поочередно знаки «+» и «-», начиная со знака «+» в выбранной свободной клетке. Пример простого контура показан пунктиром табл. 3.8, хотя вид контура может быть самым разно­образным (см. рис. 6.1).

рис. 6.1

Величина перераспределяемой поставки определяется как наи­меньшая из величин поставок в вершинах контура со знаком «-» и на эту величину увеличиваются поставки в вершинах со знаком «+» и уменьшаются поставки в вершинах со знаком «-». Это правило гарантирует, что в вершинах контура не появится отрицательных по­ставок, начальная выбранная клетка окажется занятой, в то время как одна из занятых клеток при этом обязательно освободится. Если величина перераспределяемой поставки равна поставкам не в одной, а в нескольких вершинах контура со знаком «-» (это как раз имеет место в контуре перераспределения в табл. 6.5), то освобождается только одна клетка, обычно с наибольшей стоимостью перевозки, а все другие такие клетки остаются занятыми с нулевой поставкой.

Результат указанных операций для представленного в табл. 6.5 распределения поставок показан в табл. 6.6. Суммарные затраты на перевозки по этому плану составляют:

f( 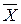)= 4·30+5·0+2·30+3·100+7·10+4·110=990

что меньше предыдущей суммы затрат.

Таблица 6.6

Поставщики	Потребители	иi
					-1
					-3
vj

Рассчитаем потенциалы строк и столбцов и оценки:

Транспортные задачи, в базисном плане перевозок которых имеют место занятые клетки с нулевой поставкой (или в первоначальном распределении, или в процессе итераций), называются вырожденными.

Пример такой задачи представлен в табл. 6.6. В случае вырож­денной транспортной задачи существует опасность зацикливания, т.е. бесконечного повторения итераций (бесконечного перебора одних и тех же базисных комбинаций занятых клеток). Как правило, в прак­тических задачах транспортного типа зацикливание не встречается; тем не менее следует знать, что существуют специальные правила, позволяющие выйти из цикла, если зацикливание все же произойдет.

Следует соответствующие нулевые элементы опорного плана заменить сколь угодно малым положительным числом и решать задачу как невырожденную. В оптимальном плане такой задачи необходимо считать равным нулю.

При отсутствии вырождения метод потенциалов конечен и приводит к оптимальному плану перевозок за конечное число шагов.

Дата добавления: 2014-12-26