Тесты для связанных выборок (related samples) 2 страница

Почему не 4 индексные переменные? Четвертая переменная определяется однозначно через первые три, поэтому, введение ее вызвало бы коллинеарность, не позволяющую найти коэффициенты регрессии.

Вот задание, которое позволяет изучить зависимость душевого дохода от возраста и семейного положения:

compute lnv14m =ln(v14/200).

compute t1=(v11=1).

compute t2=(v11=2).

compute t3=(v11=3).

Compute v9_2=v9**2.

*квадрат возраста.

REGRESSION /DEPENDENT lnv14m /METHOD=ENTER v9 v9_2 t1 t2 t3 /SAVE PRED.

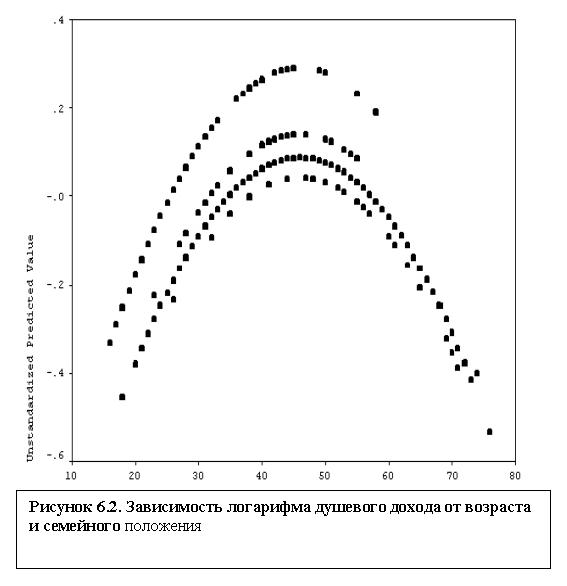
График связи возраста (V9) с предсказанным уравнением логарифмом доходов (переменная pre_2) получается командой

GRAPH /SCATTERPLOT(BIVAR)=v9 WITH pre_2 /MISSING=LISTWISE

Он представляет собой 4 параболы (рисунок 6.2). В соответствии с коэффициентами перед t1, t2 и t3 (см. таблицу 6.4), эти пораболы соответствуют, сверху вниз, холостякам, разведенным, женатым и вдовцам (порабола холостяков получается при t1=t2 = t3=0).

Вероятно, полученное уравнение можно улучшить, исключив из уравнения переменные с незначимыми коэффициентами. Поскольку индексные переменные должны быть в определенной степени взаимосвязаны, уровень наблюдаемой значимости может определяться здесь коллинеарностью, поэтому "ревизию" переменных нужно проводить осторожно, чтобы существенно не ухудшить полученного уравнения.

Из-за взаимосвязи переменных здесь нет возможности говорить о том, какая переменная больше влияет на зависимую переменную. Обратите внимание на довольно редкий эффект: бета-коэффициенты для возраста и его квадрата по абсолютной величине больше 1!

Таблица 6.4. Коэффициенты регрессии с индексными переменными.

	B	Std. Error	Beta	T	Sig.
(Constant)	-1.1721	0.1937		-6.0500	0.0000
V9 Возраст	0.0635	0.0105	1.4298	6.0299	0.0000
V9_2	-0.0007	0.0001	-1.3243	-5.7351	0.0000
T1 Женат	-0.2030	0.0766	-0.1540	-2.6488	0.0083
T2 Вдовец	-0.2471	0.1352	-0.0850	-1.8279	0.0680
T3 Разведен	-0.1494	0.1134	-0.0661	-1.3176	0.1881

Кроме того, модель с тремя "параллельными" параболами, вероятно, не полностью адекватна, каждая группа может иметь свою конфигурацию линии регрессии. Для учета этого в уравнении стоит использовать переменные взаимодействия. О том, как их конструировать - следующий раздел.

Взаимодействие переменных

Предположим, что мы рассматриваем пару индикаторных переменных: X¹ - для выделения группы женатых и X² - для выделения группы "начальников", а прогнозируем с помощью уравнения регрессии все тот же логарифм дохода: Y=B₀+B₁*X¹+B₂*X².

Это уравнение моделирует ситуацию, когда действие факторов X¹ и X² складывается, т.е. считается, к примеру, что женатый начальних имеет зарплату B₁+B₂, не женатый начальник B₂. Это достаточно смелое предположение, так как, скорее всего, закономерность не так груба и существует взаимодействие между факторами, в результате которого их совместный вклад имеет другую величину. Для учета такого взаимодействия можно ввести в уравнение переменную, равную произведению X¹ и X²:

Y=B₀+B₁*X¹+B₂*X²+B₃*X¹*X².

Произведение X¹*X² равно единице, если факторы действуют совместно и нулю, если какой либо из факторов отсутствует.

Аналогично можно поступить для учета взаимодействия обычных количественных переменных, а также индексных переменных с количественными.

Для получения переменных взаимодействия, следует воспользоваться средствами преобразования данных SPSS.

6.2. Логистическая регрессия

Предсказания событий, исследования связи событий с теми или иными факторами с нетерпением ждут от социологов. Будем считать, что событие в данных фиксируется дихотомической переменной (0 не произошло событие, 1 - произошло). Для построения модели предсказания можно было бы построить, к примеру, линейное регрессионное уравнение с зависимой дихотомической переменной Y, но оно будет не адекватно поставленной задаче, так как в классическом уравнении регрессии предполагается, что Y - непрерывная переменная. С этой целью рассматривается логистическая регрессия. Ее целью является построение модели прогноза вероятности события { Y =1} в зависимости от независимых переменных X¹,…,X^p. Иначе эта связь может быть выражена в виде зависимости P{Y=1|X}=f(X)

Логистическая регрессия выражает эту связь в виде формулы

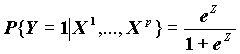, где Z=B₀+B₁X¹+…+B_pX^p (1).

Название "логистическая регрессия" происходит от названия логистического распределения, имеющего функцию распределения 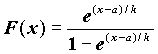. Таким образом, модель, представленная этим видом регрессии, по сути, является функцией распределения этого закона, в которой в качестве аргумента используется линейная комбинация независимых переменных.

Отношение шансов и логит

Отношение вероятности того, что событие произойдет к вероятности того, что оно не произойдет P/(1-P) называется отношением шансов.

С этим отношением связано еще одно представление логистической регрессии, получаемое за счет непосредственного задания зависимой переменной в виде Z=Ln(P/(1-P)), где P=P{Y=1|X¹,…,X^p}. Переменная Z называется логитом. По сути дела, логистическая регрессия определяется уравнением регрессии Z=B₀+B₁X¹+…+B_pX^p.

В связи с этим отношение шансов может быть записано в следующем виде

P/(1-P)= .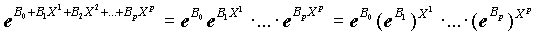

Отсюда получается, что, если модель верна, при независимых X¹,…,X^p изменение X^k на единицу вызывает изменение отношения шансов в 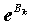раз.

Решение уравнения с использованием логита.

Механизм решения такого уравнения можно представить следующим образом

1. Получаются агрегированные данные по переменным X, в которых для каждой группы, характеризуемой значениями X_j= 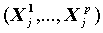подсчитывается доля объектов, соответствующих событию {Y=1}. Эта доля является оценкой вероятности 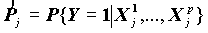. В соответствии с этим, для каждой группы получается значение логита Z_j.
2. На агрегированных данных оцениваются коэффициенты уравнения Z=B₀+B₁X¹+…+B_pX^p. К сожалению, дисперсия Z здесь зависит от значений X, поэтому при использовании логита применяется специальная техника оценки коэффициентов - взвешенной регрессии.

Еще одна особенность состоит в том, что в реальных данных очень часто группы по X оказываются однородными по Y, поэтому оценки 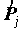оказываются равными нулю или единице. Таким образом, оценка логита для них не определена (для этих значений ).

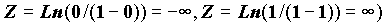В некоторых статистических пакетах такие группы объектов просто-напросто отбрасываются.

В настоящее время в статистическом пакете для оценки коэффициентов используется метод максимального правдоподобия, лишенный этого недостатка. Тем не менее, проблема, хотя и не в таком остром виде остается: если оценки вероятности для многих групп оказываются равными нулю или единице, оценки коэффициентов регрессии имеют слишком большую дисперсию. Поэтому, имея в качестве независимых переменных такие признаки, как душевой доход в сочетании с возрастом, их следует укрупнить по интервалам, приписав объектам средние значения интервалов.

Неколичественные данные

Если в обычной линейной регрессии для работы с неколичественными переменными нам приходилось подготавливать специальные индикаторные переменные, то в реализации логистической регрессии в SPSS это делается автоматически. Для этого в диалоговом окне специально предусмотрены средства, сообщающие пакету, что ту или иную переменную следует считать категориальной. При этом, чтобы не получить линейно зависимых переменных, максимальный код ее значения (или минимальный, в зависимости от задания процедуры) не перекодируется в дихотомическую (индексную) переменную. Впрочем, средства преобразования данных позволяют не учитывать любой код значения. Имеются другие способы перекодирования категориальных (неколичественных) переменных в несколько переменных, но мы будем пользоваться только указанным, как наиболее естественным.

Взаимодействие переменных

В процедуре логистической регрессии в SPSS предусмотрены средства для автоматического включения в уравнение переменных взаимодействий. В диалоговом окне в списке исходных переменных для этого следует выделить имена переменных, взаимодействия которых предполагается рассмотреть, затем переправить выделенные имена в окно независимых переменных кнопкой c текстом > a *b>.

Пример логистической регрессии и статистики

Процедура логистической регрессии в SPSS в диалоговом режиме вызывается из меню командой Statistics\Regression\Binary logistic….

В качестве примера по данным RLMS изучим, как связано употребление спиртных напитков с зарплатой, полом, статусом (ранг руководителя), курит ли он.

Для этого подготовим данные: выберем в обследовании RLMS население старше 18 лет, сконструируем индикаторы курения (smoke) и пития (alcohol) (в обследовании задавался вопрос "Употребляли ли Вы в течении 30 дней алкогольные напитки")

COMPUTE filter_$=(vozr>18).

FILTER BY filter_$.

compute smoke=(dm71=1).

val lab smoke 1 "курит" 0 "не курит".

compute alcohol=(dm80=1).

val lab alcohol 1 "пьет" 0 "не пьет".

Укрупним переменную dj10 -(зарплата на основном рабочем месте). В данном случае группы по значениям этой переменной в основном достаточно наполнены, но мы с методической целью покажем один из способов укрупнения. Для этого вначале получаем переменную wage, которая содержит номера децилей по зарплате, затем среднюю зарплату по этим децилям (см. таблицу 6.5).

missing values dj6.0 (9997,9998,9999) dj10(99997,99998,99999).

RANK VARIABLES=dj10 (A) /NTILES (10) into wage /PRINT=YES /TIES=MEAN.

MEANS TABLES=dj10 BY wage /CELLS MEAN.

Таблица 6.5. Средняя зарплата по децилям.

WAGE децили зарплаты
DJ10 зарплата за 30 дней

Полученные средние используем для формирования переменной, соответствующей укрупненной зарплате (для удобства, чтобы коэффициенты регрессии не были слишком малы, в качестве единицы ее измерения возьмем сто рублей).

recode wage (1=1.01) (2=2.11) (3=3.07) (4=4.16) (5=5.42) (6=7.03) (7=8.53) (8=11.08) (9=15.65) (10 =34.64).

recode dj6.0 (sysmis=4)(1 thru 5=1)(6 thru 10=2) (10 thru hi=3) into manag.

var lab manag "статус" wage "зaработок".

val lab manag 4 "не начальник" 1 "шеф" 2 "начальничек" 3 "начальник".

exec.

Далее формируем переменную manag - " статус" из переменной dj6.0 - количество подчиненных.

Запускаем команду построения регрессии LOGISTIC REGRESSION, в которой использованы переменные wage - зарплата, manag статус, dh5 - пол (1 мужчины, 2 женщины) smoke - курение (1 курит, 0 не курит), dh5* wage - "взаимодействие" пола с зарплатой (для женщин значение - 0, для мужчин - совпадает с зарплатой).

LOGISTIC REGRESSION VAR=alcohol /METHOD=ENTER wage manag dh5 smoke dh5*wage /CONTRAST (dh5)=Indicator /CONTRAST (manag)=Indicator /CONTRAST (smoke)=Indicator /PRINT=CI(95) /CRITERIA PIN(.05) POUT(.10) ITERATE(20) CUT(.69).

В выдаче программа, прежде всего, сообщает о перекодировании данных:

Dependent Variable Encoding:

Original Internal

Value Value

.00 0

1.00 1

Следует обратить внимание, что зависимая переменная здесь должна быть дихотомической, и ее максимальный код считается кодом события, вероятность которого прогнозируется. Например, если Вы закодировали переменную ALCOHOL 1-употреблял, 2-не употреблял, то будет прогнозироваться вероятность не употребления алкоголя.

Далее идут сведения о кодировании индексных переменных для категориальных переменных; из-за их естественности мы их здесь не приводим.

Далее следуют обозначения для переменных взаимодействия, в нашем простом случае это:

Interactions:

INT_1 DH5(1) by WAGE

Качество подгонки логистической регрессии

Далее в выдаче появляется описательная информация о качестве подгонки модели:

-2 Log Likelihood 3289.971

Goodness of Fit 2830.214

Cox & Snell - R^2.072

Nagelkerke - R^2.102

которые означают:

• -2 Log Likelihood - удвоенный логарифм функция правдоподобия со знаком минус;
• Goodness of Fit - характеристика отличия наблюдаемых частот от ожидаемых;
• Cox & Snell - R^2 и Nagelkerke - R^2 - псевдо коэффициенты детерминации, полученные на основе отношения функций правдоподобия моделей лишь с константой и со всеми коэффициентами.

Эти коэффициенты стоит использовать при сравнении очень похожих моделей на аналогичных данных, что практически нереально, поэтому мы не будем на них останавливаться.

Вероятность правильного предсказания

На основе модели логистической регрессии можно строить предсказание произойдет или не произойдет событие {Y=1}. Правило предсказания, по умолчанию заложенное в процедуру LOGISTIC REGRESSION устроено по следующему принципу: если 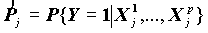>0.5 считаем, что событие произойдет; 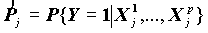£ 0.5, считаем, что событие не произойдет. Это правило оптимально с точки зрения минимизации числа ошибок, но очень грубо с точки зрения исследования связи. Зачастую оказывается, что вероятность события P{Y=1} мала (значительно меньше 0.5) или велика (значительно больше 0.5), поэтому оказывается, что все имеющиеся в данных сочетания X предсказывают событие или все предсказывают противоположное событие.

Поэтому здесь необходима другая классификация, которая демонстрирует связь между зависимой и независимыми переменными. С этой целью стоит отнести к предсказываемому классу 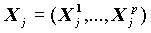, для которых {Y=1} ожидается c большей вероятностью, чем в среднем, а остальные - к противоположному классу. В нашем случае доля употреблявших алкоголь равна 69% и мы к классу предсказанных значений отнесли значения X, для которых 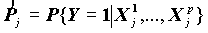>0.69. Поэтому в процедуре указан параметр /CRITERIA CUT(.69). Связь между этими классификациями представлена таблица сопряженности (рмсунок 6.3). Но лучше в этой таблице вычислить процентные соотношения пользуясь EXCEL или калькулятором.

Таблица 6.6. Связь наблюдения и предсказания в логистической регрессии

Наблюдается	Предсказано
Не пьет	Пьет	Всего
Не пьет	43.8%	21.5%	31.3%
Пьет	56.2%	78.5%	68.7%

Коэффициенты регрессии

Основная информация содержится в таблице коэффициентов регрессии (рисунок 6.4). Прежде всего, следует обратить внимание на значимость коэффициентов. Наблюдаемая значимость вычисляется на основе статистики Вальда. Эта статистика связана с методом максимального правдоподобия и может быть использована при оценках разнообразных параметров.

Универсальность статистики Вальда позволяет оценить значимость не только отдельных переменных, но и в целом значимость категориальных переменных, несмотря на то, что они дезагрегированы на индексные переменные. Статистика Вальда имеет распределение хи-квадрат. Число степеней свободы, равно единице, если проверяется гипотеза о равенстве нулю коэффициента при обычной или индексной переменной и, для категориальной переменной, равно числу значений без единицы (числу соответствующих индексных переменных). Квадратный корень из статистики Вальда приближенно равен отношению величины коэффициента к его стандартной ошибке - так же выражается t-статистика в обычной линейной модели регрессии.

В нашей таблице коэффициентов почти все переменные значимы на уровне значимости 5%. Закрыв глаза на возможное взаимодействие между независимыми переменными (коллинеарность), можно считать, что вероятность употребления алкоголя повышена при высокой зарплате, а также, у руководителей различного ранга. Из-за незначимости статистики Вальда нет, правда, полной уверенности относительно повышенной вероятности для начальников, имеющих более 10 подчиненных. Курение и принадлежность к мужскому полу также повышают эту вероятность, однако, взаимодействие "мужчина-зарплата" имеет обратное действие.

В этой же таблице присутствует аналог коэффициента корреляции (R), также построенный на основе статистики Вальда. Для обычных и индексных переменных положительные значения коэффициента свидетельствуют о положительной связи переменной с вероятностью события, отрицательные - об отрицательной связи.

Кроме того, мы выдали таблицу экспонент коэффициентов e^B и их доверительные границы (см. рисунок 6.5). Эта таблица выдана подкомандой /PRINT=CI(95) в команде задания логистической регрессии.

Согласно модели и полученным значениям коэффициентов, при фиксированных прочих переменных, принадлежность к мужскому полу увеличивает отношение шансов "пития" и "не пития" в 2.4 раза (точнее в 1.84-3.15 раза), курения - в 1.9 раза (1.54 - 2.35), а прибавка к зарплате 100 рублей - на 4.4% (2.8%-6%), правда такая прибавка мужчине одновременно уменьшает это отношение на 3.8% (5.7%-1.9%). Быть мелким начальником - значит увеличить отношение шансов в 1.43 (1.06 - 1.9) раза, чем в среднем, а средним начальником - в 1.7 (1.07-2.67) раза.

О статистике Вальда

Как отмечено в документации SPSS, недостаток статистики Вальда в том, что при малом числе наблюдений она может давать заниженные оценки наблюдаемой значимости коэффициентов. Для получения более точной информации о значимости переменных можно воспользоваться пошаговой регрессией, метод FORWARD LR (LR - likelihood ratio - отношение правдоподобия), тогда будет для каждой переменной выдана значимость включения/исключения, полученная на основе отношения функций правдоподобия модели. Поскольку основная выдача построена на основе статистики Вальда, первые выводы удобнее делать на ее основе, а потом уже уточнять результаты, если это необходимо.

Сохранение переменных

Программа позволяется сохранить множество переменных, среди которых наиболее полезной является, вероятно, предсказанная вероятность.

7. Исследование структуры данных

Конечно, собирая данные, исследователь руководствуется определенными гипотезами, информация относятся к избранным предмету и теме исследования, но нередко она представляет собой сырой материал, в котором нужно изучить структуру показателей, характеризующих объекты, а также выявить однородные группы объектов. Полезно представить эту информацию в геометрическом пространстве, лаконично отразить ее особенности в классификации объектов и переменных. Такая работа создает предпосылки к созданию типологий объектов и формулированию "социального пространства", в котором обозначены расстояния между объектами наблюдения, позволяет наглядно представить свойства объектов.

7.1. Факторный анализ

Идея метода состоит в сжатии матрицы признаков в матрицу с меньшим числом переменных, сохраняющую почти ту же самую информацию, что и исходная матрица. В основе моделей факторного анализа лежит гипотеза, что наблюдаемые переменные являются косвенными проявлениями небольшого числа скрытых (латентных) факторов. Хотя такую идею можно приписать многим методам анализа данных, обычно под моделью факторного анализа понимают представление исходных переменных в виде линейной комбинации факторов.

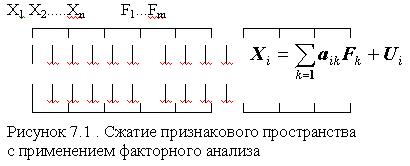
Факторы F построены так, чтобы наилучшим способом (с минимальной погрешностью) представить Х. В этой модели "скрытые" переменные F_k называются общими факторами, а переменные U_i специфическими факторами ("специфический" -это лишь один из переводов применяемого в англоязычной литературе слова Unique, в отечественной литературе в качестве определения U_i встречаются также слова "характерный", "уникальный"). Значения a_ik называются факторными нагрузками.

Обычно (хотя и не всегда) предполагается, что X_i стандартизованы (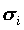 =1, X_i=0), а факторы F₁,F₂,…,F_m независимы и не связаны со специфическими факторами U_i (хотя существуют модели, выполненные в других предположениях). Предполагается также, что факторы F_i стандартизованы.

В этих условиях факторные нагрузки a_ik совпадают с коэффициентами корреляции между общими факторами и переменными X_i. Дисперсия X_i раскладывается на сумму квадратов факторных нагрузок и дисперсию специфического фактора:

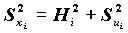, где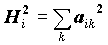

Величина 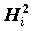называется общностью, 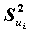- специфичностью. Другими словами, общность представляет собой часть дисперсии переменных, объясненную факторами, специфичность - часть не объясненной факторами дисперсии.

В соответствии с постановкой задачи, необходимо искать такие факторы, при которых суммарная общность максимальна, а специфичность - минимальна.

метод главных компанент

Один из наиболее распространенных методов поиска факторов, метод главных компонент, состоит в последовательном поиске факторов. Вначале ищется первый фактор, который объясняет наибольшую часть дисперсии, затем независимый от него второй фактор, объясняющий наибольшую часть оставшейся дисперсии, и т.д. Описание всей математики построения факторов слишком сложно, поэтому для пояснения сути мы прибегнем к зрительным образам (рисунок 7.2).

Геометрически это выглядит следующим образом. Для построения первого фактора берется прямая, проходящая через центр координат и облако рассеяния данных. Объектам можно сопоставить расстояния их проекций на эту прямую до центра координат, причем для одной из половин прямой (по отношению к нулевой точке) можно взять эти расстояния с отрицательным знаком. Такое построение представляют собой новую переменную, которую мы просто назовем осью. При построении фактора отыскивается такая ось, чтобы ее дисперсия была максимальна. Это означает, что этой осью объясняется максимум дисперсии переменных. Найденная ось после нормировки используется в качестве первого фактора. Если облако данных вытянуто в виде эллипсоида (имеет форму "огурца"), фактор совпадет с направлением, в котором вытянуты объекты, и по нему (по проекциям) с наибольшей точностью можно предсказать значения исходных переменных.

Для поиска второго фактора ищется ось, перпендикулярная первому фактору, также объясняющая наибольшую часть дисперсии, не объясненной первой осью. После нормировки эта ось становится вторым фактором. Если данные представляют собой плоский элипсоид ("блин") в трехмерном пространстве, два первых фактора позволяют в точности описать эти данные.

Максимально возможное число главных компонент равно количеству переменных. Сколько главных компонент необходимо построить для оптимального представления рассматриваемых исходных факторов?

Обозначим l _k объясненную главной компонентой F_k часть суммарной дисперсии совокупности исходных факторов. По умолчанию, в пакете предусмотрено продолжать строить факторы, пока l _к >1. Напомним, что переменные стандартизованы, и поэтому нет смысла строить очередной фактор, если он объясняет часть дисперсии, меньшую, чем приходящуюся непосредственно на одну переменную. При этом следует учесть, что l ₁>l ₂>l _3,….

К сведению читателя заметим, что значения l _k являются также собственными значениями корреляционной матрицы X_i, поэтому в выдаче они будут помечены текстом "EIGEN VALUE", что в переводе означает "собственные значения".

Заметим, что техника построения главных компонент расходится с теоретическими предположениями о факторах: имеется m+n независимых факторов, полученных методом главных компонент в n -мерном пространстве, что невозможно.

Интерпретация факторов.

Как же можно понять, что скрыто в найденных факторах? Основной информацией, которую использует исследователь, являются факторные нагрузки. Для интерпретации необходимо приписать фактору термин. Этот термин появляется на основе анализа корреляций фактора с исходными переменными. Например, при анализе успеваемости школьников фактор имеет высокую положительную корреляцию с оценкой по алгебре, геометрии и большую отрицательную корреляцию с оценками по рисованию - он характеризует точное мышление.

Не всегда такая интерпретация возможна. Для повышения интерпретируемости факторов добиваются большей контрастности матрицы факторных нагрузок. Метод такого улучшения результата называется методом ВРАЩЕНИЯ ФАКТOРОВ. Его суть состоит в следующем. Если мы будем вращать координатные оси, образуемые факторами, мы не потеряем в точности представления данных через новые оси, и не беда, что при этом факторы не будут упорядочены по величине объясненной ими дисперсии, зато у нас появляется возможность получить более контрастные факторные нагрузки. Вращение состоит в получении новых факторов - в виде специального вида линейной комбинации имеющихся факторов:

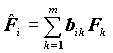
Чтобы не вводить новые обозначения, факторы и факторные нагрузки, полученные вращением, будем обозначать теми же символами, что и до вращения. Для достижения цели интерпретируемости существует достаточно много методов, которые состоят в оптимизации подходящей функции от факторных нагрузок. Мы рассмотрим реализуемый пакетом метод VARIMAX. Этот метод состоит в максимизации "дисперсии" квадратов факторных нагрузок для переменных:

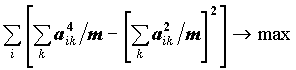
Чем сильнее разойдутся квадраты факторных нагрузок к концам отрезка [0,1], тем больше будет значение целевой функции вращения, тем четче интерпретация факторов.

Оценка факторов

Математический аппарат, используемый в факторном анализе, в действительности позволяет не вычислять непосредственно главные оси. И факторные нагрузки до и после вращения факторов и общности вычисляются за счет операций с корреляционной матрицей. Поэтому оценка значений факторов для объектов является одной из проблем факторного анализа.

Факторы, имеющие свойства полученных с помощью метода главных компонент, определяются на основе регрессионного уравнения. Известно, что для оценки регрессионных коэффициентов для стандартизованных переменных достаточно знать корреляционную матрицу переменных. Корреляционная матрица по переменным X_i и F_k определяется, исходя из модели и имеющейся матрицы корреляций X_i. Исходя из нее, регрессионным методом находятся факторы в виде линейных комбинаций исходных переменных: .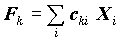

Дата добавления: 2014-12-27