
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема 29.2. Пусть дифференцируема на и для всех выполняется неравенство . Тогда возрастает на
Теорема 29.1. Пусть функция дифференцируема на интервале. Она не убывает (не возрастает) на тогда и только тогда, когда для всех выполняется неравенство.
◄Пусть 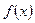 не убывает на
не убывает на 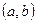 (случай невозрастания рассматривается аналогично). Тогда рассмотрим произвольную точку
(случай невозрастания рассматривается аналогично). Тогда рассмотрим произвольную точку  и приращения
и приращения 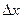 такие, что
такие, что  . Если
. Если  , то
, то 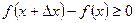 и
и  .
.
Если  , то
, то  , но все равно
, но все равно  . Предел
. Предел  существует и равен
существует и равен 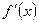 . По теореме 9.1 этот предел
. По теореме 9.1 этот предел  .
.
Обратно пусть для всех  выполняется неравенство
выполняется неравенство 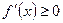 . Пусть
. Пусть  ,
,  . К отрезку
. К отрезку  можно применить теорему Лагранжа. Действительно, т.к.
можно применить теорему Лагранжа. Действительно, т.к. 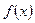 дифференцируема на
дифференцируема на 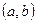 , то она непрерывна на
, то она непрерывна на 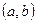 , а, значит, и на
, а, значит, и на  . Также по условию она дифференцируема на
. Также по условию она дифференцируема на  . Следовательно,
. Следовательно,  .►
.►
Теорема 29.1 допускает уточнение
◄Как и в предыдущей теореме, получаем, что для любых  ,
,  , имеет место неравенство
, имеет место неравенство
 .►
.►
Замечание. Утверждать, что если функция возрастает, то для всех  выполняется неравенство
выполняется неравенство  нельзя. Пример функции
нельзя. Пример функции  показывает, что хотя эта функция возрастает на всей прямой, есть точка
показывает, что хотя эта функция возрастает на всей прямой, есть точка  , в которой ее производная равна 0.
, в которой ее производная равна 0.
Таким образом, даже возрастание функции 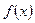 гарантирует, по теореме 29.1, лишь нестрогое неравенство
гарантирует, по теореме 29.1, лишь нестрогое неравенство 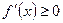 .
.
В теореме 23.1 установлено необходимое условие экстремума: Если функция 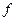 имеет производную
имеет производную  в точке экстремума
в точке экстремума 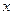 , то
, то  .
.
Как показывает пример из предыдущего замечания,  , это условие не является достаточным.
, это условие не является достаточным.
|
|
Дата добавления: 2015-04-24; Просмотров: 370; Нарушение авторских прав?; Мы поможем в написании вашей работы!