Лекции 19-20. Нормальные системы дифференциальных уравнений

Система дифференциальных уравнений – это система уравнений относительно независимой переменнойx, функций этой переменной и их производных . Система может быть записана в общем виде

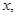
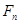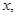
( )=0

....................................................................

( )=0

Порядок этой системы равен .

Пользуясь теоремой о неявной функции, можно разрешить систему уравнений относительно старших производных и записать ее в каноническом виде:

( )

..................................................................................

( )

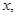
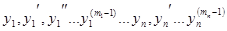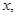
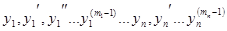Теорема. Любое дифференциальное уравнение, разрешенное относительно старшей производной, можно свести к системе дифференциальных уравнений первого порядка.

Доказательство. Рассмотрим дифференциальное уравнение n-ого порядка

. Обозначим . Дифференциальное уравнение n-ого порядка удалось свести к системе n дифференциальных уравнений первого порядка

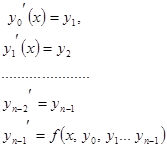
Применяя эту теорему, можно от канонического вида системы дифференциальных уравнений перейти к системе дифференциальных уравнений первого порядка - нормальному виду системы.

................

.........................................................................................

.................

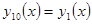
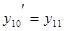
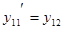
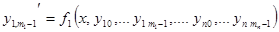
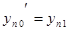
Получена система из дифференциальных уравнений первого порядка.

Удобнее нормальную систему дифференциальных уравнений (систему в нормальной форме) записывать в виде:

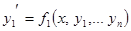
.................................. (покоординатная форма)

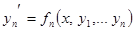
или в виде

, где (векторная форма).

Пример. 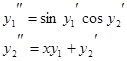Эти уравнения сводятся к нормальной системе

()

()

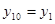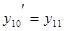
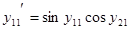
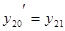
Оказывается, не только дифференциальное уравнение n- ого порядка сводится к системе n дифференциальных уравнений первого порядка – нормальной системе, но и нормальная система может быть сведена к одному дифференциальному уравнению.

Теорема. Пусть задана система n дифференциальных уравнений первого порядка

..................................

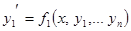
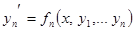
Обозначим

...................................

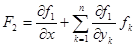
Потребуем, чтобы функция была бы дифференцируемой по совокупности переменных. Потребуем, чтобы определитель

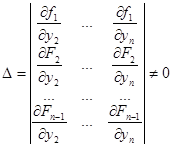
Тогда система n дифференциальных уравнений эквивалентна одному дифференциальному уравнению n-ого порядка.

Доказательство. Метод доказательства называется методом исключения переменных и применяется на практике при сведении системы к одному уравнению. Продифференцируем :

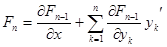
1) Построим алгоритм метода исключения.

Пусть 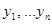- решения системы (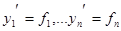), тогда уравнения системы представляют собой тождества

...................................

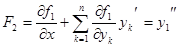
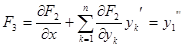
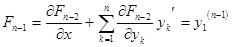
Получены выражения производных

,

,

,

...

.

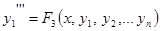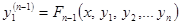Из этих уравнений можно выразить через 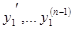, так как определитель системы этих уравнений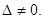

Подставим выражения через 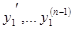в последнее уравнение . Так как 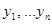- решения системы 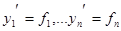, то они являются и решениями полученного уравнения. Следовательно, система 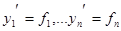сведена к одному уравнению n-ого порядка.

2) Покажем эквивалентность решений. Предположим, что 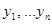- решения полученного уравнения, покажем, что 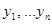- решения системы.

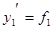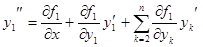, . Обозначим . . Обозначим , и т.д. 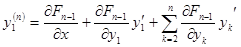. Обозначим .

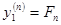Приравниваем полученные здесь функции введенным ранее, сокращая первые и вторые слагаемые, получаем систему уравнений

.....................................

.

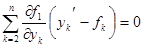
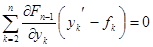Определитель этой системы равен 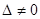, следовательно, в качестве единственного решения системы имеем . Поэтому решения эквивалентны. Теорема доказана.

Пример.

,

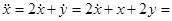
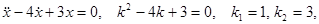
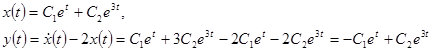
Функция 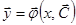называется общим решением системы, если

1. для любого 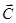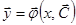- решение системы

2. для произвольных начальных условий найдется 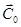, что .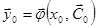

Если зафиксировать 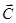в общем решении, получим частное решение системы.

Задача Коши.

Найти решение системы , удовлетворяющее заданным начальным условиям .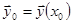

Теорема Коши о существовании и единственности решения задачи Коши

Пусть функция непрерывна по совокупности переменных. Пусть существуют и непрерывны частные производные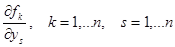

Тогда существует и единственно решение задачи Коши.

Дата добавления: 2015-04-24