
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Упражнения. I. Найти частные производные следующих функций по каждой из независимых переменных
I. Найти частные производные следующих функций по каждой из независимых переменных.
1)  ; 2)
; 2)  ; 3)
; 3) 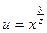 ; 4)
; 4)  ; 5)
; 5) 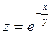 ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8) 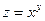 ; 9)
; 9)  .
.
II. Найти 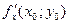 и
и  , если:
, если:
1)  ,
, 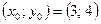 ; 2)
; 2) 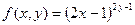 ,
, 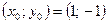 ; 3)
; 3)  ,
, 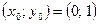 .
.
III. Верны ли следующие утверждения.
1) Если функция f (x, y) в точке (x 0, y 0) имеет частные производные, то она непрерывна в этой точке.
2) Если функция f (x, y) имеет частные производные в каждой точке (x 0, y 0) плоскости, то она непрерывна на плоскости.
3) Если функция f (x, y) дифференцируема в некоторой точке, то в этой точке она имеет частные производные.
4) Если в точке (x 0, y 0) функция f (x, y) не дифференцируема, то она разрывна в этой точке.
5) Если функция f (x, y) имеет в некоторой точке частные производные и она непрерывна на плоскости, то она дифференцируема в этой точке.
6) Если функция f (x, y) дифференцируема в некоторой точке, то в этой точке она имеет непрерывные частные производные.
7) Если функция f (x, y) имеет в окрестности точки (x 0, y 0) частные производные и они непрерывны в этой точке, то она дифференцируема в точке (x 0, y 0).
8) Если функция f (x, y) непрерывна в окрестности точки (x 0, y 0) и имеет там частные производные, то она дифференцируема в точке (x 0, y 0).
IV. Найти полный дифференциал функции u.
1) 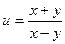 ; 2)
; 2) 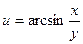 ; 3)
; 3)  ; 4)
; 4) 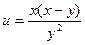 ; 5)
; 5)  ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8) 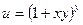 .
.
V. Пользуясь определением, доказать, что функция u дифференцируема в своей области определения и найти ее дифференциал.
1) u = xyz; 2)  .
.
VI. Доказать, что функция  не дифференцируема в точке (0; 0).
не дифференцируема в точке (0; 0).
VII. Написать уравнения касательной плоскости и нормали к поверхности z в заданной точке M 0.
1) 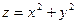 ,
,  ; 2)
; 2) 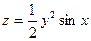 ,
,  ; 3)
; 3)  ,
,  ; 4)
; 4)  ,
,  .
.
VIII. Является ли дифференцируемой в точке О (0; 0) функция  ?
?
IX. Исследовать на дифференцируемость в точке О (0; 0) функцию 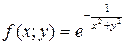 при
при 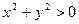 и
и  .
.
X. Найти решение  уравнения
уравнения
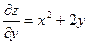 ,
,
удовлетворяющее условию 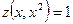 .
.
Тема 5. Дифференцирование композиции ФНП. Инвариантность формы записи дифференциала первого порядка
Теорема 1. Если функции  и
и  дифференцируемы в точке
дифференцируемы в точке  , а функция
, а функция  дифференцируема в соответствующей точке
дифференцируема в соответствующей точке  , то сложная функция
, то сложная функция  имеет в точке
имеет в точке 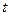 конечную производную по
конечную производную по 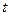 , причем справедлива формула
, причем справедлива формула
 . .
| (1) |
В частном случае, когда 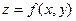 ,
,  и x – независимая переменная, при выполнении условий теоремы 1 формула (1) принимает вид
и x – независимая переменная, при выполнении условий теоремы 1 формула (1) принимает вид

| (2) |
Здесь 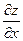 – частная производная по аргументу x функции
– частная производная по аргументу x функции 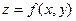 , а
, а 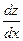 – полная производная функции
– полная производная функции 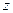 по x, т.е. обычная производная по x функции
по x, т.е. обычная производная по x функции  одной переменной x.
одной переменной x.
Теорема 2. Если функции  и
и  имеют в точке
имеют в точке  конечные частные производные
конечные частные производные  и в соответствующей точке
и в соответствующей точке  функция
функция  дифференцируема, то сложная функция
дифференцируема, то сложная функция  имеет в точке
имеет в точке  конечные частные производные, причем справедливы равенства
конечные частные производные, причем справедливы равенства

| (3) |
Теорема 3. Пусть в точке  функции
функции  и
и 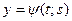 имеют непрерывные частные производные по
имеют непрерывные частные производные по 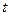 и по
и по  , а функция
, а функция  в окрестности соответствующей точки
в окрестности соответствующей точки  имеет частные производные
имеет частные производные 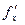 и
и  , непрерывные в этой точке. Тогда сложная функция
, непрерывные в этой точке. Тогда сложная функция 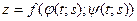 имеет непрерывные частные производные по
имеет непрерывные частные производные по 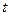 и по
и по  и дифференцируема в точке
и дифференцируема в точке  , а ее полный дифференциал имеет инвариантную форму
, а ее полный дифференциал имеет инвариантную форму
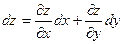 . .
| (4) |
Здесь 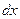 и
и 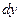 – дифференциалы функций
– дифференциалы функций  и
и 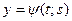 соответственно.
соответственно.
Форма записи (4) полного дифференциала сложной функции такая же, как и в случае независимых переменных  и
и 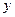 . В этом заключается свойство инвариантности формы записиполного дифференциала функции двух переменных.
. В этом заключается свойство инвариантности формы записиполного дифференциала функции двух переменных.
При соответствующих предположениях в случае сложной функции 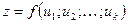 , где
, где 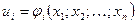 ,
,  , полный дифференциал функции
, полный дифференциал функции 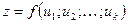 имеет инвариантную форму
имеет инвариантную форму
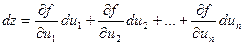 ,
,
причем для частных производных 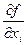 справедливы формулы, аналогичные формулам (3).
справедливы формулы, аналогичные формулам (3).
Пример 1. Составить, если это возможно, композицию 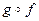 функций
функций  и
и 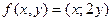 .
.
Решение. Для существования сложной функции 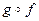 множество значений функции f должно содержать область определения функции g. Это условие выполняется, поскольку
множество значений функции f должно содержать область определения функции g. Это условие выполняется, поскольку  .
.
Тогда
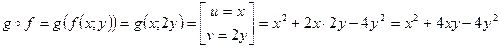 .
.
Пример 2. Найти все частные производные по независимым переменным x, y композиции z = g 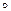 f, если
f, если  ,
, 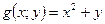 .
.
Решение. В композиции 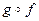 промежуточные переменные u и v определяются равенствами
промежуточные переменные u и v определяются равенствами  ,
,  . Для функций
. Для функций  ,
,  ,
,  выполняются все условия теоремы 2, поэтому искомые частные производные найдем по формулам (3).
выполняются все условия теоремы 2, поэтому искомые частные производные найдем по формулам (3).
Имеем
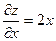 ;
;  ;
;  ;
; 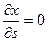 ;
;  ;
;  .
.
 ;
;  .
.
Пример 3. По формуле дифференцирования сложной функции найти 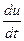 , если
, если  , где
, где 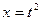 ,
,  ,
,  .
.
Решение. Указанная производная, очевидно, существует в любой точке t > 0. Для ее вычисления воспользуемся формулой
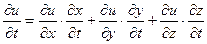 .
.
Так как
 ,
,  ,
, 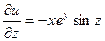 ,
,  ,
, 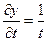 ,
, 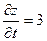 ,
,
то

 .
.
Пример 4. Найти 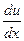 , если
, если  , где
, где 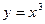 ,
, 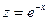 .
.
Решение. По формуле полной производной

при 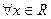 имеем
имеем

 .
.
Заметим, что этот же результат имеет место, если представить данную сложную функцию в виде  и воспользоваться правилами дифференцирования функций одной переменной.
и воспользоваться правилами дифференцирования функций одной переменной.
Пример 5. По формулам дифференцирования сложной функции найти частные производные 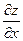 и
и  , если
, если  , где
, где  ,
,  .
.
Решение. Искомые частные производные, как легко видеть, существуют в любой точке 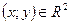 , причем
, причем
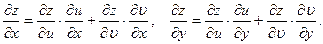
Так как
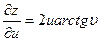 ,
,  ,
, 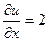 ,
,  ,
, 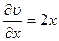 ,
,  ,
,
то
 ;
;
 .
.
Пример 6. Преобразовать к полярным координатам уравнение
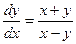 . .
| (5) |
Решение. Задача заключается в получении с помощью формул 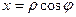 ,
, 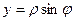 перехода к полярным координатам из уравнения (5), записанного для переменных x и y, равносильного ему уравнения, содержащего новые переменные r и j.
перехода к полярным координатам из уравнения (5), записанного для переменных x и y, равносильного ему уравнения, содержащего новые переменные r и j.
Пусть  – некоторая функция, удовлетворяющая уравнению (5). Будем рассматривать выражение в левой части уравнения (5) как отношение дифференциалов. Для их отыскания воспользуемся формулой дифференциала сложной функции. Это можно сделать, т.к. все частные производные
– некоторая функция, удовлетворяющая уравнению (5). Будем рассматривать выражение в левой части уравнения (5) как отношение дифференциалов. Для их отыскания воспользуемся формулой дифференциала сложной функции. Это можно сделать, т.к. все частные производные
 ,
,  ,
, 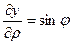 ,
, 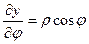
определены и непрерывны на R 2. В результате приходим к уравнению
 ,
,
из которого после элементарных преобразований имеем
 .
.
|
|
Дата добавления: 2015-04-24; Просмотров: 1295; Нарушение авторских прав?; Мы поможем в написании вашей работы!