Матрица передаточных функций

Модели стационарных линейных систем в комплексной плоскости на основе преобразования Лапласа

Известно, что преобразование Лапласа определяется парой преобразований

(2.6.1)

Первое из них называется прямым, а второе - обратным. Векторная функция 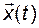называется оригиналом, а - изображением этого оригинала по Лапласу; - комплексная переменная преобразования Лапласа. Преобразование Лапласа можно осуществить, если и , где 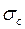- абсцисса абсолютной сходимости. Величина выбирается исходя из требования, чтобы функция при была абсолютно интегрируемой.

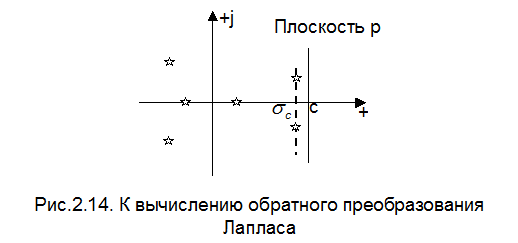
При вычислении обратного преобразования Лапласа интегрирование ведется на плоскости комплексной переменной p по прямой, параллельной мнимой оси, лежащей на прямой с, причем с выбирается так, чтобы все полюсы оказались слева от прямой интегрирования (рис. 2.14). На этом рисунке показано расположение полюсов некоторой функции .

Пусть, как обычно, уравнения объекта имеют вид

Перейдем к изображениям по Лапласу:

Перенесем AX(p) в левую часть равенства, а 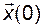- в правую:

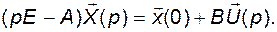
Отсюда получаем выражение для изображения вектора состояния

.

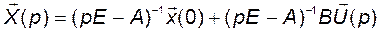Сравнивая это равенство с формулой Коши

,

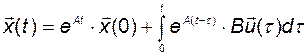отмечаем, что резольвента матрицы может рассматриваться как изображение по Лапласу от переходной матрицы (матричной экспо­ненты):

.

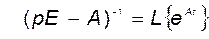Справедливо равенство

(2.6.2)

где 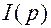- присоединенная матрица для матрицы А; - характеристический полином матрицы . 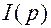и могут быть определены по методу Фаддеева - Леверье.

При нулевых начальных условиях

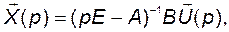(2.6.3)

где функция

(2.6.4)

называется матричной передаточной функцией от вектора управления до вектора выхода или передаточной функцией по каналу «u-x».

Аналогично при нулевых начальных условиях

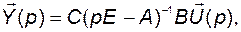(2.6.5)

где функция

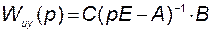(2.6.6)

называется матричной передаточной функцией от вектора управления до вектора выхода или передаточной функцией по каналу «u-y». Функцию 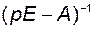называют резольвентой матрицы .

С использованием передаточной функции можно записать:

(2.6.7)

Принимая во внимание, что изображение по Лапласу - функции равно единице, можно представить передаточную функцию как изо­бра­жение от весовой функции

(2.6.8)

Передаточная функция является функцией от матрицы , поэтому в соответствии с (2.4.27) можно записать

(2.6.9)

и

. (2.6.10)

Графическое изображение последней формулы представлено в виде структурной схемы, изображённой на рис. 2.15.

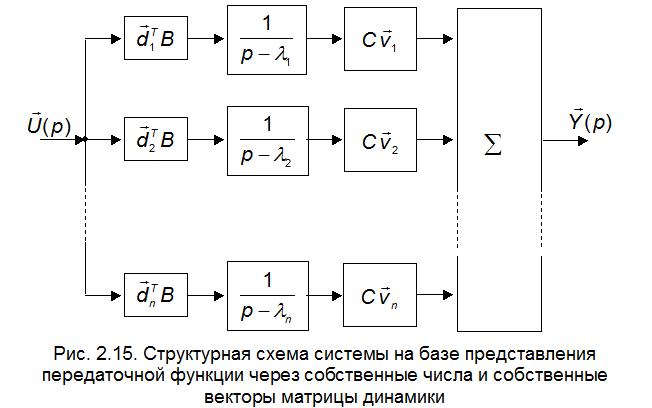
ПРИМЕР 2.6.1. Для объекта, схема в переменных состояния которого приведена на рис.2.16, уравнения состояния имеют вид

Им соответствуют матрицы

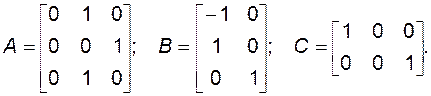
Характеристический полином имеет вид

.

Собственные числа

.

Присоединенная матрица

Резольвента

.

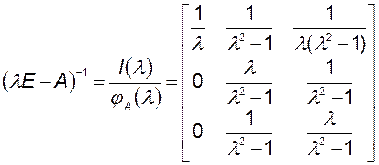В соответствии с (2.6.4) передаточная функция по вектору состояния

и по вектору выхода

.

Используя присоединенную матрицу, можно найти матрицу правых собственных векторов

.

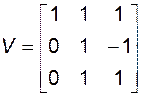Присоединенная матрица для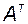

.

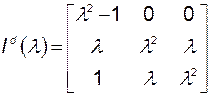Левые собственные векторы

.

Базовые матрицы

; ;

.

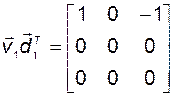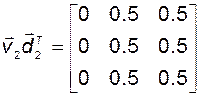Вычислим коэффициенты суммы (2.6.9):

; ;

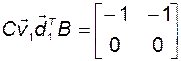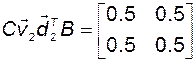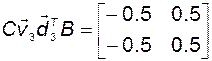
и получим результат, совпадающий, естественно, с уже полученным

.

Практически без дополнительных выкладок получаем

.

Интегрируя весовую функцию, получаем матричную переходную функцию

.

Дата добавления: 2015-03-31