Определение. Доказательство окончено

ОТЛИЧИМОСТЬ СОСТОЯНИЙ АВТОМАТОВ

Доказательство окончено.

Замечание. Если автомат Á, рассматриваемый в доказательстве теоремы, имеет n внутренних состояний, то можно считать, что r - s 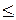n. Поэтому длина кратчайшего периода выходного сверхслова не превосходит значения n ´ | |.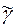

Состояния q _i и q _j автомата Á называются отличимыми, если существует такое входное слов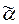о , что

() ().

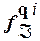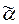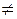
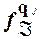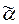Отличимость двух состояний q _i и q _j означает, что существует входное слово 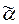, которое из этих состояний как начальных перерабатывается в разные выходные слова.

В качестве примера рассмотрим автомат, изображенный на рис. 7.6.

0 (0) 0 (0)

q₀ q ₁

0 (1) 1 (1) 1 (1)

1 (0) q₂

Рис. 7.6

Состояния q ₀ и q ₁ заданного автомата неотличимые. Это так поскольку первый символ произвольного входного слова 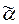из состояний q ₀ и q ₁ как начальных перерабатывается одинаково. При этом автоматв обоих случаях переходит в одно и то же состояние. Поэтому дальнейшая переработка слова 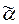из начальных состояний q ₀и q ₁ продолжается одинаково.

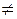
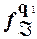Состояния q ₀ и q ₂ рассматриваемого автомата являются отличимыми так как, например, (0) (0).

Если состояния q _i и q _j автомата - являются отличимыми, то функци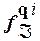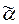и () и 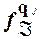(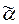) различаются на бесконечном множестве слов.

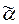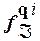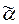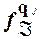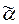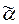
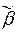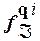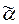
Действительно, если для некоторого имеет место соотношение () ¹ (), то для любого слова также справедливо ( 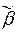) |¹ ( ).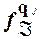

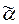
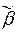Функции, вычисляемые автоматами, имеют бесконечные области определения. Поэтому невозможна конструктивная проверка отличимости состояний на основе только определения отличимости.

С целью отыскания метода для распознавания отличимых состояний произвольных автоматов рассмотрим вопрос о длине кратчайшего слова, которое по-разному перерабатывается из двух отличимых состояний q _i и q _j. Прежде всего отметим, что длина кратчайшего слова может быть сколь угодно большой.

Пусть Á - это автомат с n состояниями, диаграмма переходов которого приведена на рис. 7.7.

0 (0) 0 (0) 0 (0)

0 (0)

q₁q ₂ .... q _n

1 (1) 1 (1) 1 (1)

1 (0)

Рис 7.7

Состояния q ₁ и q ₂ этого автомата являются отличимыми, и длина кратчайшего слова, на котором они различаются, равна n - 1.

Действительно, для любого входного слова 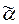первые n - 1 символов этого слова одинаково перерабатываются автоматом из состояний q ₁ и q _2. После этого Á переходит в состояние q _n, если он начал работу из состояния q ₂, и в состояние q _{n- 1}, если Á начинает работу из состояния q _1. Из q _{n- 1} и q _n как начальных состояний всякое односимвольное слово перерабатывается по-разному. Поэтому n -й символ любого входного слова 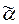перерабатывается из состояний q ₀и q ₁ в разные выходные слова.

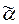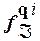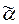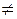
Покажем, что если состояния q _i и q _j автомата Á, имеющего n состояний, отличимые, и - это кратчайшее слово, для которого () 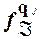(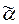), то | 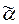| 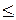n - 1.

Дата добавления: 2015-03-31