Билет 1. Скалярное произведение векторов

Скалярное произведение векторов. Свойства.-операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длинывектора x на проекцию вектора y на вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю. Свойства

Векторное произведение. Свойства. Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Произведение не является ни коммутативным, ни ассоциативным (оно является антикоммутативным) и отличается от скалярного произведения векторов. Геометрические свойства векторного произведения

Уравнение окружности. Окружность — геометрическое место всех точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное неотрицательное расстояние, называемое её радиусом. Уравнения

Базис векторного пространства. Переход к новому базису. множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества — базисных векторов. Переход к новому базису

В старом базисе 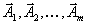мы имели следующие разложения векторов по этому базису

(8)

Теперь мы перешли в новую вершину, которой соответствует базис и, чтобы иметь возможность двигаться дальше к следующей вершине, мы должны иметь разложения векторов 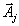по этому новому базису, то есть

.

(9)

Выведем формулы для . Мы должны вывести из базиса вектор 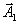и ввести туда вектор 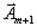. Поэтому возьмём выражение для вектора (5)

,

выразим из него вектор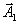

и подставим это выражение в (8). Тогда мы получим

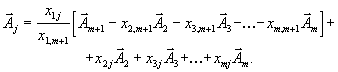
Перегруппировывая слагаемые, получим:

Таким образом, координаты вектора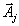

в новом базисе имеют вид

(10)

что и дает разложение векторов по новому базису.

[править]Декартовы координаты

Окружность радиуса r = 1, центр (a, b) = (1.2, −0.5)

Общее уравнение окружности записывается как:

или

где

Точка — центр окружности, — её радиус.

Уравнение окружности радиуса с центром в начале координат:

Уравнение окружности, проходящей через три точки (с помощью определителя) и

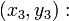
Окружность также можно описать с помощью параметрического уравнения:

В декартовой системе координат окружность не является графиком функции, но она может быть описана как объединение графиков двух следующих функций:

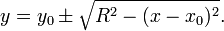
Если центр окружности совпадает с началом координат, функции принимают вид:

Билет № 14

1. Миноры матрицы. Минор-определитель такой квадратной матрицы 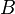порядка (который называется также порядком этого минора), элементы которой стоят в матрице на пересечении строк с номерами и столбцов с номерами .

Если номера отмеченных строк совпадают с номерами отмеченных столбцов, то минор называется главным, а если отмечены первые k строк и первые k столбцов ― угловым или ведущим главным.

2. Собственные значения линейного оператора. Если имеет место равенство:

то называют собственным значением оператора , а функцию 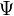— собственной функцией оператора 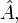соответствующей данному собственному значению. Чаще всего у оператора имеется множество собственных значений: Множество всех собственных значений называется спектром оператора.

Билет № 15

1. Алгебраическое дополнение элемента матрицы. Алгебраическим дополнением элемента 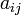матрицы называется число

,

где 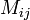— дополнительный минор, определитель матрицы, получающейся из исходной матрицы путем вычёркивания i -й строки и j -го столбца.

2. Собственные векторы линейного оператора. Собственным вектором линейного преобразования называется такой ненулевой вектор 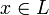, что для некоторого

Собственным значением линейного преобразования называется такое число , для которого существует собственный вектор, то есть уравнение имеет ненулевое решение .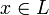

Упрощённо говоря, собственный вектор — любой ненулевой вектор x, который отображается оператором в коллинеарный 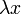, а соответствующий скаляр 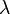называется собственным значением оператора.

Билет № 16

1.Матричные уравнения. Их решение. Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.

Пусть дана система линейных уравнений с 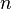неизвестными (над произвольным полем):

Тогда её можно переписать в матричной форме:

, где — основная матрица системы, 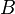и — столбцы свободных членов и решений системы соответственно:

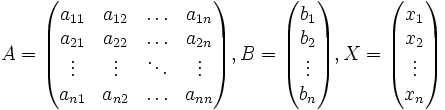
Умножим это матричное уравнение слева на — матрицу, обратную к матрице :

Так как , получаем 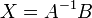. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:

.

Для однородной системы линейных уравнений, то есть когда вектор 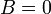, действительно обратное правило: система имеет нетривиальное (то есть ненулевое) решение только если . Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.

· Необходимым и достаточным условием коллинеарности двух ненулевых векторов является равенство нулю их векторного произведения.

· Модуль векторного произведения равняется площади параллелограмма, построенного на приведённых к общему началу векторах и (см. Рисунок 1)

· Если — единичный вектор, ортогональный векторам и и выбранный так, что тройка — правая, а 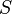— площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула:

· Если — какой-нибудь вектор, — любая плоскость, содержащая этот вектор, — единичный вектор, лежащий в плоскости и ортогональный к , — единичный вектор, ортогональный к плоскости и направленный так, что тройка векторов является правой, то для любого лежащего в плоскости вектора справедлива формула

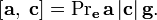
· При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c (см. Рисунок 2). Такое произведение трех векторов называетсясмешанным.

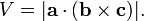
На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:

Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов также, как и скалярное произведениеможет рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0 (нулевому вектору), если векторы параллельны либо антипараллельны.

[править]Алгебраические свойства векторного произведения

Представление	Описание
	свойство антикоммутативности
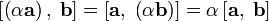
	свойство ассоциативности относительно умножения на скаляр
	свойство дистрибутивности по сложению
	тождество Якоби, выполняется в и нарушается в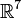
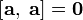
	формула «БАЦ минус ЦАБ», тождество Лагранжа
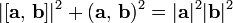
	Это частный случай мультипликативности нормы кватернионов
	значение этого выражения называют смешанным произведением векторов , , и обозначают либо

Билет № 17

1.Теорема Лапласа. Пусть выбраны любые строк матрицы . Тогда определитель матрицы равен сумме всевозможных произведений миноров -го порядка, расположенных в этих строках, на их алгебраические дополнения.

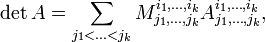
где суммирование ведётся по всевозможным номерам столбцов

2.Смешенное произведение векторов. Свойства. Сме́шанное произведе́ние векторов 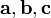— скалярное произведение вектора на векторное произведение векторов и :

.

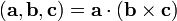Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).

· Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами 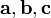. Смешанное произведение кососимметрично по отношению ко всем своим аргументам:

т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что

· Смешанное произведение в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов и :

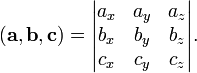
· Смешанное произведение в левой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов и , взятому со знаком «минус»:

В частности,

· Если какие-то два вектора коллинеарны, то с любым третьим вектором они образуют смешанное произведение, равное нулю.

· Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.

· Геометрический смысл — Смешанное произведение по абсолютному значению равно объёму параллелепипеда (см. рисунок), образованного векторами и ; знак зависит от того, является ли эта тройка векторов правой или левой.

· Квадрат смешанного произведения векторов равен определителю Грама, определяемому ими^.

· Смешанное произведение удобно записывается с помощью символа (тензора) Леви-Чивита:

(в последней формуле в ортонормированном базисе все индексы можно писать нижними; в этом случае эта формула совершенно прямо повторяет формулу с определителем, правда, при этом автоматически получается множитель (-1) для левых базисов).

Билет №18

1. Теорема Кронекера-Капелли. Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

· теорема косинусов легко выводится с использованием скалярного произведения:

· Угол между векторами:

· Оценка угла между векторами:

в формуле знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение > 0, если угол между векторами острый, и < 0, если угол между векторами тупой.

· Проекция вектора на направление, определяемое единичным вектором :

,

· условие ортогональности^[2] (перпендикулярности) векторов и :

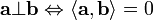
· Площадь параллелограмма, натянутого на два вектора и , равна

Билет №19

1.Линейнонезависимые строки матрицы. Система строк называется линейно независимой (ЛНЗ), если только тривиальная Линейная Комбинация равна нулевой строке. Линейной комбинацией (ЛК) строк матрицы называется выражение

ЛК называется тривиальной, если все коэффициенты равны нулю одновременно.

2.Квадратичная форма. Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора. Критерий Сильвестра определяет, является ли симметричная квадратная матрица положительно (отрицательно, неотрицательно) определённой.

Пусть квадратичная форма имеет в каком-то базисе матрицу

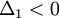Тогда эта форма положительно определена, тогда и только тогда когда все её главные (угловые) миноры положительны. Форма отрицательно определена, если и только если знаки чередуются, причём . Здесь главными минорами матрицы называются определители вида

Для неотрицательно определённых матриц критерий действует только в одну сторону: если форма неотрицательно определена, то главные миноры неотрицательны. Обратное неверно. Например, матрица

не является неотрицательно определённой — так как, например, для . В то же время все её главные миноры равны 0, то есть неотрицательны.

Билет №20

1. Преобразования определителя матрицы.

2. Корни системы линейных уравнений

Вопрос 1.

Фиктивное банкротство как уголовно-наказуемое деяние.

Фиктивное банкротство, то есть заведомо ложное объявление руководителем или собственником коммерческой организации, а равно индивидуальным предпринимателем о своей несостоятельности в целях введения кредиторов в заблуждение для получения отсрочки или рассрочки причитающихся кредиторам платежей, а равно для неуплаты долгов, если это деяние причинило ущерб - то наказывается штрафом в размере от 100 до 300 тыс.руб или в размере з/п или иного дохода осужденного за период до 2 лет или лишение свободы сроком до 6 лет со щтрафом в размере 8 т.р. или в размере з/п за период до 6 мес.

Порядок определения признаков фиктивного банкротства

Для установления наличия (отсутствия) признаков фиктивного банкротства проводится анализ значений и динамики коэффициентов, характеризующих платежеспособность должника, рассчитанных за исследуемый период в соответствии с правилами проведения арбитражными управляющими финансового анализа, утвержденными Правительством Российской Федерации.

В случае если анализ значений и динамики коэффициента абсолютной ликвидности, коэффициента текущей ликвидности, показателя обеспеченности обязательств должника его активами, а также степени платежеспособности по текущим обязательствам должника указывает на наличие у должника возможности удовлетворить в полном объеме требования кредиторов по денежным обязательствам и (или) об уплате обязательных платежей без существенного осложнения или прекращения хозяйственной деятельности, делается вывод о наличии признаков фиктивного банкротства должника.

В случае если анализ значений и динамики соответствующих коэффициентов, характеризующих платежеспособность должника, указывает на отсутствие у должника возможности рассчитаться по своим обязательствам, делается вывод об отсутствии признаков фиктивного банкротства должника.

Дата добавления: 2015-04-24