Квадратичные формы: определения, свойства, теоремы

Нахождение собственных значений и собственных векторов по матрице оператора

Теорема. Вещественное число λ является собственным значением линейного оператора А: X_n → X_n тогда и только тогда, когда λ удовлетворяет уравнению

det (A − λE) = 0,

(1)

где A — квадратная матрица n –го порядка — матрица оператора А в некотором базисе, а E — единичная матрица того же порядка, что и A.

Доказательство. Пусть вектор x — собственный вектор оператора А, соответствующий собственному значению λ, т.е. по определению

А(x) = λ(x), А(x)= λ Е(x), (А− λ Е) x = θ.

Следовательно, чтобы найти собственные значения и собственные векторы оператора А, нужно решить однородную систему n линейных уравнений с n неизвестными (A − λE)X = O.

Так как по определению собственного вектора x ≠ θ, то нас интересуют лишь нетривиальные решения этой системы уравнений. Необходимым и достаточным условием нетривиальной совместности однородной системы n уравнений с n неизвестными является условие det (A − λE) = 0, что и требовалось доказать.

Уравнение (1) называется характеристическим уравнением оператора А.

Т1: Если матрица лин. оператора в некотором базисе имеет диагональный вид, то все векторы этого базиса являются собственными векторами лин. оператора, а числа на главной диагонали являются собственными значениями.

Т2: Если лин. оператор имеет n различных собственных значений, то все его собственные векторы линейно независимы и матрица лин. оператора в этом базисе имеет диагональный вид.

Собственные значения и векторы не зависят от базиса.

Определение. Квадратичной формой переменных ,принимающих числовые значения, называется числовая функция вида

,

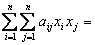
где - числа, называемые коэффициентами квадратичной формы.(квадратичная форма - в n-мерном пространстве L(x₁,x₂,…x_n)-сумма, каждое слагаемое которой либо квадрат одной из переменных, либо произведение двух различных переменных, взятых с коэффициентом)

Определение. Матрицей квадратичной формы переменных , называется симметрическая матрица порядка , элементы главной диагонали которой совпадают с коэффициентами при квадратах переменных, а каждый недиагональный элемент, расположенный в ой строке 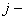ом столбце, равен половине коэфициента при в квадратичной форме.

Определение. Рангом квадратичной формы называется ранг её матрицы. Квадратичная форма может быть записана в матричном виде где матрица квадратичной формы и .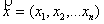

Определение. Квадратичная форма называется канонической (имеет канонический вид), если коэфициенты 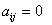при , то есть, если матрица квадратичной формы диагональная и следовательно

.,

где не все коэффициенты равны нулю.

Теорема (Лагранжа). Для всякой квадратичной формы существует такой базис, в котором квадратичная форма имеет канонический вид.

Определение. Нормальным видом квадратичной формы называется такой канонический вид, в котором коэффициенты при квадратах неизвестных (не считая нулевых) равны .

Определение. Квадратичная форма 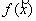называется положительно

(отрицательно) определённой, если 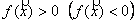при всех

и положительно (отрицательно) полуопределённой,если 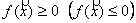при всех .

Теорема (критерий Сильвестра). Для того чтобы квадратичная форма 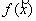была положительно определённой, необходимо и достаточно чтобы все угловые миноры матрицы квадратичной формы были положительны, то есть, чтобы

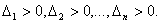
Здесь 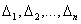-угловые миноры матрицы квадратичной формы.

Следствие. Для того чтобы квадратичная форма 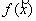была отрицательно определённой, необходимо и достаточно, чтобы знаки угловых миноров матрицы квадратичной формы чередовались следующим образом:

Определение квадратичной формы

Квадратичная форма переменных - функция

- коэффициенты квадратичной формы. Без ограничения общности считают 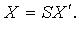тогда

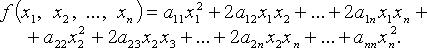
Если переменные принимают действительные значения и 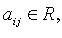квадратичная форма называется действительной.

Матричная запись квадратичной формы

Матрица

называется матрицей квадратичной формы, ее ранг - рангом квадратичной формы. Квадратичная форма называется невырожденной, если

Главные миноры матрицы A называются главными минорами квадратичной формы.

В пространстве квадратичную форму можно записать в виде 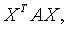где X - координатный столбец вектора

В пространстве 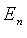квадаратичную форму можно представить в виде 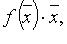где f - линейный самосопряженный оператор, матрица которого в некотором ортонормированном базисе равна A.

Дата добавления: 2015-04-24