Перехід від одного опорного плану до іншого

VI. ВИКОРИСТАНІ ЛІТЕРАТУРНІ ДЖЕРЕЛА.

ОСНОВНІ:

1. Криворучко П.П. Історія психології: Навч.посібн.- К.: Кондор, 2009.- 232с.

3. Корольчук М.С., Криворучко П.П. Історія психології: Навч. посіб.- К.: Ельга Ніка Центр, 2010.- 248с.

4. Маноха І.П., Роменець В.А. Історія психології ХХ століття: Навч. посіб. для ВНЗ.- К.: Либідь,2007.- 832с.

5. Марцинковская Т.Д. История психологи.- М.: Академия,2009.-544с.

6. Роменець В. А. Історія психології: Стародавній світ. Середні віки. Відродження. - К.: Либідь, 2005.-243с.

ДОДАТКОВІ:

6.Жуков С. Історія психології: Навч. посіб./ Сергій Жуков, Тетяна Жукова; М-во освіти і науки України, Донецький ін.-т ринку та соціальної політики.- К.: Центр навчальної літератури, 2005.- 222с.

7. Смит Р. История гуманитарных наук:Пер. С англ.- М.:Издательский дом «ГУ- ВШЭ», 2007.- 392с.

8. Смит Р. История психологии: учебн. пособие для студ. высш. учеб. завед. -М.: Издательский центр «Академия», 2008.- 416с.

9. Основи психології: Підручник // За заг. ред. О.В. Киричука, В.А.Роменця.- Вид.6-те, стереотип.- К.: Либідь, 2006.- 632с.

ЕЛЕКТРОННІ:

1. Альманах психологических тестов. – М. 1995. - Електронний ресурс / Режим доступу: http://www.vashpsixolog.ru/psychodiagnostic-school-psychologist/61-diagnosis-of-intellectual-development/487-methods-committing-10-words

Додаток 1

МІНІСТЕРСТВО ОХОРОНИ ЗДОРОВ’Я УКРАЇНИ

ОДЕСЬКИЙ НАЦІОНАЛЬНИЙ МЕДИЧНИЙ УНІВЕРСИТЕТ

КАФЕДРА СОЦІАЛЬНОЇ ДОПОМОГИ, ЗАГАЛЬНОЇ ТА МЕДИЧНОЇ ПСИХОЛОГІЇ

РУБІЖНИЙ КОНТРОЛЬ №1

з дисципліни «Історія психології»

Варіант VІІ

Завдання для РК1 отримано: 2014.02.17

РК1 здано: 2014. ______________. «_____»

Виконав:

студент групи, 1-го курсу

медико-профілактичного факультету,

спеціальності 6.030103, «Практична психологія», заочної форми навчання,

Іваненко П.М.

Науковий керівник:

ас. кафедри СДЗМП ОНМедУ,

Стрельбицька С.М.

Одеса – 2014

[1] - Планування, виконання та облік роботи кафедри (інструктивні матеріали) / Упорядники: Ю.І.Бажора, В.Й.РКесюн, О.О.Мардашко, Г.В.Чернявська, Н.М.Олійник, Л.Я.Гриняєва / ОНМедУ, 2001. - С. 10.

[2] - Положення про КМСОНП в ОНМедУ: видання четверте, доповн. та переробл. / За ред. В.М.Запорожана / Кресюн В.Й., Бажора Ю.І., Гончарук С.Ф. та ін. – Одеса: ОНМедУ, 2013. – 38 с.

Розглянемо, як, виходячи з початкового опорного плану (2.40), перейти до наступного опорного плану, що відповідає ціле­спрямованому процесу перебору кутових точок багатогранника розв’язків.

Оскільки 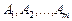є базисом m -вимірного простору, то кожен з векторів співвідношення (2.39) може бути розкладений за цими векторами базису, причому у єдиний спосіб:

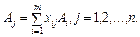
Розглянемо такий розклад для довільного небазисного вектора, наприклад, для :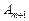

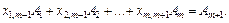(2.42)

Припустимо, що у виразі (2.42) існує хоча б один додатний коефіцієнт .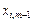

Введемо деяку поки що невідому величину 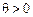, помножимо на неї обидві частини рівності (2.42) і віднімемо результат з рівності (2.41). Отримаємо:

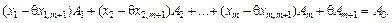(2.43)

Отже, вектор

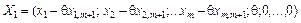
є планом задачі у тому разі, якщо його компоненти невід’ємні. За допущенням 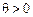, отже, ті компоненти вектора 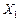, в які входять 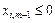, будуть невід’ємними, тому необхідно розглядати лише ті компоненти, які містять додатні 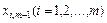. Тобто необхідно знайти таке значення 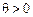, за якого для всіх 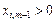буде виконуватися умова невід’ємності плану задачі:

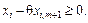(2.44)

З (2.44) отримуємо, що для шуканого 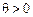має виконуватися умова 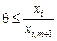. Отже, вектор 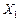буде планом задачі для будь-якого q, що задовольняє умову:

,

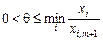де мінімум знаходимо для тих i, для яких .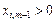

Опорний план не може містити більше ніж m додатних компонент, тому в плані 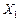необхідно перетворити в нуль хоча б одну з компонент. Допустимо, що 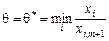для деякого значення і, тоді відповідна компонента плану 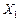перетвориться в нуль. Нехай це буде перша компонента плану, тобто:

.

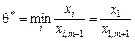Підставимо значення 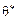у вираз (2.43):

,

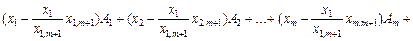
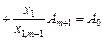якщо позначити 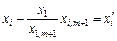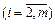, , 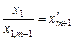то рівняння можна подати у вигляді:

,

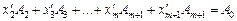якому відповідає такий опорний план:

.

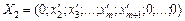Для визначення наступного опорного плану необхідно аналогічно продовжити процес: будь-який вектор, що не входить у базис, розкласти за базисними векторами, а потім визначити таке 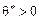, для якого один з векторів виключається з базису.

Отже, узагальнюючи розглянутий процес, можемо висновувати: визначення нових опорних планів полягає у виборі вектора, який слід ввести в базис, і вектора, який необхідно вивести з базису. Така процедура відповідає переходу від одного базису до іншого за допомогою методу Жордана—Гаусса.

Необхідно зазначити, що для випадку, коли вектор 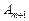підлягає включенню в базис, а в його розкладі (2.42) всі 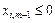, то, очевидно, не існує такого значення 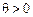, яке виключало б один з векторів. У такому разі план 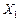містить m +1 додатних компонент, отже, система векторів 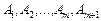буде лінійно залежною і визначає не кутову точку багатогранника розв’язків. Функціонал не може в ній набирати максимального значення. Це означає, що функціонал є необмеженим на багатограннику розв’язків.

2.8.3. Оптимальний розв’язок.
Критерій оптимальності плану

Симплексний метод уможливлює направлений перебір опорних планів, тобто перехід від одного плану до іншого, який є хоча б не гіршим від попереднього за значенням функціонала. Отже, окремим питанням стає вибір вектора, який необхідно вводити в базис при здійсненні ітераційної процедури симплексного методу.

Розглянемо задачу лінійного програмування (2.36)—(2.38).

Допустимо, що вона має опорні плани і вони є невиродженими. Розглянемо початковий опорний план виду (2.40):

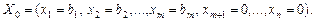
Такому плану відповідає розклад за базисними векторами

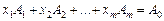(2.45)

та значення функціонала:

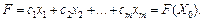(2.46)

Кожен з векторів 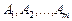можна розкласти за векторами базису, причому у єдиний спосіб:

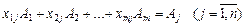, (2.47)

тому такому розкладу відповідатиме і єдине значення функ­ціонала:

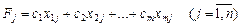. (2.48)

Позначимо через 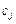коефіцієнт функціонала, що відповідає вектору 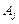, та 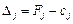(їх називають оцінками відповідних векторів плану) 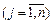. Тоді справедливим є таке твердження (умова оптимальності плану задачі лінійного програмування): якщо для деякого плану 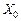розклад всіх векторів 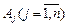у даному базисі задовольняє умову:

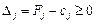, (2.49)

то план 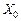є оптимальним розв’язком задачі лінійного програмування (2.36)—(2.38).

Аналогічно формулюється умова оптимальності плану задачі на відшукання мінімального значення функціонала: якщо для деякого плану 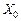розклад всіх векторів 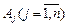у даному базисі задовольняє умову

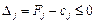, (2.50)

то план Х ₀ є оптимальним розв’язком задачі лінійного програмування.

Отже, для того, щоб план задачі лінійного програмування був оптимальним, необхідно і достатньо, щоб його оцінки 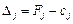були невід’ємними для задачі на максимум та недодатними для задачі на мінімум.

Умови оптимальності планів задач лінійного програмування є наслідками двох теорем. Скориставшись введеними в даному параграфі допущеннями та позначеннями, сформулюємо відповідні теореми, а також наведемо їх доведення.

Теорема 2.6. Якщо для деякого вектора 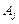виконується умова 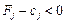, то план 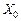не є оптимальним і можна відшукати такий план Х, для якого виконуватиметься нерівність .

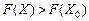Доведення. Помножимо (2.47) і (2.48) на 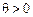і віднімемо результати відповідно з (2.45) та (2.46). Отримаємо:

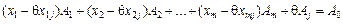; (2.51)

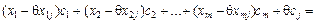
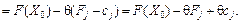(2.52)

У співвідношенні (2.52) до обох частин додається величина 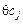для 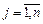. У (2.51) 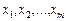додатні, тому завжди можна знайти таке 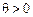, що всі коефіцієнти при векторах 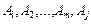були б невід’ємними, інакше кажучи, отримати новий план задачі виду:

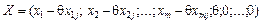, якому згідно з (2.52) відповідає таке значення функціонала:

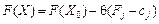. (2.53)

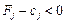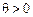Оскільки за умовою теореми і , то 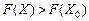, що й потрібно було довести.

Якщо розглядається задача на відшукання мінімального значення цільової функції, то формулюється така теорема.

Теорема 2.7. Якщо для деякого вектора 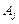виконується умова 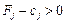, то план 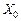не є оптимальним і можна побудувати такий план Х, для якого виконуватиметься нерівність .

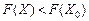Доведення аналогічне попередньому.

2.8.4. Розв’язування задачі
лінійного програмування симплексним методом

Розглянемо, як, виходячи з початкового опорного плану задачі лінійного програмування, за допомогою симплексного методу знайти оптимальний план.

Продовжимо розгляд задачі (2.36)—(2.38), опорний план якої 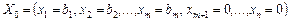. Для дослідження даного плану на оптимальність (за умовою оптимальності плану задачі лінійного програмування) необхідно вектори 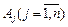системи обмежень (2.37) розкласти за базисними векторами 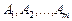і розрахувати значення оцінок .

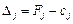Всі подальші обчислення зручно проводити в симплексній таблиці (табл. 2.6).

У стовпці «Базис» записані змінні, що відповідають базисним векторам, а в стовпці «С_баз» — коефіцієнти функціонала відповідних базисних векторів. У стовпці «План» — початковий опорний план 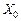, в цьому ж стовпці в результаті обчислень отримують оптимальний план. У стовпцях 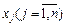записані коефіцієн­ти розкладу кожного j -го вектора за базисом, які відповідають у пер­шій симплексній таблиці коефіцієнтам при змінних у системі (2.37). У (m + 1)-му рядку в стовпці «План» записують значення функціонала для початкового опорного плану 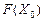, а в інших стовпцях 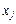— значення оцінок 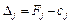. Цей рядок симплексної таблиці називають оцінковим.

Значення 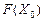знаходять підстановкою компонент опорного плану в цільову функцію, а значення 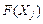— при підстанов­ці коефіцієнтів розкладу кожного j -го вектора за векторами ба­зису, тобто ці значення в табл. 2.6 отримують як скалярний добуток:

,

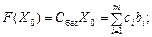
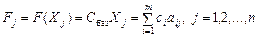де с_і — коефіцієнти функціонала, що відповідають векторам базису.

Таблиця 2.6

ПЕРША СИМПЛЕКСНА ТАБЛИЦЯ ДЛЯ РОЗВ’ЯЗКУ ЗАДАЧ
ЛІНІЙНОГО ПРОГРАМУВАННЯ

і

Базис

Сбаз

План

c 1

c 2

…

cl

…

cm

cm + 1

…

cj

…

ck

…

cn

θ і

x 1

x 2

…

xl

…

xm

xm + 1

…

xj

…

xk

…

xn

x 1

c 1

b 1

…

…

a 1, m +1

…

a 1 j

…

a 1 k

…

a 1 n

θ1

2

x 2

c 2

b 2

…

…

a 2, m + 1

…

a 2 j

…

a 2 k

…

a 2 n

θ2

M

M

M

M

M

M

M

M

M

M

M

M

M

M

M

M

M

M

l

xl

cl

bl

…

…

al, m + 1

…

alj

…

alk

…

aln

θ l

M

M

M

M

M

M

M

M

M

M

M

M

M

M

M

M

M

M

m

xm

cm

bm

…

…

am, m + 1

…

amj

…

amk

…

amn

θ m

m + 1

Fj – cj ≥ 0

F (X 0)

…

…

Δ m + 1

…

Δ j

…

Δ k

…

Δ n

Після заповнення табл. 2.6 розраховують значення оцінок плану (останній рядок): 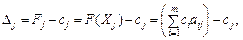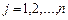. Потім згідно з умовою оптимальності плану задачі лінійного програмування, якщо всі 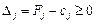(для задачі на максимум), то план є оптимальним. Допустимо, що одна з оцінок 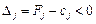, тоді план 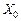не є оптимальним і необхідно здійснити перехід до наступного опорного плану, якому буде відповідати більше значення функціонала. Якщо від’ємних оцінок кілька, то включенню до базису підлягає вектор, який вибирається як 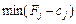. Мінімум знаходять для тих індексів j, де 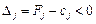. Якщо існує кілька однакових значень оцінок, що відповідають 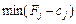, то з відповідних їм векторів до базису включають той, якому відповідає максимальне значення функціонала.

Якщо хоча б для однієї від’ємної оцінки 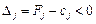всі коефіцієнти розкладу відповідного вектора недодатні, то це означає, що функціонал є необмеженим на багатограннику розв’язків, тобто багатогранник у даному разі являє собою необмежену область і розв’язком задачі є .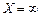

Нехай 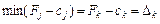, тобто мінімальне значення досягається для k -го вектора 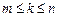. Тоді до базису включається вектор 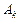. Відповідний стовпчик симплексної таблиці називають напрямним.

Для того, щоб вибрати вектор, який необхідно вивести з базису (згідно з процедурою переходу від одного опорного плану задачі до іншого — § 2.7.2), розраховують останній стовпчик табл. 2.6 — значення .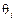

.

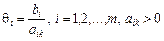З розрахованих значень необхідно вибрати найменше 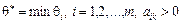. Тоді з базису виключають i -ий вектор, якому відповідає .

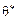Допустимо, що 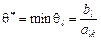відповідає вектору, що знаходиться в l -му рядку табл. 2.6. Відповідний рядок симплексної таблиці називають напрямним.

Перетином напрямного стовпчика та напрямного рядка визначається елемент симплексної таблиці a_lk, який називають розв’язувальним елементом. За допомогою елемента a_lk і методу Жордана—Гаусса розраховують нову симплексну таблицю, що визначатиме наступний опорний план задачі.

Для визначення нового опорного плану необхідно всі вектори розкласти за векторами нового базису. Вектор А_k, який необхідно вводити до базису, в розкладі за початковим базисом має вигляд:

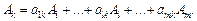(2.54)

Вектор А_l виходить з базису, і його розклад за новим базисом отримаємо з виразу (2.54):

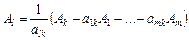. (2.55)

Розклад вектора А₀ за початковим базисом має вигляд:

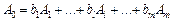. (2.56)

Для запису розкладу вектора в новому базисі підставимо вираз (2.55) у рівняння (2.56), маємо:

.

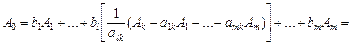
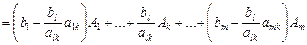Отже, значення компонент наступного опорного плану розраховуються за формулами:

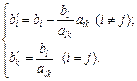(2.57)

Розклад за початковим базисом будь-якого з векторів має вигляд:

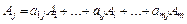. (2.58)

Розклад за новим базисом отримаємо підстановкою (2.55)
у (2.58):

.

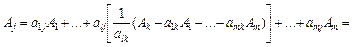
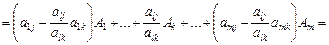
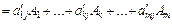Новий план: 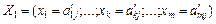, де

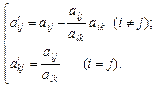(2.59)

Формули (2.57) та (2.59) є формулами повних виключень Жор­дана—Гаусса.

Отже, щоб отримати коефіцієнти розкладу векторів 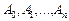за векторами нового базису (перехід до наступного опорного плану та створення нової симплексної табл. 2.7), необхідно:

1) розділити всі елементи напрямного рядка на розв’язуваль­ний елемент;

2) розрахувати всі інші елементи за формулами повних виключень Жордана—Гаусса (правило прямокутника).

Потім необхідно здійснити перевірку нових значень оцінкового рядка. Якщо всі F_j – с _j ³ 0, то план Х₁ — оптимальний, інакше переходять до відшукання наступного опорного плану. Процес продовжують до отримання оптимального плану, чи встановлення факту відсутності розв’язку задачі.

Якщо в оцінковому рядку останньої симплексної таблиці оцінка F_j – с _j = 0 відповідає вільній (небазисній) змінній, то це означає, що задача лінійного програмування має альтернативний оптимальний план. Отримати його можна, вибираючи розв’язувальний елемент у зазначеному стовпчику таблиці та здійснивши один крок (одну ітерацію) симплекс-методом. У результаті отримаємо новий опор­ний план, якому відповідає те саме значення функціонала, що і для попереднього плану, тобто функціонал досягає максимального значення в двох точках багатогранника розв’язків, а отже, за властивістю 2 (§ 2.5) розв’язків задачі лінійного програмування така задача має нескінченну множину оптимальних планів.

Таблиця 2.7

ДРУГА СИМПЛЕКСНА ТАБЛИЦЯ ДЛЯ ВІДШУКАННЯ
ОПОРНОГО (ОПТИМАЛЬНОГО) ПЛАНУ

і

Базис

Сбаз

План

c 1

c 2

…

cl

…

cm

cm + 1

…

cj

…

ck

…

cn

θ і

x 1

x 2

…

xl

…

xm

xm + 1

…

xj

…

xk

…

xn

x 1

c 1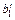

…

…

…

…

…

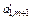
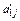
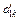
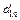
θ1

x 2

c 2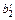

…

…

…

…

…

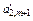
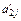
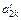
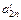
θ2

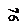M

M

M

M

M

M

M

M

M

M

M

M

M

M

M

M

M

M

l

xl

cl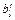

…

…

…

…

…

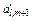
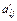
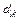
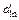
θ l

M

M

M

M

M

M

M

M

M

M

M

M

M

M

M

M

M

M

m

xm

cm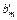

…

…

…

…

…

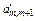
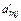
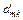
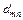
θ m

m + 1

Fj – cj ≥ 0

F (X 1)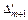

…

…

…

…

…

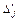
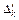
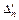
Розв’язання задачі лінійного програмування на відшукання мінімального значення функціонала відрізняється лише умовою оптимальності опорного плану. До базису включають вектор, для якого 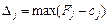, де максимум знаходять для тих j, яким відповідають 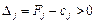. Всі інші процедури симплексного методу здійснюються аналогічно, як у задачі лінійного програмування на відшукання максимального значення функціонала.

2.8.5. Приклад розв’язування
задачі симплекс-методом

Розглянемо застосування симплекс-методу для розв’язання деяких задач лінійного програмування.

Продукція чотирьох видів А, В, С і D прохо­дить послідовну обробку на двох верстатах. Тривалість обробки одиниці продукції кожного виду наведена в табл. 2.8.

Таблиця 2.8

Дата добавления: 2015-05-23