
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Замовлення на рулони паперу
|
|
|
|
| Замовлення | Потрібна ширина рулона, м | Кількість замовлених рулонів |
| 0,8 | ||
| 1,0 | ||
| 1,2 |
Необхідно визначити оптимальний варіант розкрою стандартних рулонів, за якого спеціальні замовлення, що надходять, задовольняють повністю з мінімальними відходами паперу.
Розв’язання. Аби виконати спеціальні замовлення, які надійшли, розглянемо п’ять можливих варіантів розрізування стандартних рулонів, що можуть використовуватися в різних комбінаціях. Варіанти розкрою наведено в табл. 2.10.
Таблиця 2.10
МОЖЛИВІ ВАРІАНТИ РОЗРІЗУВАННЯ СТАНДАРТНИХ
РУЛОНІВ ПАПЕРУ
| Потрібна ширина рулона, м | Кількість нестандартних рулонів за варіантами | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 0,8 | |||||
| 1,0 | |||||
| 1,2 | |||||
| Обсяг відходів, м | 0,4 | 0,2 | 0,8 |
Нехай xj — кількість стандартних рулонів паперу, які буде розрізано j -способом, 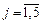 .
.
Обмеження задачі пов’язані з обов’язковою вимогою повного забезпечення необхідної кількості нестандартних рулонів за спеціальними замовленнями. Якщо брати до уваги всі подані в таблиці способи розкрою, то дістанемо такі умови (обмеження) даної задачі:
1. Щодо кількості рулонів шириною 0,8 м:
2 х 1 + х 2 + х 3 = 150.
2. Щодо кількості рулонів шириною 1 м:
х 3 + 2 х 4 = 200.
3. Стосовно кількості рулонів шириною 1,2 м:
х 2 + х 5 = 300.
Цільова функція задачі — це мінімальні загальні втрати паперу під час розрізування стандартних рулонів на рулони нестандартної ширини. Математично вона має такий вигляд:
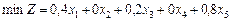 .
.
Математична модель задачі загалом записується так:
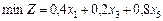
за умов:
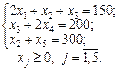
Для розв’язування цієї задачі застосуємо алгоритм симплекс-методу. Оскільки задачу сформульовано в канонічній формі, запишемо її відразу у векторній формі:
|
|
|
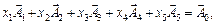
де
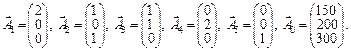
У системі векторів маємо лише один одиничний вектор 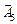 . Тому в перше та друге обмеження введемо штучні змінні х 6 та х 7. Розширена задача матиме вигляд:
. Тому в перше та друге обмеження введемо штучні змінні х 6 та х 7. Розширена задача матиме вигляд:
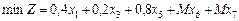
за умов:
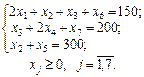
Процес розв’язання задачі симплекс-методом подано у вигляді таблиці:
| Базис | С баз | План | 0,4 | 0,2 | 0,8 | М | M | ||
| х 1 | х 2 | х 3 | х 4 | х 5 | х 6 | х 7 | |||
| х 6 | M | ||||||||
  х 7 х 7
| M | ||||||||
| х 5 | 0,8 | ||||||||
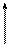 Zj – с j ³ 0 Zj – с j ³ 0
| –0,4 | 0,8 | –0,2 | ||||||
| 350 M | 2 M | M | 2 M | 2 M | |||||
  х 6 х 6
| M | ||||||||
| х 4 | 1/2 | ||||||||
 х 5 х 5
| 0,8 | ||||||||
| Zj – с j ³ 0 | –0,4 | 0,8 | –0,2 | ||||||
| 150 M | 2 M | M | M | ||||||
 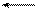 х 1 х 1
| 0,4 | 1/2 | 1/2 | ||||||
| х 4 | 1/2 | ||||||||
| х 5 | 0,8 | ||||||||
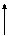 Zj – с j ³ 0 Zj – с j ³ 0
| |||||||||
| х 2 | |||||||||
| х 4 | 1/2 | ||||||||
| х 5 | 0,8 | –2 | –1 | ||||||
| Zj – с j ³ 0 | –2 | –1 |
Згідно з останньою симплексною таблицею запишемо оптимальний план задачі:
Х * = (0; 150; 0; 100; 150),
min Z = 120.
Визначений оптимальний план передбачає: щоб у повному обсязі виконати спеціальні замовлення, які надходять на паперову фабрику, необхідно розрізати 150 стандартних рулонів другим способом, 100 рулонів — четвертим і 150 — п’ятим. За такого оптимального варіанта розкрою обсяг відходів паперу буде найменшим і становитиме 120 м.
2.8.7. Зациклення в задачах
лінійного програмування*
Як доведено вище, оптимальний план задачі лінійного програмування може знаходитись в одній з кутових точок багатогранника розв’язків, кількість яких є скінченною, тому, використовуючи для розв’язування задачі симплексний метод, за скінченну кількість кроків можна знайти оптимальний план або з’ясувати, що задача не має розв’язку. Однак строга монотонність симплексного алгоритму має місце лише у разі невиродженості всіх опорних планів, які отримані в ході ітераційної процедури алгоритму.
|
|
|
Якщо при дослідженні значень 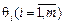 у симплексній таблиці існує кілька однакових значень з-поміж
у симплексній таблиці існує кілька однакових значень з-поміж 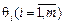 , то це означає, що можна вибрати для виключення з базису більш ніж один вектор. Наступна ітерація симплексного методу призведе до виродженого опорного плану, в якому хоча б одна з базисних змінних дорівнюватиме нулю.
, то це означає, що можна вибрати для виключення з базису більш ніж один вектор. Наступна ітерація симплексного методу призведе до виродженого опорного плану, в якому хоча б одна з базисних змінних дорівнюватиме нулю.
Якщо деякий опорний план буде виродженим, тобто один або більше вільних членів основної системи обмежень дорівнюватимуть нулю, то при визначенні вектора, який необхідно на наступному кроці виводити з базису, найменше значення q буде дорівнювати нулю і відповідати тому рівнянню, вільний член якого нульовий. Отже, в наступній ітерації буде виведена з базису відповідна змінна, причому всі значення базисних змінних в наступному опорному плані залишаться без змін, тобто значення цільової функції після проведення ітерації не зміниться.
Це означає, що наступні ітерації можуть не привести до покращення значення цільової функції. В такому разі після певного числа ітерацій дістають план, який вже було отримано раніше в процесі розв’язування задачі. Подальші ітерації, проведені аналогічно, приведуть до повторного перебору тих самих опорних планів. Вироджений план є причиною того, що теоретично виникає можливість нескінченного числа повторень однакових послідовностей ітерацій, які не покращують розв’язку, тобто обчислювальна процедура не буде мати кінця. Таку ситуацію називають зацикленням. Циклу можна було б уникнути, запам’ятовуючи опорні плани, що утворили цикл, і не повертаючись до них. Проте, щоб забезпечити однозначність вибору вектора, який виводиться з базису, розроблено ряд спеціальних прийомів. Найцікавішим з них є так званий e - метод.
Виродженому плану відповідає вершина множини планів, що утворена більш ніж n гіперплощинами. Інакше кажучи, одна вершина відповідає кільком виродженим планам, що означає злиття кількох вершин багатогранника в одну. Ідея e- методу усунення зациклення полягає в роз’єднуванні злитих вершин. Для цього досить, очевидно, ввести замість нулів у відповідні рівняння якісь інші значення, однак зробити це так, щоб не було знову кількох мінімальних співвідношень у наступному кроці. У такий спосіб замість початкової матимемо змінену задачу. Проте можна легко довести, що, діставши оптимальний план зміненої задачі, й допустивши, що введені величини дорівнюють нулю, матимемо оптимальний розв’язок початкової задачі.
|
|
|
На практиці вводять величини, які є дуже малими – це поліноми довільно взятої малої (близької до нуля) додатної величини e. Коефіцієнтами поліномів беруть коефіцієнти при невідомих (базисних і небазисних) відповідного рівняння, а степенями e -номери цих невідомих, тобто для деякого i -го рівняння маємо поліном виду:
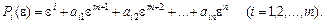
Цілком зрозуміло, що для будь-яких 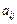 можна вибрати e настільки малим, що завжди
можна вибрати e настільки малим, що завжди 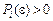 , бо доданки зі степенями e, вищими від і- го, будуть вищого порядку малості у порівнянні з першим
, бо доданки зі степенями e, вищими від і- го, будуть вищого порядку малості у порівнянні з першим  . Внаслідок цього всі утворені поліноми різнитимуться за величиною. В оптимальному плані необхідно буде допустити, що
. Внаслідок цього всі утворені поліноми різнитимуться за величиною. В оптимальному плані необхідно буде допустити, що 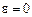 .
.
Зауважимо, що в разі підозри на можливість зациклення (випадок, коли початковий опорний план вироджений) поліноми 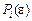 можна одразу додати до вільних членів системи обмежень, внаслідок чого матимемо:
можна одразу додати до вільних членів системи обмежень, внаслідок чого матимемо: 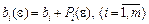 .
.
2.8.8. Геометрична інтерпретація
симплексного методу
Геометричну інтерпретацію симплексного методу можна подати двома різними способами. В одному разі ілюструється зміна базису, яка здійснюється вибором векторів, які включаються до базису та виключаються з нього. В другому, простішому та наочному випадку, процес симплексного методу інтерпретується як послідовний рух через сусідні кутові точки багатогранника розв’язків, що пов’язано зі збільшенням (зменшенням) значення цільової функції.
Дві кутові точки назвемо сусідніми, якщо вони розташовані на одному ребрі багатогранника.
Допустимо, що розглядається задача на відшукання максимального значення лінійної функції 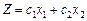 і маємо певний багатокутник її розв’язків (рис. 2.18).
і маємо певний багатокутник її розв’язків (рис. 2.18).
|
|
|
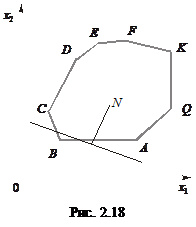 Допустимо, що початковий опорний план відповідає кутовій точці А. Тоді наступний крок симплексного методу приведе до точки Q, (
Допустимо, що початковий опорний план відповідає кутовій точці А. Тоді наступний крок симплексного методу приведе до точки Q, (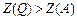 ), а в результаті ще однієї ітерації — до точки K, де лінійна функція набуває максимального значення. Проте, якщо початковим опорним планом буде точка В, то включення вектора до базису за критерієм
), а в результаті ще однієї ітерації — до точки K, де лінійна функція набуває максимального значення. Проте, якщо початковим опорним планом буде точка В, то включення вектора до базису за критерієм 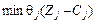 приводить до того, що пряма
приводить до того, що пряма 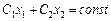 проходитиме через точку С і алгоритм симплексного методу приведе до точок С, D, E, F, K, тобто для отримання оптимального плану необхідно буде виконати ще чотири ітерації.
проходитиме через точку С і алгоритм симплексного методу приведе до точок С, D, E, F, K, тобто для отримання оптимального плану необхідно буде виконати ще чотири ітерації.
Отже, очевидно, що застосування симплексного методу не дає змоги одразу перейти від опорного плану (точки В) до оптимального (точки К). Фактично розв’язок отримують, рухаючись вздовж межі (ребер) простору розв’язків, причому не завжди такий шлях буде найкоротшим. Кількість ітерацій за реалізації симплексного алгоритму визначається вибором початкового опорного плану та кількістю кутових точок, що траплятимуться на шляху прямої 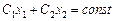 .
.
2.9. Модифікації симплексного методу*
Симплексний метод є ефективною, досить простою процедурою, проте не позбавленою деяких недоліків. Цей факт пояснює численні спроби модифікування симплексного методу, які можна зустріти в літературі, наприклад [31].
Хоча теоретична основа симплексного методу гарантує збіжність до оптимального розв’язку за скінченну кількість кроків, але труднощі обчислювального характеру, що виникають внаслідок помилок округлення в процесі машинних розрахунків, у цьому методі не враховані. Такі проблеми зустрічаються передусім тоді, коли штучні змінні є частиною початкового базисного розв’язку. Використання як ± М у цільовій функції дуже великих чисел може призвести до помилки округлення, що зумовлена операціями над групою чисел, яка містить як дуже великі, так і відносно малі числа. Розглянемо задачу (2.60)—(2.61).
Зазначена загроза зменшується розбиттям процесу розв’язування задачі на два етапи. На першому етапі розв’язується задача виду:
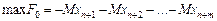
за обмежень:
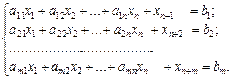
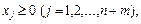
де 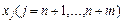 – штучні змінні.
– штучні змінні.
Очевидно значення цільової функції для оптимального плану буде 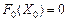 . Отже, при
. Отже, при 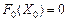 початкова задача має допустимий базисний розв’язок, причому такий, що не містить штучних змінних. На другому етапі розв’язування задачі як початковий опорний план береться Х0, і процес продовжується за звичайним алгоритмом симплексного методу. Завдяки поділу розв’язування задачі на два етапи на кожному з них у процесі обчислень використовуються майже однакові за значеннями числа. Перший етап характеризується використанням лише великих чисел як коефіцієнтів цільової функції, проте на другому етапі задача не містить штучних змінних, отже, значення, що відповідають ± М,не розглядаються.
початкова задача має допустимий базисний розв’язок, причому такий, що не містить штучних змінних. На другому етапі розв’язування задачі як початковий опорний план береться Х0, і процес продовжується за звичайним алгоритмом симплексного методу. Завдяки поділу розв’язування задачі на два етапи на кожному з них у процесі обчислень використовуються майже однакові за значеннями числа. Перший етап характеризується використанням лише великих чисел як коефіцієнтів цільової функції, проте на другому етапі задача не містить штучних змінних, отже, значення, що відповідають ± М,не розглядаються.
Крім того, якщо на першому етапі розв’язання задачі 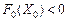 , то це означає, що деякі зі штучних змінних додатні, тобто допустимих планів для початкової задачі не існує, її система обмежень несумісна, задача розв’язків не має. Отже, немає потреби переходити до другого етапу.
, то це означає, що деякі зі штучних змінних додатні, тобто допустимих планів для початкової задачі не існує, її система обмежень несумісна, задача розв’язків не має. Отже, немає потреби переходити до другого етапу.
Двохетапний метод застосовують до задач, що вимагають операцій над дуже великими числами, які входять у цільову функцію. Однак навіть за умови, що така ситуація не склалася, тобто задача не містить штучних змінних, проблеми обчислювального характеру залишаються. Застосування методу виключення змінних Жордана—Гаусса для отримання послідовного ряду симплексних таблиць призводить до накопичення і поширення помилок округлення в такій мірі, що вони спотворюють початкові дані задачі. Розглянемо приклад, в якому помилки округлення пов’язані з визначенням умов допустимості розв’язку. Допустимо, що точне значення деякої базисної змінної 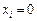 , вибрано деякий напрямний вектор
, вибрано деякий напрямний вектор 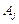 і в цьому векторі єдина невід’ємна компонента, що відповідає і -ій (нульовій) базисній змінній, також дорівнює нулю. Тоді вектор
і в цьому векторі єдина невід’ємна компонента, що відповідає і -ій (нульовій) базисній змінній, також дорівнює нулю. Тоді вектор 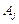 вводити до базису не можна. Однак, унаслідок помилки округлення можлива ситуація, коли розраховане значення базисного вектора
вводити до базису не можна. Однак, унаслідок помилки округлення можлива ситуація, коли розраховане значення базисного вектора 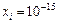 , а значення коефіцієнта, що відповідає і -ій базисній змінній та j -му вектору в симплексній таблиці —
, а значення коефіцієнта, що відповідає і -ій базисній змінній та j -му вектору в симплексній таблиці — 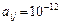 . Тоді вектор
. Тоді вектор 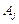 буде вибрано для введення до базису.
буде вибрано для введення до базису.
З метою зменшення впливу помилок округлення був розроблений модифікований симплексний метод. Основні етапи його алгоритму по суті такі ж, як і для симплексного методу. Головна відмінність полягає в тому, що для отримання послідовності симплексних таблиць у модифікованому симплексному методі не застосовується метод виключення змінних Жордана—Гаусса. Допустимо, що розглядається задача лінійного програмування, де базис утворюють останні n + m векторів, які позначимо через Х 2, а відповідні їм коефіцієнти цільової функції — через С 2.Аналогічно перші n змінних позначимо через Х 1, а відповідні коефіцієнти цільової функції — через С 1. Коефіцієнти векторів Х 1 у системі обмежень утворюють матрицю А. Тоді схематично першу та останню симплексні таблиці можна подати у вигляді (табл. 2.11):
Таблиця 2.11
| Базис | План | C1 | C 2 |
| Х 1 | Х 2 | ||
| Х 2 | b | A | E |
| Δj | C 2 X 2 | C 2 A – C 1 | |
| .................................................................................................. | |||
| XВ | b | B-1A | B-1 |
| Δj | CB B-1b | CB B- 1 A – C 1 | CB B- 1 A – C 2 |
де В– 1 — матриця, обернена до одиничної, з першої симплексної таблиці. Як видно з наведеної табл. 2.11, вся симплексна таблиця сформована шляхом використання початкових даних (матриця А) та обернення поточного базису В- 1. Отже, в обчислювальних процедурах модифікованого симплексного методу головна увага зосереджена на мінімізації помилок округлення при обчисленні матриці В– 1.
Крім зменшення помилок округлення, модифікований симплексний метод уможливлює також зменшення тривалості розрахунків. Зокрема, якщо в матриці обмежень А відносна кількість нульових елементів велика, то модифікованим симплексним методом можна скористатись для зменшення кількості операцій множення (порівняно зі звичайним симплексним методом, у якому елементи таблиці, особливо нульові, в процесі послідовних операцій постійно змінюються). Взагалі відомо, що потрібний для реалізації модифікованого симплексного методу обсяг обчислень тим менший, чим менша щільність матриці А (щільність — це відношення кількості ненульових елементів до загальної кількості елементів матриці) та відношення кількості обмежень до кількості змінних.
 Заключні зауваження
Заключні зауваження
У цьому розділі розглянуто два методи (графічний і симплекс-метод) розв’язання задач лінійного програмування. Графічний метод для розв’язування реальних задач не придатний, оскільки економіко-математична модель для його застосування мусить мати тільки дві змінні (види діяльності). На практиці такі задачі не виникають. Якщо економіко-математична модель адекватно описує реальні технологічні та економічні процеси, то вона, як правило, має сотні чи навіть тисячі змінних і обмежень. Для розв’язування таких задач використовується симплексний метод, із застосуванням якого теоретично можна дістати оптимальний розв’язок довільної лінійної економіко-математичної задачі.
Графічний метод є важливим для осмислення сутності оптимізації, геометричної інтерпретації постановки та розв’язку задач лінійного програмування.
Слід підкреслити, що економічні процеси є нелінійними, стохастичними, динамічними тощо. Далі будуть описані відповідні методи розв’язання таких задач. Проте звертаємо увагу читача на те, що є багато технологічних та економічних процесів, які з достатньою для практики точністю можна описати лінійними залежностями, тобто такі моделі є лінійними, а отже, для знаходження їх оптимального розв’язку застосовується симплексний метод.
Для поглибленого вивчення методів оптимізації лінійних задач можна скористатися літературними джерелами [6; 9; 12; 19; 26; 28].
 Контрольні запитання
Контрольні запитання
1. Запишіть загальну математичну модель задачі лінійного програмування.
2. Як звести задачу лінійного програмування до канонічної форми?
3. Які є форми запису задач лінійного програмування?
4. Поясніть геометричну інтерпретацію задачі лінійного програмування.
5. Який розв’язок задачі лінійного програмування називається допустимим?
6. Поясніть, що називається областю допустимих планів.
7. Який план називається опорним?
8. Який опорний план називається невиродженим?
9. Сформулюйте основні аналітичні властивості розв’язків задачі лінійного програмування.
10. Які задачі лінійного програмування можна розв’язувати графічним методом?
11. За яких умов задача лінійного програмування з необмеженою областю допустимих планів має розв’язок?
12. Суть алгоритму графічного методу розв’язання задач лінійного програмування.
13. Для розв’язування яких математичних задач застосовується симплексний метод?
14. Суть алгоритму симплексного методу.
15. Сформулюйте умови оптимальності розв’язку задачі симплексним методом.
16. Як вибрати спрямовуючий вектор-стовпець?
17. Як вибрати розв’язувальний елемент?
18. Суть методу Жордана—Гаусса.
19. Суть методу штучного базису.
 Приклади та завдання
Приклади та завдання
для самостійної роботи
Розв’язати графічним методом такі задачі.
Задача 2.1. Комерційна фірма рекламує свою продукцію, використовуючи місцеві радіо- та телевізійну мережі. Витрати на рекламу в бюджеті фірми становлять 10 000 грн на місяць. Одна хвилина радіореклами коштує фірмі 5 грн, а телереклами — 90 грн. Фірма має намір використовувати радіорекламу принаймні вдвічі частіше, ніж рекламу на телебаченні. Досвід свідчить, що обсяг збуту, який забезпечує 1 хв телереклами, у 30 разів перевищує обсяг збуту, що забезпечує 1 хв радіореклами.
Визначити оптимальний розподіл коштів, які щомісяця мають витрачатися на рекламу, за якого обсяг збуту продукції фірми був би найбільшим.
Задача 2.2. Невелике сільськогосподарське підприємство спеціалізується на вирощуванні овочів, зокрема капусти та томатів, використовуючи для підвищення їх урожайності мінеральні добрива (фосфорні та калійні). Норми внесення мінеральних добрив під кожну культуру та їх запаси у господарстві наведені в таблиці:
Таблиця 2.7
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 709; Нарушение авторских прав?; Мы поможем в написании вашей работы!