Структурный автомат

2.1. Канонический метод структурного синтеза автоматов
2.1.1. Композиция элементарных автоматов
2.1.2. Структурный алфавит и автоматное время
2.1.3. Соотношение абстрактного и структурного автоматов
2.1.4. Основы канонического синтеза автоматов
2.1.5. Ограничения в работе схем
2.1.6. Пример полного автомата Мура
2.1.7. Представление структурного автомата
2.1.8. Работа автомата
2.1.9. Синтез комбинационных схем
2.1.10. Абстрактный и структурный автомат памяти
2.1.11. Пример функционирования автомата памяти
2.2. Пример канонического метода структурного синтеза
2.2.1. Таблицы и графы абстрактного структурного автомата (С-А) и автомата памяти (АП)
2.2.2. Кодирование сигналов и состояний
2.2.3. Структура и таблицы синтезированного автомата
2.2.4. Функции выходов комбинационных схем КС1 и КС2
2.2.5. Функции возбуждения памяти
2.2.6. Построение логической схемы структурного автомата
2.2.7. Минимизация комбинационных схем
2.3. Синтез автоматов на элементах задержки, триггерах со счетным и раздельным входами
2.3.1. Синтез на элементах задержки
2.3.2. Синтез на триггерах со счетным входом
2.3.3. Синтех на триггерах с раздельными входами
2.4. Графический метод структурного синтеза автомата
2.4.1. Графический синтез автомата на элементах задержки
2.4.2. Графический синтез автомата на триггерах со счетным входом
2.4.3. Графический синтез автомата на триггерах с раздельным входом

2.1. Канонический метод структурного синтеза автоматов

2.1.1. Композиция элементарных автоматов

Вслед за этапом абстрактного синтеза автоматов, заканчивающимся минимизацией числа состояний, следует этап структурного синтеза, целью которого является построение схемы, реализующий автомат из логических элементов заданного типа. Если абстрактный автомат был лишь математической моделью дискретной системы, то в структурном автомате учитывается структура входных и выходных сигналов автомата, а также его внутреннее устройство на уровне структурных схем. Структурным синтезом занимается структурная теория автоматов, основной задачей которой является нахождение общих приемов построения структурных схем на основе композиции элементарных автоматов, принадлежащих к заранее заданному конечному числу типов. Под композицией элементарных автоматов [7] в общем случае понимается следующее.

Пусть заданы элементарные автоматы S1,:, Sk. Произведем объединение элементарных автоматов в систему совместно работающих автоматов. Введем в рассмотрение некоторое конечное множество узлов, называемых внешими выходными узлами. Эти узлы отличаются от узлов рассматриваемых элементарных автоматов, которые носят название внутренних. Композиция автомата состоит в том, что в полученной системе элементарных автоматов S1,:, Sk и внешних узлов производится отождествление некоторых узлов (как внешних так и внутренних). С точки зрения совместной работы системы автоматов смысл операции отождествления узлов состоит в том, что элементарный сигнал, попадающий на один из узлов, входящих в множество отождествляемых между собой узлов, попадает тем самым на все узлы этого множества. После проведенных отождествлений узлов система автоматов превращается в так называемую схему (сеть) автоматов. Будем считать, что автоматы, входящие в систему автоматов, работают совместно, если в каждый момент автоматного времени на все внешние входные узлы подается набор входных сигналов (структурный входной сигнал схемы) и со всех внешних выходных узлов снимается набор выходных сигналов (структурный выходной сигнал). Следует заметить, что при построении схемы автоматов должны выполняться условия корректности [7].

2.1.2. Структурный алфавит и автоматное время

Набор возможных значений сигналов, подаваемый на один внешний вход (входной) узел, называется структурным входным (выходным) алфавитом автомата. Предполагается, что все входящие в компазицию автоматы имеют один и тот же структурный алфавит и работают в одном и том же автоматном времени. В настоящее время наиболее распрастраненным структурным алфавитом является двоичный, что объясняется простотой его представления в современных элементах и приборах. Кроме того, для двоичного алфавита наиболее разработан аппарат булевых функций, позволюящий производить многие операции над схемой формально. Поэтому в дальнейшем при решении задач структурного синтеза автоматов будет использоваться в основном двоичный структурный алфавит.

2.1.3. Соотношение абстрактного и структурного автоматов

Абстрактный автомат:

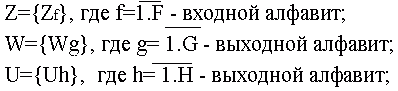
Структурный автомат:

Предположим, что в каждый момент автоматного времени структурный выходной сигнал схемы однозначно определяется поступившей к этому времени конечной последовательностью структурных входных сигналов, начальными состояниями входящих в схему автоматов и сделанными при построении схемы отождествлениями узлов. В этом случае построенную схему будем рассматривать как некоторый автомат S, а саму схему назовем структурной схемой этого автомата. Построенный таким образом автомат S есть результат комразиции элементарных автоматов S1,:, Sk.

В отличие от абстрактного С -автомата, имеющего один входной и два выходных канала, на которые поступают сигналы во входном Z={z₁,...,z_f,...,z_F} и выходных W={w₁,...,w_g...,w_G}, U={u₁,...,u_h...,u_H} алфавитах автомата, структурный автомат имеет входные X₁,..., X_i..., X_I и выходные Y₁,..., Y_n..., Y_N; r₁,..., r_d..., r_D; каналы, на которых появляются сигналы в структурном алфавите автомата.
В случае двоичного алфавита каждый выходной Z1 и выходные Wg и Uh сигналы абстрактного автомата могут быть закодированы векторами длины L, N и D соответственно, компоненты которых принимают два значения- нуль и единицу:

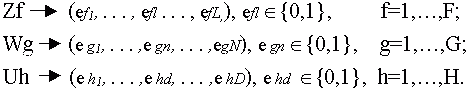
Очевидно, что L>= ]log₂F[ N>= ]log₂ G[ D>= ]log₂H[, где ]a[ означает ближайшее число, большее а или равное ему, если а - целое.

2.1.4. Основы канонического синтеза автоматов

На этапе структурного синтеза предварительно выбираются элементарные автоматы, из которых путем их композиции строится структурная схема полученного на этапе абстрактного синтеза автомата Мили, Мура или С -автомата. Если решение задачи структурного синтеза существует, говорят, что заданная система автоматов структурно полна. Как отмечалось в [7], в настоящее время нет сколько-нибудь эффективных методов (существенно боле простых, чем метод перебора всех вариантов) решения основной задачи структурного синтеза при любом наборе структурно полных систем элементарных автоматов. Поэтому обычно применяется так называемый канонический метод структурного синтеза, при котором используются элементарные автоматы некоторого специального вида: 1) автоматы с памятью, имеющие более одного состояния, и 2) автоматы без памяти- с одним состоянием. Автоматы первого класса носят название элементов памяти, а автоматы второго класса - комбинационных или логических элементов. Теоретическим обоснованием канонического метода структурного синтеза является доказанная в [7] теорема о структурной полноте.

Теорема: Всякая система элементарных автоматов, которая содержит автомат Мура с нетривиальной памятью, обладающий полной системой переходов и полной системой выходов, и какую -либо функционально полную систему логических элементов, является структурно полной.

Существует общий конструктивный прием (канонический метод структурного синтеза), позволяющий в рассматриваемом случае свести задачу структурного синтеза произвольных автоматов к задаче синтеза комбинационных схем.

Результатом канонического метода структурного синтеза является система синтеза логических уравнений, выражающая зависимость выходных сигналов автомата и сигналов, подаваемых на входы запоминающих элементов, от сигналов приходящих на вход всего автомата в целом, и сигналов, снимаемых с выхода элементов памяти. Эти уравнения называютя каноническими.

2.1.5. Ограничения в работе схем

Для правильной работы схем, очевидно нельзя разрешать, чтобы сигналы на входе запоминающих элементов непосредственно участвовали в образовании выходных сигналов, которые по цепям обратной связи подавались бы в тот же самый момент времени на эти выходы. В связи с этим запоминающими элементами должны быть на автоматы Мили, а автоматы Мура (см. уравнения функционирования этих автоматов в параграфе 1-1).
Таким образом, структурно полная система автоматов должна содержать хотя бы один автомат Мура. В то же время для синтеза любых автоматов с минимальным числом элементов памяти необходимо в качестве таких элементов выбрать автоматы Мура, имеющие полную систему переходов в полную систему выходов- так называемые полные автоматы.

2.1.6. Пример полного автомата Мура

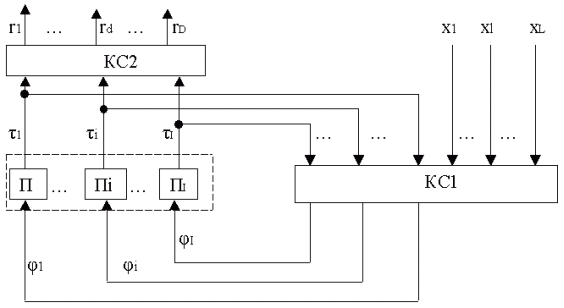
Рассмотрим полноту автоматов памяти на примере автомата Мура П_i у которого Q={q₁, q₂, q₃}; W={w₁, w₂, w₃}; B={b₁, b₂, b₃} -алфавиты входной, и выходной и состояний, а функции переходов и выходов заданы отмеченной таблицей переходов (табл. 2-1).

T2-1. Отмеченная таблица переходов полного автомата Мура b= (b,q) w= (b)

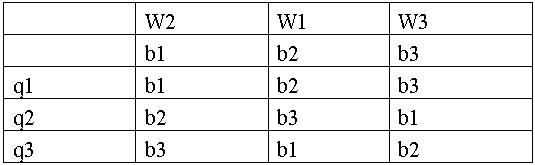
Полнота системы переходов означает, что для любой пары состояний (b_m, b_s) автомата найдется входной сигнал, переводящий первый элемент этой пары (b_m) во второй (b_s), т.е. в таком автомате в каждом столбце таблицы переходов должны встречаться все состояния автомата. Полнота системы выходов автомата Мура состоит в том, что каждому состоянию автомата поставлен в соответствие свой особый выходной сигнал, отличный от выходных сигналов других состояний. Очевидно, что в таком автомате число выходных сигналов равно числу состояний автомата. Вместе с предыдущим утверждением это приводит к тому, что в автомате Мура с полной системой выходов можно отождествить состояние автомата с его входными сигналами. В связи с этим в автоматах памяти мы будем использовать одни и те же обозначения и для состояний, и для выходных сигналов, т.е. отмеченная таблица переходов в автоматах Мура с полной системой выходов превращается просто в таблицу переходов. Автомат Мура в таб. 2-1 удовлетворяет условиям полноты системы переходов и выходов. В связи с этим в качестве его входного алфавита можно принять алфавит B={b₁, b₂, b₃}.

2.1.7. Представление структурного автомата

Канонический метод структурного синтеза предполагает представление структурной схемы С -автомата в виде трех частей: памяти и двух комбинационных систем KC1 и KC2 (рис.2-1). Поясним назначение каждой из них.

Память автомата состоит из предварительно выбранных атоматов памяти Мура П₁,:, П_i,:, П_I. После выбора элементов памяти каждое состояние am(m=1,:,M) абстрактно С -автомата представляется (кодируется) в структурном автомате векторм (e_m1,...,e_mi,...,e_mI), компонентами которого являются состояния элементов памяти П_i(i=1,:, I) Если все автоматы П₁,:,П _I одинаковы, то их число I? log_oM, где O - число состояний элементарного автомата памяти.

A)

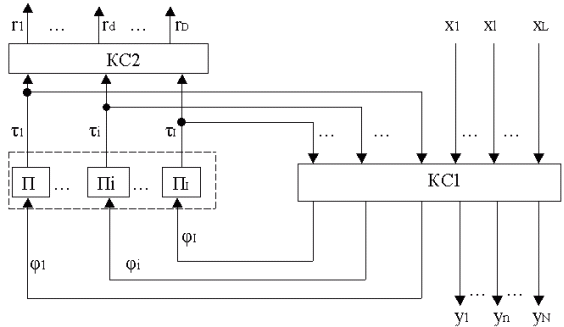
Рис. 2-1.Представление С-автомата в виде памяти и двух комбинационных схем.

Функции:

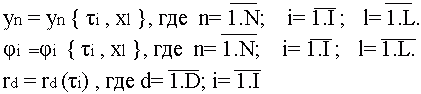
Б)

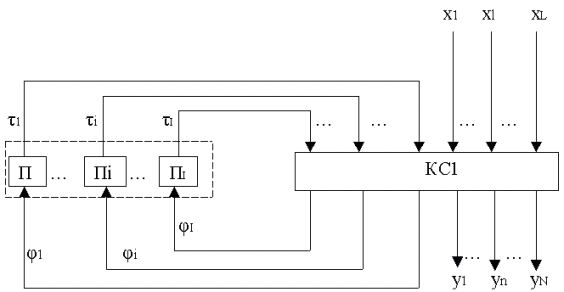
Представление автомата Мили в виде памяти и двух комбинационных схем.

В)

Представление автомата Мура в виде памяти и двух комбинационных схем.

2.1.8. Работа автомата

Переходу абстрактного С -автомата из состояния а_m в состояние а_s под действием входного сигнала z_f c выдачей выходного сигнала w_g соответствует переход структурного автомата из состояния (e_m1,..., e_mI) в состояние (e_s1,...,e_sI) под действием входного сигнала (ef1,..., efL,) с выдачей выходного сигнала (e_g1,...,e_gN) типа 1. Изменение состояний элементов памяти на таком переходе происходит под действием сигналов на входах памяти автомата = ( ₁,:, _i,:, _I), снимаемых с выхода KC1. После перехода в состояние a_s [ или в структурном автомате - в состояние (e_s1,...,e_sI) ] автомат выдает выходной сигнал типа 2 u_h = (e_h1,...,e_hD) все время, пока он находится в таком состоянии. Комбинационная схема KC1 служит для формирования сигналов типа 1 и входных сигналов автоматов памяти, а KC2 - для формирования сигналов типа 2. Структурный синтез рассматривается для С -автомата, поскольку эта модель является обобщением модели Мили и Мура. Если необходимо синтезировать автомат Мили, то можно считать, что в С -автомате не задана функция 2 и отсутствует KC2. В случае модели Мура незаданной оказывается функция 1 и в KC1 нет выходных каналов y₁,:,y _N.

2.1.9. Синтез комбинационных схем

Таким образом, после выбора элементов памяти и кодирования состояний синтез структурного автомата сводится к Синтезу комбинационной схемы, реализующей функции:

где т=(т₁,:, т_I) - функция обратной связи от памяти автомата к комбинированной схеме. Функция = ( ₁,:, _i,:, _I) носит название функции возбуждения памяти автомата.

2.1.10. Абстрактный и структурный автомат памяти

a)

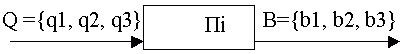
b)

Рис. 2-2. Автомат памяти: a) абстрактный, b) структурный.

Автомат памяти также можно рассматривать на абстрактном и структурном уровнях. Абстрактный автомат памяти П_i,заданный табл. 2-1 имеет один входной и один выходной каналы (рис. 2-2,а).

При переходе от абстрактного к структурному автомату П_i его входные и выходные сигналы должны быть закодированы наборами сигналов на входных и выходных каналах. При двоичном структурном алфавите автомат П_i будет иметь 2 входных 2 выходных канала (рис. 2-2,b). В общем случае, если абстрактный автомат памяти имеет h состояний (B={b₁,:,b_h}) и p входных сигналов (Q={q₁,:,q_p}), то число его входных K и выходных T каналов должно быть K?log_np и T? log_vh, где n и? - число букв в структурных входных и выходных алфавитах автомата памяти П_i. Таким образом, возвращаясь к рис. 2-1, необходимо запомнить, что сами компоненты _i и т_i (i=1,:,I) векторов сигналов возбуждения памяти и сигналов обратной связи от памяти? также могут быть представлены в виде векторов _i =( _i1,:, _iK) т_i = (т_i1,:, т_iT).

2.1.11. Пример функционирования автомата памяти

Как уже отмечалось, мы будем пользоваться, если не оговорено особо, двоичным структурным алфавитом как для входных и выходных каналов синтезируемого автомата, так и для входных и выходных каналов автоматов памяти. Алфавит состояний автоматов памяти также будет в большинстве случаев двоичный, т.е. в качестве элементов памяти в основном будут использоваться автоматы с двумя состояниями.

При построении функции возбуждения памяти автомата будем использовать функцию входов элемента памяти м (b_m, b_s) ставящую в соответствие каждой паре состояний (b_m, b_s) сигнал, который должен быть подан на вход этого автомата для перевода его из состояния b_m в состояние b_s. Функцию входов также удобно задавать в виде таблицы. Для автомата памяти, функция переходов которого приведена в табл. 2-1, функция входов задана табл. 2-2, в которой входной сигнал м (b_m, b_s) стоит во втором столбце между состояниями b_m и b_s. Из табл. 2-2 видно, что для перехода из b₁ в b₂ необходимо подать входной сигнал q₂ а из b₂ в b₃ - входной сигнал q₁ и т.д.

T2-2. Функция входов абстрактного автомата памяти.

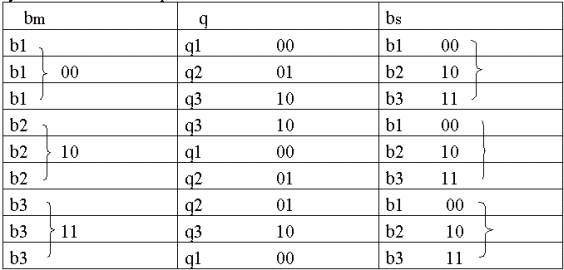
T2-3. Функция входов структурного автомата памяти.

Если входные и выходные сигналы (они же состояния) автомата памяти закодированы наборами ( _i1,:, _iK) и (т_i1,:, т_iT) сигналов на его входных и выходных каналах соответственно, то элементами таблицы, задающей функцию входов, вместо сигналов q₁,:.,q_p, будут соответствующие им наборы. Так, если для нашего примера (табл. 2-2) ввести кодирование

то соответствующая функция входов превратится в табл.2-3, т.е для перехода из состояния (00) в состояние (10) нужно подать нуль на первый входной канал и единицу на второй, а при переходе из (00) в (11) - два нуля на оба входных канала.

2.2. Пример канонического метода структурного синтеза

2.2.1. Таблицы и графы абстрактного структурного автомата (С-А) и автомата памяти (АП)

Частичный С-А зададим таблицей переходов Т-4 и отмеченного таблицей переходов Т-5ю

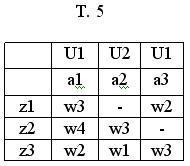
Будем синтезировать С-А, используя в качестве логических элементов логические элементы "НЕ", "ИЛИ", "И" и АП в таблице, переход которых представлен так:

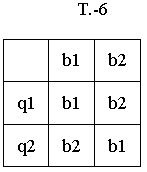
2.2.2. Кодирование сигналов и состояний

Будем все (и структурные входные и выходные алфавиты, и алфавит состояний синтезируемого автомата и алфавит АП) считать двоичными.

Для структурного А-S и АП закодируем все входные и выходные сигналы и состояния.

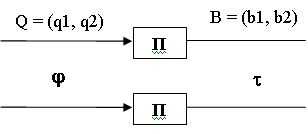
Для АП в абстрактном АП будут 2 входных и 2 выходных сигнала, в структурном будет 1 входной и 1 выходной канал.

Функция выходов и переходов АП будет представлена в таблицах Т-9 и Т-10.

Перейдем к абстрактному А-S. У него 3 состояния, поэтому у структурного А-S будет 2 АП: П₁ и П₂; 3 входных сигнала z₁, z₂, z₃; 4 выходных сигнала 1 рода w₁..w₄ и 2 выходных сигнала 2 рода U₁, U₂ требуют 2 входных (х₁, х₂), 2 выходных (y₁, y₂) 1 рода сигналов и 1 выходной сигнал (r) 2 рода. Результаты кодирования сведем в таблице Т.11-14.

2.2.3. Структура и таблицы синтезируемого автомата

Блок-схема структурного А-S:

В таблице Т-4 и Т-5 заменяем состояния и сигналы их кодами и получаем таблицу переходов структурного автомата и отмеченную таблицу выходов структурного автомата:

Теперь после выбора элементов памяти и кодирования состояний синтез автомата сводится к синтезу КС, которые должны реализовать функции:

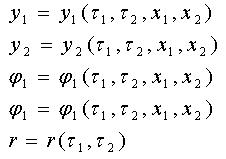
2.2.4. Функции выходов комбинационных схем КС1 и КС2

Функции y₁, y₂ получаются сразу из Т-16, как дизъюнкция конъюнкции тех наборов переменных (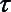 ₁, 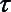₂, x₁, x₂), на которых эти функции принимают значение 1.

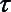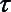По Т-16 находятся функции r = r( ₁, ₂):

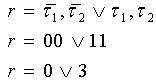
2.2.5. Функции возбуждения памяти

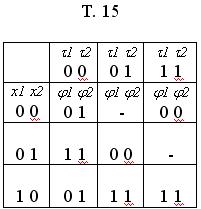
Для определения функции возбуждения памяти ( ₁, ₂) рассмотрим таблицу переходов структурного А-S (Т-15):

Пусть автомат из состояния 01 переходит в состояние 11 под действием входного сигнала 10. Этому переходу соответствуют переходы АП П₁ из состояния 0 в 1 и переходы АП П₂ из состояния 1 в 1.

Переходы АП регулируются функциями входов структурного АП (Т-10).

Для перехода АП из 0 в 1 (П₁) надо на вход подать 1. Для перехода АП П₂ из 1 в 1 надо подать 0.Все переходы по Т-15 с помощью Т-10 сводятся к Т-17.

По Т-17 находим значение функции возбуждения памяти.

2.2.6. Построение логической схемы структурного автомата

Для построения схемы выпишем все функции.

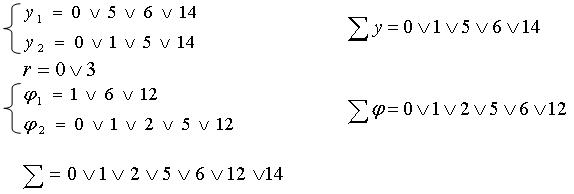
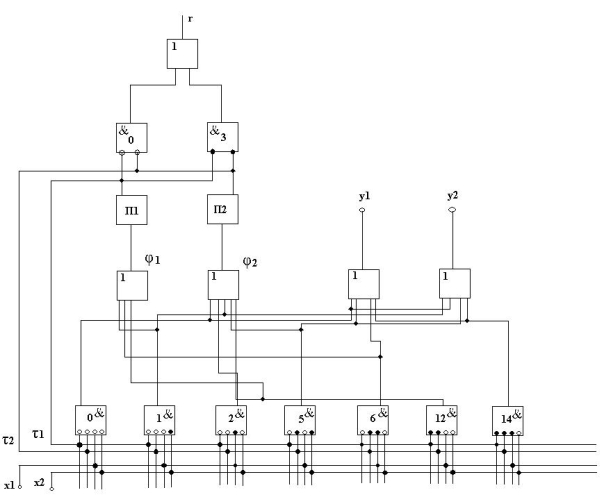
2.2.7. Минимизация комбинационных схем

Для минимизации КС необходимо сократить полученные выражения функций (y, , r). Для этого можно использовать наборы переменных, на которых эти функции не определены.

Правила неопределенности:
1) Если некоторый код

не используется для кодирования состояния автомата, то для всевозможных наборов
,
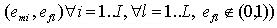полученных из этого кода и всех кодов входных сигналов, все компоненты функции возбуждения памяти и функции выходов 1 типа неопределенны (m - состояние, f - сигнал).

В примере среди кодов состояний Т-11 нет кода 10, следовательно наборы не определены, т.е. они составляют область неопределенности для функций ₁, ₂, y₁, y₂. Также не определены функции r при 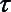₁ = 1, 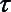₂ = 0.
2) Если некоторый код

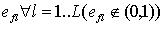
не используется для кодирования входных сигналов, то на всевозможных наборах
,
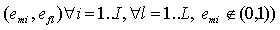полученных из всех кодов состояний и этого кода, все компоненты функции возбуждения памяти и функции выходов 1 типа не определены. В примере среди кодов входных сигналов Т-12 не используется код 11, следовательно, наборы
,
не входят в область определенности функций ₁, ₂, y₁, y₂. Эти наборы не определены.
3) Если на некоторой паре состояний (а_m, a_s) функция переходов не определена, то на наборе
,
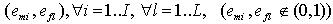все компоненты функции переходов не определены, т.е. прочерки в таблице функции возбуждения совпадают с прочерками в таблице переходов, и из Т-17 имеем 2 таких набора: (0100, 1101).
4) Аналогично 3), если на некоторой паре (a_m, z_s) функция выходов 1 типа не определена, то на наборе, соответствующем этой паре все компоненты функции выходов 1 типа не определены. Из Т.-16 - 2 набора (0100, 1101).

2.3. Синтез автоматов на элементах задержки, триггерах со счетным и раздельным входами

Процесс построения функции возбуждения памяти автомата может быть существенно упрощен. Рассмотрим синтез автомата на задержках триггера со счетным входов и с раздельными входами.

Продолжим пример синтеза автомата, заданного таблицами Т-15-16.

Функции выходов во всех случаях представления АП будут строиться одинаково, так как таблица выходов синтезируемого автомата не зависит от выбора того или иного элемента памяти.

2.3.1. Синтез на элементах задержки

Элемент задержки имеет 1 вход и 1 выход. Его функцией является задерживать поступивший на его вход сигнал на 1 машинных такт.

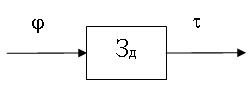
Функция переходов и функция выходов элемента задержки как автомата Т-18, Т-19.

Как видно из Т-19 состояния, в которые переходит элемент задержки полностью совпадает с поступившем на его вход сигналом. Поэтому таблица возбуждения синтезируемого автомата совпадает с Т-15, т.е. вместо 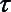₁, 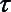₂ будем писать ₁, ₂.

Теперь получаем функции:

2.3.2. Синтез на триггерах со счетным входом

Триггер со счетным входом имеет 1 вход и 1 выход.

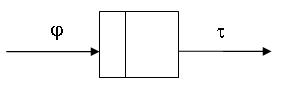
Функция переходов и входов в Т-20-21

Как видно из Т-21 входной сигнал на триггере должен быть равен сумме по модулю 2 кода исходного состояния и переходного состояния.

На основании этого при синтезе автомата на триггерах со счетным входом, таблица функции возбуждения можно получить из таблицы переходов Т-15 так

Элемент таблицы Т-22, стоящий на i-строке и j-столбце равен покомпонентной (поразрядной) сумме по модулю 2 вектора кода состояния, отмечающего j-столбец и вектора кода состояния, стоящего на пересечении i-строки и j-столбца в таблице переходов автомата Т-15, т.е. поразрядной сумме по модулю 2 кодов исходных состояний и состояний переходов.

В примере на 3-строке и 2-столбце будет расположен элемент, полученный сложением по модулю 2 разрядов исходного состояния второго столбца Т-15 и состояния перехода, стоящего в 3-строке и 2-столбце в этой же таблице.

Теперь функции возбуждения получаются просто:

2.3.3. Синтез на триггерах с раздельными входами

Триггер с раздельными входами имеет 2 входа.

- единичный вход;
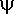- нулевой вход;
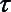- выход.

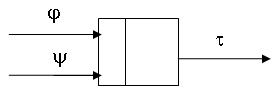
Так как в таких триггерах имеется 2 входных канала, то возможны 4 комбинации входных сигналов. Но в комбинации входных сигналов 11 считается запрещенной. Поэтому таблица переходов этого триггера имеет 3 строки, Т-23.

Из Т-24 при поступлении 1 на любой нулевой канал, триггер переходит в состояние 0 независимо от того, в каком состоянии он находился. При поступлении 1 на единичный вход триггер переходит в состояние 1.

Т-24 можно переписать:

По Т-25 переходу из 0 в 0 соответствует входной сигнал Х0, где Х означает, что переход не зависит от сигнала на нулевом канале. Аналогично для перехода из 1 в 1 - входной сигнал 0Х.

Т-25 дает систему подстановок при переходе от Т-15 к таблице функции возбуждения АП, Т-26.

Пусть в Т-15 переход из состояния 00 в 01 под действием входного сигнала 00 соответствует переходу в структурном автомате двух триггеров Тр₁, Тр₂. Тр₁ переходит из 0 в 0, чему соответствует подстановка Х0 в Т-25. Тр₂ переходит из 0 в 1, подстановка 01 для Тр₂.

Получаем:

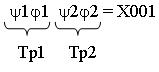
Выписывая из Т-26 наборы переменных 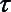₁, 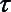₂, x₁, x₂ соответствующие единицам на входах триггеров Тр₁, Тр₂ получим выражения для функции возбуждения памяти автомата.

Все функции, получаемые из Т-26 для элементов, отмеченных х-ом будут неопределенны. Их определение может быть произведено для минимизации или для определения функции возбуждения.

Логическая схема автомата, синтезируемого на элементах И - ИЛИ - НЕ и триггерах с раздельными входами, в соответствии с функциями для выходных сигналов и для функции возбуждения памяти имеет вид:

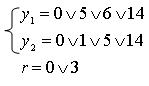
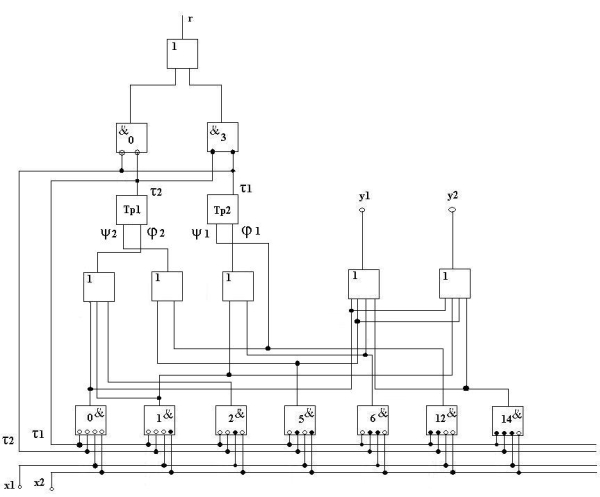
2.4. Графический метод структурного синтеза автомата

2.4.1. Графический синтез автомата на элементах задержки

При графическом методе синтеза структурный С-А представлен в виде графа. Автомат предыдущего примера - Т-4, Т-5 изображается так:

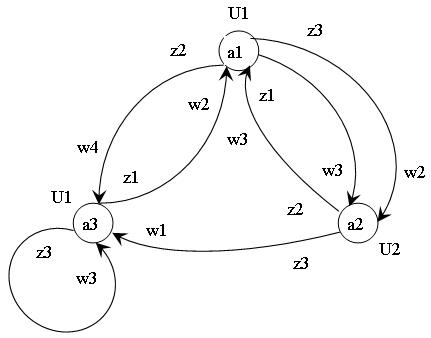
Выпишем коды состояний входных сигналов и выходных сигналов 1, 2 рода - Т-11-14.

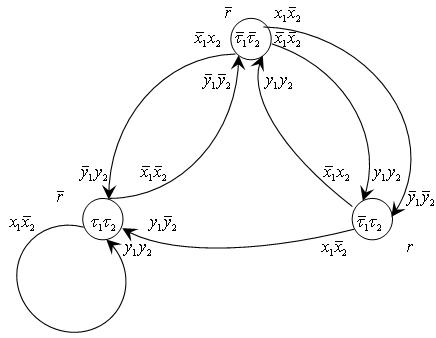
Из таблицы функции кодов для элементов задержки Т-19 видно что если в некотором состоянии элемент П_i принимает значение 1, то на всех переходах в это состояние функция возбуждения этого элемента должна принимать значение 1.

При синтезе автомата на элементах задержки все дуги графа, входящие в состояние, в котором элемент памяти принимает 1, отмечаются символом _i при i =1..I, где I - длина кода состояний.
Очевидно, что в каждой дуге графа автомата будет приписано столько символов, сколько единиц содержится в коде состояния, в которое входит эта дуга.

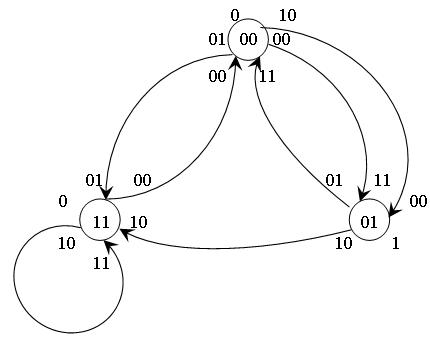
Выражение для _i получается, как дизъюнкция выражений, каждое из которых представляет собой конъюнкцию, соответствующую коду состояния, из которого выходит дуга, отмеченная _i и входного сигнала, приписываемого этой дуге. Если входных сигналов несколько, то берется из дизъюнкция.

Аналогично, выражения для выходного сигнала 1 рода y_n (n = 1..N), где n - число выходных каналов, получается как дизъюнкция выражений, каждое из которых представляет собой конъюнкцию, соответствующую коду состояния, из которого выходит дуга, отмеченная y_n и приписанного этой дуге входного сигнала, под действием которого происходит переход с выдачей соответствующего выходного сигнала y_n.

Выражение для выходного сигнала 2 рода r_d (d = 1..D), где D - число выходных каналов, получается как дизъюнкция конъюнкций, каждая из которых соответствует коду состояния, которому приписан символ r_d, т.е. в соответствующем этому состоянию выходного сигнала 2 рода компонента r_d = 1.

Т.к. выходные сигналы не зависят от элементов памяти, начинаем с них.

Находим, где y₁ = 1, y₂ = 1:

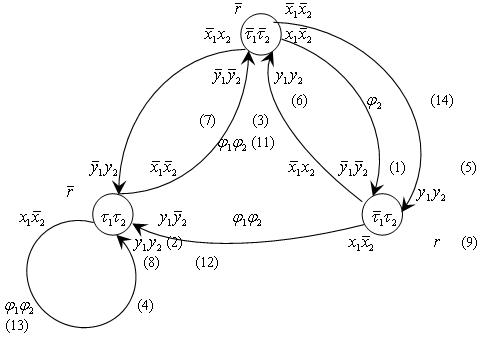
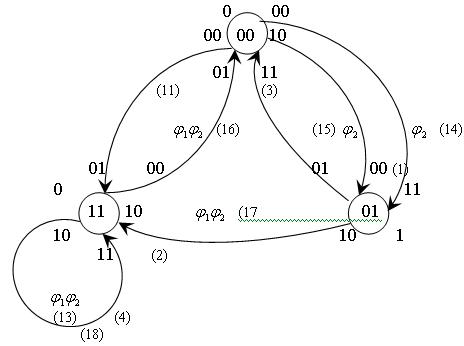
Выражение для функции возбуждения памяти на элементах задержки по графам получим таким образом:

2.4.2. Графический синтез автомата на триггерах со счетным входом

Построим автомат по таблицам Т-4-5.

Из таблицы Т-21 описывающей функцию входов триггера со счетным входом, видно, что функция возбуждения _i триггера П_i должна быть равна 1 на тех переходах, когда происходит изменение состояния этого триггера.

Теперь граф с учетом Т-11-14 будет иметь вид:


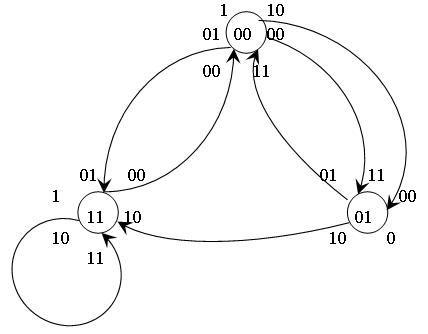
Полученных граф совпадает с графом из предыдущего пункта.

Остальная часть графа с триггерами со счетным входом строится так: если на некотором переходе из одного состояния в другое триггер П_i меняет свое состояние с 0 на 1 или с 1 на 0, то соответствующая дуга графа отмечается _i (i = 1..I). Очевидно, что каждой дуге графа будет приписано столько символов, сколько элементов памяти изменяют свои состояния на соответствующем переходе.

Формулы для y₁ и y₂ переписываем из предыдущего примера:

Теперь по графу соберем дизъюнкции конъюнкций для функции возбуждения памяти:

2.4.3. Графический синтез автомата на триггерах с раздельным входом

Функция входов триггеров с раздельными входами показывает, что для перевода триггера из 0 в 1 должен быть подан входной сигнал равный 1 на единичный вход, а для перевода из 1 в 0 - на нулевой вход. Это позволяет сформулировать процедуру синтеза С-А по графу так: каждой дуге графа приписывается набор символов из множества (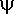 _i, _i), i = 1..I. При этом, если при переходе автомата из одного состояния в другое триггер П_i меняет свое состояние с 0 на 1, то соответствующая дуга отмечается символом _i. Если же триггер памяти переходит из 1 в 0 - дуга отмечается символом 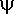_i. Каждой дуге графа так же, как и в триггерах со счетными входами будет приписано столько символов, сколько элементов памяти изменяют состояние на соответствующем переходе.

Построим граф:

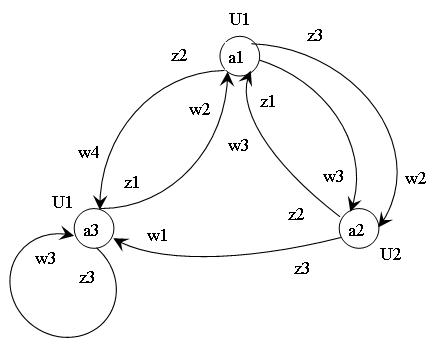
Вспомним коды состояний входных и выходных сигналов 1 и 2 типа.

Построим граф с учетом этих кодировок:

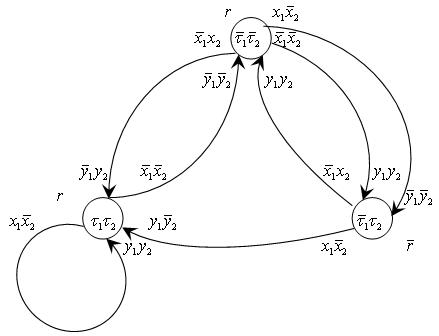
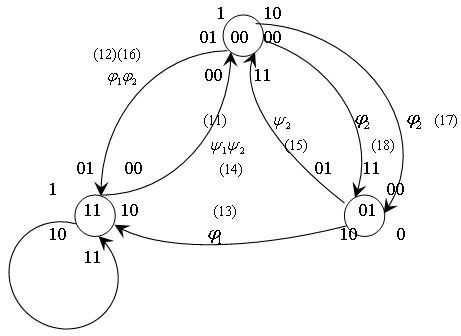
Полученный формулы совпадают с теми же формулами, полученные для других автоматов с другими триггерами, а функции возбуждения памяти синтезируется по последнему графу так:

Так же как в предыдущем примере формулы совпадают с полученным табличным синтезом.

Дата добавления: 2015-05-09