
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгоритмы функционирования цифровых автоматов
Гонки в автомате 3.2. Противогоночное кодирование 3.2.1. Суть и алгоритм развязывания состояний 3.2.2. Пример противогоночного кодирования 3.2.3. Соседнее кодирование состояний автомата 3.3. Кодирование состояний и сложность комбинационных схем 3.3.1. Кодирование состояний и КС 3.3.2. Кодирование выходных сигналов и КС 3.3.3. Оценка сложности КС 3.3.4. Пример кодирования состояний автомата
Кодирование состояний автомата
3.1. Гонки в автомате 
Задача кодирования состояний является одной из основных задач канонического метода структурного синтеза автоматов. Кодирование заключается в установлении взаимно-однозначного соответствия между множеством А = {а1,..., аМ} состояний автомата и множеством R-компонентных векторов {К1,..., КМ}, Кm = (еm1,..., emR), где еmr - состояние r-го элемента памяти, r = 1,..., R. Если еmr 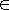 {0, 1}, т.е алфавит состояний элементов памяти двоичный, R
{0, 1}, т.е алфавит состояний элементов памяти двоичный, R  ] log2M [. Далее ради простоты ограничимся использованием в качестве элементов памяти RS-триггеров, которые будем обозначать T1,..., ТR.
] log2M [. Далее ради простоты ограничимся использованием в качестве элементов памяти RS-триггеров, которые будем обозначать T1,..., ТR.
Переход автомата из одного состояния в другое осуществляется за счет изменения состояний элементов памяти. Так, если автомат переходит из состояния аm с кодом 0101 в состояние аs с кодом 1001, то это означает, что триггер Т1 переходит из состояния 0 в состояние 1, триггер Т2 - из состояния 1 в состояние 0, а состояния триггеров Т3 и Т4 не изменяются.
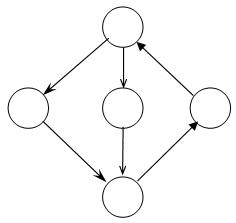
При функционировании автомата могут появиться так называемые состязания. Явление состязаний возникает вследствие того, что элементы памяти имеют различные, хотя и достаточно близкие, времена срабатывания. Кроме того, различны также задержки сигналов возбуждения, поступающих на входные каналы элементарных автоматов по логическим цепям неодинаковой длины. Если при переходе автомата из одного состояния в другое должны изменить свои состояния сразу несколько запоминающих элементов, то между ними начинаются состязания. Тот элемент, который выиграет эти состязания, т.е. изменить свое состояние ранее, чем другие элементы, может через цепь обратной связи изменить сигналы на входах некоторых запоминающих элементов до того, как другие участвующие в состязаниях элементы изменять свои состояния. Это может привести к переходу автомата в состояние, не предусмотренное его графом. Поэтому в процессе перехода из состояния аm в состояние аs под действием входного сигнала zf (рис. 1, а) автомат может оказаться в некотором промежуточном состоянии аk или аl в зависимости от того, какой элемент памяти выиграет состязания. Если затем при том же входном сигнале автомат из ak и al перейдет в состояние аs, то такие состязания являются допустимыми, или некритическими. Если же в этом автомате есть переход, например, из аk в aj 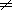 as под действием того же сигнала zf (рис. 1, б), то автомат может перейти в aj, а не в as и правильность его работы тем самым будет нарушена. Такие состязания называются критическими состязаниями или гонками. При кодировании состояний гонки должны быть устранены. Кодирование с устранением гонок называется противогоночным.
as под действием того же сигнала zf (рис. 1, б), то автомат может перейти в aj, а не в as и правильность его работы тем самым будет нарушена. Такие состязания называются критическими состязаниями или гонками. При кодировании состояний гонки должны быть устранены. Кодирование с устранением гонок называется противогоночным.

Одни из способов ликвидации гонок состоит в тактировании входных сигналов автомата импульсами определенной длительности. Предполагается, что кроме входных каналов x1,..., xL имеется еще один канал p от генератора синхроимпульсов (ГСИ), по которому поступает сигнал р = 1 в момент прихода импульса и р = 0 при его отсутствии. В связи с этим входным сигналом на переходе (am, as) будет не zf, a pzf. Тогда, если длительность импульса tp меньше самого короткого пути прохождения тактированного сигнала обратной связи по комбинационной схеме, то к моменту перехода в промежуточное состояние ak (рис. 1, б) сигнал р равен нулю и, следовательно, pzf = 0, что исключает гонки.
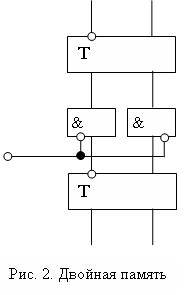
Другой способ ликвидации гонок заключается во введении двойной памяти (рис. 2). В этом случае каждый элемент памяти дублируется, причем перепись из нижнего элемента памяти в верхний происходит в момент отсутствия тактирующего импульса (р = 0). Сигналы обратной связи для получения функции возбуждения и функций выходов автомата снимаются с верхнего ряда триггеров. Таким образом, состязания могут возникнуть только между нижними триггерами, сигналы обратной связи не смогут измениться до тех пор, пока р не станет равным нулю. Но тогда входной сигнал pzf, также равен нулю, а потому гонок быть не может.
3.2. Противогоночное кодирование 
3.2.1. Суть и алгоритм развязывания состояний 
Пусть ( ,
, 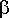 ) и (
) и ( ,
,  ) - две пары двоичных кодов длины R. Эти пары будут называться развязанными, если при некотором I (1
) - две пары двоичных кодов длины R. Эти пары будут называться развязанными, если при некотором I (1  i
i  I) i-разряд кода принимает значение 1 на паре (
I) i-разряд кода принимает значение 1 на паре ( ,
, 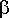 ) и противоположное значение на паре (
) и противоположное значение на паре ( ,
,  ). Если это не соблюдается, пары называются связанными.
). Если это не соблюдается, пары называются связанными.
Теорема. В автомате, состояние которого закодировано двоичными кодами конечной длины, гонки отсутствуют тогда и только тогда, когда для любых двух переходов (am, as) и (ak, al) при as 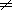 al, происходящие под действием одного и того же входного сигнала соответствующие пары развязаны.
al, происходящие под действием одного и того же входного сигнала соответствующие пары развязаны.
Алгоритм противогоночного кодирования основан на этой теореме, идея состоит в следующем: последовательно просматривая все пары переходов, имеющие хотя бы 1 общий входной сигнал, осуществляющий эти переходы, следует присваивать разрядам кодов такие значения, чтобы эти пары кодов состояний были развязаны.
Пусть (am, as) и (ak, al) пары переходов автомата, а  ,
, 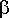 ,
,  ,
,  - соответственно четверка кодов состояний am, as, ak, al длины i.
- соответственно четверка кодов состояний am, as, ak, al длины i.
Примечание. Четверка кодов  ,
, 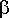 ,
,  ,
,  состоит из 0, 1 и Х.
состоит из 0, 1 и Х.
Алгоритм развязывания пар:
1. Если при некотором r (1  r
r  R) значения r-разряда четверки
R) значения r-разряда четверки  ,
, 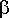 ,
,  ,
,  образуют набор 0011, пара переходов считается развязанной и переходит к следующей паре.
образуют набор 0011, пара переходов считается развязанной и переходит к следующей паре.
2. Если при некотором r (1  r
r  R) значение r-разряда четверки
R) значение r-разряда четверки  ,
, 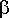 ,
,  ,
,  образует один из наборов
образует один из наборов
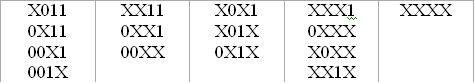
следует доопределить неопределенные значения r-разряда четверки так, чтобы его значения образовали набор 0011. Переход к следующей паре.
3. Если при некотором r (1  r
r  R) значение r-разряда четверки
R) значение r-разряда четверки  ,
,  ,
,  ,
,  образует набор 1100, пара считается развязанной. Переход к следующей паре.
образует набор 1100, пара считается развязанной. Переход к следующей паре.
4. Если при некотором r (1  r
r  R) значение r-разряда четверки
R) значение r-разряда четверки  ,
, 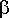 ,
,  ,
,  образует один из наборов
образует один из наборов
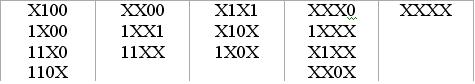
следует доопределить неопределенные значения r-разряда четверки так, чтобы его значения образовали набор 1100. Переход к следующей паре.
В результате развязывания пар переходов длина кода оказывается не минимальной, т.к. при введении нового разряда могут быть развязаны пары, которые были развязаны раньше. Следовательно алгоритм противогоночного кодирования предусматривает минимизацию длины получаемых кодов состояний. Суть заключается в следующем: исключается 1 из разрядов кодов, в результате чего некоторые пары могут оказаться связанными. Применяют алгоритм развязывания. Исключают еще 1 разряд. Снова применяют алгоритм развязывания. И так до тех пор пока длина кода не перестанет уменьшаться. Если в результате работы алгоритма некоторые значения разрядов буду неопределенны, то их определяют произвольно.
3.2.2. Пример противогоночного кодирования 
1. Развязывание пар переходов
Рассмотрим алгоритм противогоночного кодирования на примере автомата, функция переходов которого задана таблицей (Т. 3-1).
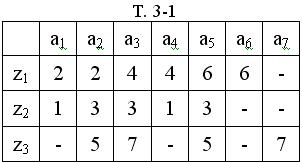
Пары переходов происходящих под действием сигналов z1, z2, z3 образуют массивы М1, М2, М3.
М1 = ((а1, а2), (а2, а2), (а3, а4), (а4, а4), (а5, а6), (а6, а6)).
М2 = ((а1, а1), (а2, а3), (а3, а3), (а4, а1), (а5, а3)).
М3 = ((а2, а5), (а3, а7), (а5, а5), (а7, а7)).
Начинаем развязывать пары из М1. Переход (а1, а2) с (а2, а2) развязывать не надо, т.к. состояние а2 и а2 совпадают. Пару переходов (а1, а2) и (а3, а4) будем развязывать введение переменной  1, такой как в (Т. 3-2).
1, такой как в (Т. 3-2).

Пара (а1, а2) и (а4, а4) оказываются развязанными, так как этой паре соответствует четверка 0011. Пара (а1, а2) и (а5, а6) образуют четверку 00ХХ, которую развязываем до 0011 по 2 пункту алгоритма - получаем таблицу Т. 3-3.

Теперь развязанными оказываются пары (а1, а2) и (а6, а6), (а2, а2) и (а3, а4), (а2, а2) и (а4, а4), (а2, а2) и (а5, а6), (а2, а2) и (а6, а6). Обратимся к паре (а3, а4) (а5, а6) - эта пара имеет четверку 1111. Пара неразвязанная. Введем дополнительную переменную 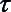 2.
2.
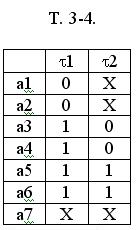
Остальные переходы в массиве М1 оказываются развязанными.
Аналогично для М2 и М3 получим таблицы.
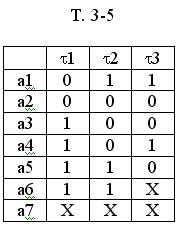

2. Минимизация кодов состояний
В таблице Т. 3-6 исключаем первый столбик и получаем таблицу Т. 3-7.
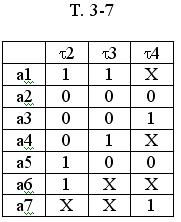
Начинаем повторно процесс развязывания. Оказывается, что по 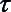 2 не развязана пара (а1, а2) (а5, а6). Добавляем еще одну переменную
2 не развязана пара (а1, а2) (а5, а6). Добавляем еще одну переменную  5.
5.
Все остальные пары по 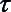 2 являются развязанными. Далее исключаем
2 являются развязанными. Далее исключаем 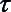 2.
2.
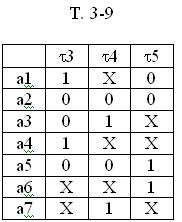
В Т. 3-9 развязывание пар не требуется, так как после проверки устанавливается, что все пары оказываются развязаны. Дальнейшая минимизация невозможна, так как ]ld7[ = 3 (3 переменных, 7 состояний). После доопределения Х в таблице Т. 3-9 получаем таблицу Т. 3-10 противогоночного кодирования.
3.2.3. Соседнее кодирование состояний автомата 
Существует 1 частный способ кодирования - соседнее кодирование. Условие отсутствия гонок при соседнем кодировании всегда выполняется. Суть этого кодирования состоит в том, что 2 состояния связанные дугой графа кодируются наборами, отличающимися лишь в 1 элементе памяти. Существует несколько алгоритмов, но они не всегда поддаются формализации.
Соседнее кодирование однако не всегда возможно. Требование к графу автомата, допускающего соседнее кодирование таково:
1) В графе не должно быть циклов с нечетными числом вершин.
2) 2 соседних состояния не должны иметь более двух состояний, лежащих между ними.
3.3. Кодирование состояний и сложность комбинационных схем 
3.3.1. Кодирование состояний и КС 
Вспомним синтез автомата на линиях задержки, таблица переходов которого Т. 4.

В таблице Т. 15 состояние автомата кодируется так: к(а1) = 00, к(а2) = 01, к(а3) = 11.
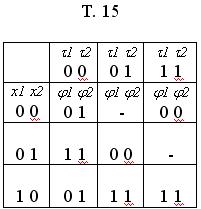
В результате синтеза, функция возбуждения имеет такой вид:

Будем кодировать состояния автомата так: к(а1) = 01, к(а2) = 10, к(а3) = 00. Таблица переходов Т. 3-11 будет такой:

Так как таблица функции возбуждения при синтезе на линиях задержки совпадает с таблицей переходов, непосредственно с таблицей Т. 3-11, имеют такие функции возбуждения.

Рассмотрим алгоритм, который используется при кодировании состояний и позволяет упростить функции возбуждения:
1) каждому состоянию  ставим в соответствие число Nm равное числу переходов в это состояние, или равное числу ветвей, входящих в это состояние на графе;
ставим в соответствие число Nm равное числу переходов в это состояние, или равное числу ветвей, входящих в это состояние на графе;
2) числа N1, N2,…,NM сортируются по убыванию;
3) состояние аt c наибольшим Nt кодируется кодом 0000…0;
4) следующие I-состояний (I - число элементов памяти) кодируется кодами с одной "1": (00..01), (00..10),…,(10...00);
5) следующие I-состояний из оставшихся кодируются кодами содержащие две "1".
В результате получаем такое кодирование, при котором чем больше переходов в некоторое состояние, тем меньше единиц содержит код этого состояния.
3.3.2. Кодирование выходных сигналов и КС 
Аналогичные соображения могут быть использованы и при кодировании выходных сигналов для минимизации функции выходов. Вспомним таблицу выходов абстрактного С-автомата Т.5.
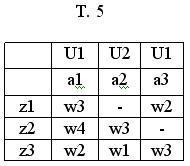
Упорядочим выходные сигналы автомата по частоте их появления в таблице графа.
w3 - 3 раза
w2 - 2 раза
w1 - 1 раз
w4 - 1 раз
U1 - 2 раза
U2 - 1 раз
Закодируем выходной сигнал первого и второго рода Т. 3-12, Т. 3-13.
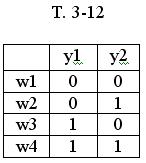
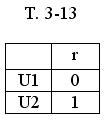
Таблица выходов теперь будет такой:
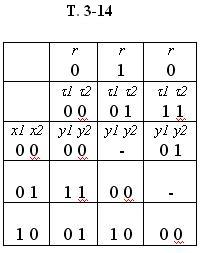
Непосредственно из таблицы Т. 3-14 получаем выражение для функции выходов:

3.3.3. Оценка сложности КС 
Введем весовую функцию
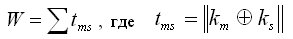
- расстояние между кодами состояний аm и as, равное числу элементов, которые изменяют свое значение при переходе из состояния аm в as.
Функция W, сумма произведений по всем возможным переходам, и служит оценкой сложности КС. Чем меньше значение функции, тем проще КС.
Рассмотрим один из самых распространенных алгоритмов:
1) строится матрица-столбец
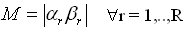
состоящая из всех различных пар номеров, так что в автомате есть переход из  r в
r в 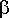 r;
r;
2) упорядочить строки в матрице так, чтобы выполнялось условие
 .
.
Это означает, что хотя бы один из элементов r-строки содержится в какой-нибудь из предыдущих строк. Для связных графов это всегда возможно;
3) закодируем состояние из 1 строки матрицы М таким образом, что
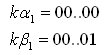
4) вычеркиваем из М одну строку, соответствующую закодированным состояниям  a1,
a1,  b1
b1
5) в силу условия пункта 2 в 1 строке новой матрицы М1 оказывается закодированным 1 элемент. Другой незакодированный элемент обозначим через  ;
;
6) выбрав из матрицы М1 все строки, содержащие  , построим матрицу М
, построим матрицу М  . В этой матрице выберем множество элементов В
. В этой матрице выберем множество элементов В  = (
= ( f),
f),  f = 1,.., F, которые уже закодированы. Их обозначим k
f = 1,.., F, которые уже закодированы. Их обозначим k  1, k
1, k  2, …, k
2, …, k  f;
f;
7) для каждого k  f (f = 1, …, F) находится множество кодов соседних с k
f (f = 1, …, F) находится множество кодов соседних с k  f и еще не занятых для кодирования состояния автомата. Это множество
f и еще не занятых для кодирования состояния автомата. Это множество
 .
.
Может оказаться, что
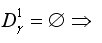
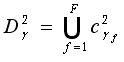
где c  f это множество кодов, у которых кодовое расстояние с кодом k
f это множество кодов, у которых кодовое расстояние с кодом k  f равно 2. Если и это
f равно 2. Если и это
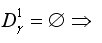
делаем дальше
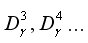
пока не найдется
 .
.
Обозначим
 .
.
8) для каждого кода k  g находим кодовое расстояние между этим кодом и всеми используемыми кодами k
g находим кодовое расстояние между этим кодом и всеми используемыми кодами k  f
f
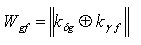 .
.
9) находим
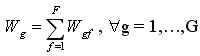
Если в автомате имеются переходы из 1 состояния в другое и обратно, вес перехода входит в Wg дважды.
10) из множества Dn  выбираем код k
выбираем код k  , у которого вес Wg = min Wg. Состояние a
, у которого вес Wg = min Wg. Состояние a  кодируется кодом k
кодируется кодом k  .
.
11) из матрицы М1 вычеркиваем строки, где закодированы оба элемента. Получаем М2. Если в ней не осталось ни одной строчки, то переходим к пункту 12, иначе - к 5.
12) вычисляем функцию
 .
.
Оценкой качества кодирования служит число
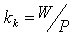 ,
,
где Р - число переходов. Значение kк лежит в пределах [1 - I], чем ближе к 1, тем лучше автомат.
3.3.4. Пример кодирования состояний автомата 
Рассмотрим автомат представленный графом
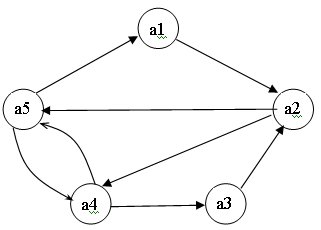
Дугам графа входные и выходные сигналы не приписываются, т.к. они в работе алгоритма кодирования состояния не участвуют.
Строим матрицу М.

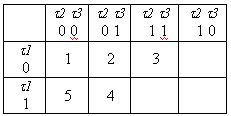
Кодируем первую строчку: k1 = 000, k2 = 001. Расположим эти коды в карте Карно.
Из матрицы вычеркиваем первую строчку и получаем матрицу М1.
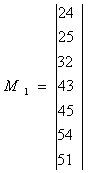
В первой строке М1 не закодирован элемент  = 4. Собираем матрицу из этих элементов.
= 4. Собираем матрицу из этих элементов.
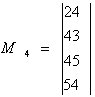
В М4 уже закодирован элемент "2", ==> множество В4 = (2). Для элемента "2" с кодом 001 строим множество С12, которое получаем инвертируя элементы этого множества.
С12 = (101, 011).
С12 объединяем (если их несколько) и получаем объединение D14 = (101, 011). Находим весовые функции элементов с исходными кодами
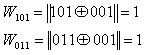
Для элемента а4 можно взять любой из этих кодов, так как оба они равны единице. Возьмем код k4 = 101. Заносим его в карту Карно
В М1 удаляем 1 строку и получаем М2
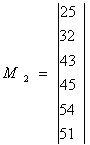
В первой строке М2 не закодированным оказывается элемент  = 5. Собираем матрицу М5
= 5. Собираем матрицу М5
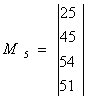
Множество В5 = (2, 4, 1). Коды этих элементов: "2" - 001, "4" - 101, "1" - 000.
Неиспользуемые смежные коды будут:
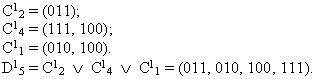
Находим весовые функции:
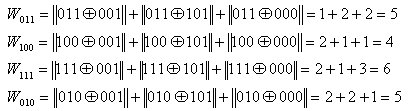
Надо взять число, которое дает минимальное расстояние: W100 = min (W011, W100, W111, W010).
Этим кодом и будет закодирован элемент а5 - k5 = 100.
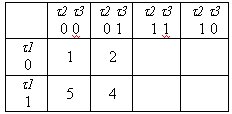
В М2 удаляем 1 строчку и все строки, в которых элементы уже закодированы
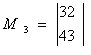
 = 3 - незакодирован. Матрица, состоящая из строчек с незакодированными элементами совпадает с матрицей М3.
= 3 - незакодирован. Матрица, состоящая из строчек с незакодированными элементами совпадает с матрицей М3.
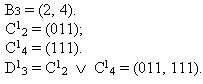
Весовые функции:
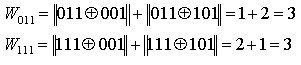
k3 = 100
Все состояния оказываются закодированными.
Весовая функция всего автомата:
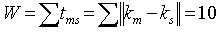
Число переходов самого автомата равно 8 (Р = 8).
Коэффициент качества кодирования:
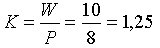
4.1. Микропрограммы работы дискретных устройств
4.2. Граф-схемы алгоритмов (ГСА)
4.2.1. Определение ГСА
4.2.2. Пример ГСА
4.2.3. Процесс выполнения ГСА
4.2.4. Пример работы дискретного устройства по ГСА
4.1. Микропрограммы работы дискретных устройств 
При описании широкого класса дискретных систем в автомате, вычислительной технике и телефонии оказывается удобным представлять эти системы в виде двух частей:
1) операционные устройства (ОУ)
2) устройства управления (УУ)
В вычислительной машине к операционному устройству относят блоки памяти, регистры, сумматоры, каналы передачи информации, шифраторы и дешифраторы. К устройству управления относят ту часть машины, которая координирует действия всех перечисленных устройств, определяет последовательность преобразований при переработке информации, т.е. алгоритмическая функция этого цифрового автомата. Задачей устройства управления является выработка распределенных по времени последовательность управляющих сигналов, под действием которых в операционных устройствах осуществляется некоторая операция.
Иногда целесообразно многоступенчатое или иерархическое представление дискретного устройства или цифрового автомата, пример при проектировании цифрового управляющего устройства (ЦУУ) ЭВМ, арифметическое устройство рассматривается в целом, как часть операционного. При проектировании самого арифметического устройства, в нем выделяется свой автомат управления, а к операционной части арифметического устройства относят его регистры, сумматор, регистр кодов арифметических операций и счетчик сдвигов.
Задача синтеза операционных устройств в следствии их регулярной и большой повторяемости хорошо изучена и не представляет серьёзных трудностей. Иначе обстоит дело с устройством управления, которое является наименее регулируемой частью цифрового автомата и совершенно не повторяется при переходе от одного цифрового устройства к другому. В связи с этим проектирование устройства управления представляет наибольшую сложность и, часто проектирование цифрового автомата после выбора основных частей операционной системы, сводится к проектированию устройства управления.
Порядок выполнения операций в цифровом автомате определяется микропрограммой которая представляет собой совокупность микроопераций и логических условий. Под микрооперацией понимается элементарный единичный процесс переработки информации в дискретной системе или какой-то её части, это происходит за время одного такта работы автомата.
Для выполнения той или иной микрооперации, устройство управления должно выработать управляющие сигналы, которые называются сигналы микроопераций и обозначаются: yn,  n = {1,N}. Если в устройстве одновременно реализуется несколько микроопераций, то это множество микроопераций, будем называть микропрограммой: yt = (ytu),
n = {1,N}. Если в устройстве одновременно реализуется несколько микроопераций, то это множество микроопераций, будем называть микропрограммой: yt = (ytu),  u = {1,U}. Если yt = (yt1, …,ytu,…, ytU) - микрокоманда, то операции yt1, …,ytu,…, ytU - выполняются одновременно в один и тот же момент автоматного времени.
u = {1,U}. Если yt = (yt1, …,ytu,…, ytU) - микрокоманда, то операции yt1, …,ytu,…, ytU - выполняются одновременно в один и тот же момент автоматного времени.
Если U = 1, то микрокоманда yt - состоит из одной микрооперации. Возможен случай когда U = 0, тогда множество микроопераций, образующих микрокоманду = пусто. y0 - реализация такой микрокоманды, эквивалентной отсутствию выполнения какой-либо элементарной операции. В случае синхронных цифровых устройств, микрокоманда y0 представляется, пропускания такта, когда не поступают никакие сигналы от устройства управления к операционному устройству.
Выполнение микропрограмм состоит в последовательном выполнении отдельных микрокоманд, эта последовательность определяется логическими или булевыми функциями  ij. Множество двоичных переменных x = (xl),
ij. Множество двоичных переменных x = (xl),  l={1,L} поступает на вход устройства управления, если в микропрограмме все микрокоманды различны, то каждой паре команд yi, yj (i = j или i<>j) соответствует функция
l={1,L} поступает на вход устройства управления, если в микропрограмме все микрокоманды различны, то каждой паре команд yi, yj (i = j или i<>j) соответствует функция  ij. Если
ij. Если  ij = 1, то разрешается выполнение микрокоманды yj после микрокоманды yi.
ij = 1, то разрешается выполнение микрокоманды yj после микрокоманды yi.
Если в микропрограмме есть одинаковые микрокоманды, то их либо сводят в одну, либо перенумеровывают, так чтобы они имели разные номера. Очевидно, что среди множества функций  ir,
ir,  r = {1,R} в каждый момент времени не может быть более одной равной единице. R - число различных микрокоманд в микропрограмме. Если окажется, что число единиц больше одной, то реализация микропрограммы не может быть детерминированной, т.к. нельзя предсказать определенно, какая из микрокоманд будет выполнятся в следующий момент времени после микрокоманды yi.
r = {1,R} в каждый момент времени не может быть более одной равной единице. R - число различных микрокоманд в микропрограмме. Если окажется, что число единиц больше одной, то реализация микропрограммы не может быть детерминированной, т.к. нельзя предсказать определенно, какая из микрокоманд будет выполнятся в следующий момент времени после микрокоманды yi.
Для записи микропрограмм, работающих дискретных устройств, для записи алгоритма функции цифрового автомата используется язык граф-схем алгоритмов (ГСА), логарифмических схем алгоритмов (ЛСА) и матричных схем алгоритмов (МСА).
4.2. Граф-схемы алгоритмов 
4.2.1. Определение ГСА 
ГСА - это ориентированный связный граф, содержащий вершины четырех типов:

Начальная вершина входов не имеет, начальная и операторная вершина имеют по одному выходу, условная вершина имеет два выхода (1,0), конечная вершина выходов не имеет.
Граф должен удовлетворять следующим условиям:
1) Содержит конечное число вершин, каждая из которых принадлежит одному из перечисленных выше типов;
2) Имеет одну начальную и одну конечную вершину;
3) Входы и выходы вершин, соединяются друг с другом с помощью дуг, направленных от выхода ко входу;
4) Каждый выход соединен, только с одним входом;
5) Любой вход соединяется с одним выходом;
6) Для любой вершины графа существует, по крайне мере, один путь из этой вершины в конечную вершину;
7) Один из выходов условной вершины может соединятся с её входом, что недопустимо для операторной вершины;
8) Каждой условной вершине записывается один из элементов множества;
x = (xl)  l = {1,L}, называют его множеством логических условий, разрешается в различных, условных вершинах, записаны одинаковые элементы множества х;
l = {1,L}, называют его множеством логических условий, разрешается в различных, условных вершинах, записаны одинаковые элементы множества х;
9) В каждой операторной вершине записывается оператор или микрокоманда yt подмножество множества y = (yn)  n = {1,N}, называют его подмножеством микроопераций. yt = (yt1,…,ytu,…,ytU),
n = {1,N}, называют его подмножеством микроопераций. yt = (yt1,…,ytu,…,ytU),  u = {1,U};
u = {1,U};
При U = 0 yt = 0;
Разрешается запись в различных операторных вершинах одинаковых подмножеств множества микроопераций.
4.2.2. Пример ГСА 
Предположим, что в операторных вершинах ГСА, записаны операторы yi,...,yT, все разные так что оператор вершины, можно отождествить с записанном в ней оператором. Начальной вершине поставим оператор y0, конечной yT+1. Пусть имеется путь yi,  i = {0,T}, до вершины yj,
i = {0,T}, до вершины yj,  j = {1,T+1}. Путь имеет вид: yipi1...pir...piRyj путь этот проходит только через условные вершины pir...piR.
j = {1,T+1}. Путь имеет вид: yipi1...pir...piRyj путь этот проходит только через условные вершины pir...piR.
Очевидно что каждому пути соответствует конъюнкция  ij = xijei1
ij = xijei1 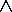 ...
... 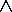 xireir
xireir 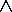 ...
... 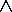 xiReiR
xiReiR
xir принадлежит Х - логическое условие, записанное в условной вершине pir
eir принадлежит {0,1} - символ, приписанный к выходу условной вершины pir, через которую проходит указанный путь.
xir1 = xir
xir0 = xir
В общем виде:  ij =
ij = 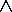 xireir
xireir
Схема:

Если между вершинами yi и yj имеются несколько путей, проходящих через условные вершины, то  ij, получится как дизъюнкция этих конъюнкций, т.е.
ij, получится как дизъюнкция этих конъюнкций, т.е.  ij =
ij = 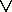
 ijh; H - число путей, соединяющих вершину yi и yj, а
ijh; H - число путей, соединяющих вершину yi и yj, а  ijh - конъюнкция соответствующая h - пути из yi в yj
ijh - конъюнкция соответствующая h - пути из yi в yj  ij - называется функцией перехода от оператора или микрокоманды yi к оператору yj. Очевидно что множество функций
ij - называется функцией перехода от оператора или микрокоманды yi к оператору yj. Очевидно что множество функций  ij,…,
ij,…,  шT+1 - является ортогональным, т.е.
шT+1 - является ортогональным, т.е.  ij
ij 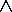
 ik = 0,
ik = 0,  j, k = {1, T+1} и полным, значит
j, k = {1, T+1} и полным, значит 
 ij = 1;
ij = 1;
4.2.3. Процесс выполнения ГСА 
Всевозможные наборы значений переменных х1,…,xL обозначим через  1,…,
1,…,  2L.
2L.
Определим процесс выполнения ГСА, начиная с оператора y0 на произвольной бесконечной последовательности наборов  mi,...,
mi,...,  mq следующим образом: Выписываем начальный оператор y0.
mq следующим образом: Выписываем начальный оператор y0.
1) Придаем переменным x1,...,xL значения из набора  m1, из множества функций перехода
m1, из множества функций перехода  01,...,
01,...,  0T выбираю функцию
0T выбираю функцию  0i1, i1 принадлежит {1, T} принимает значение 1 на этом наборе.
0i1, i1 принадлежит {1, T} принимает значение 1 на этом наборе.  0i1(
0i1( mi) = 1. В строчку рядом с y0 приписываем yi1.
mi) = 1. В строчку рядом с y0 приписываем yi1.
2)Придаем переменным x1,...,xL значения из набора  m2 из множества функций
m2 из множества функций  i11,...,
i11,...,  i1T, выбираем функцию
i1T, выбираем функцию  i1i2, i2 принадлежит {1,T}, так что
i1i2, i2 принадлежит {1,T}, так что  i1i2 (
i1i2 ( m2) = 1. В строчку рядом приписываем yi2 и т.д.
m2) = 1. В строчку рядом приписываем yi2 и т.д.
Пусть перед некоторым q-ым шагом имеем строчку операторов y0yi1yi2...yiq-1 если на наборе  mq некоторая функция
mq некоторая функция  iq-1iq = 1, то то в выписанную строчку добавляем оператор yiq. Если оказывается, что
iq-1iq = 1, то то в выписанную строчку добавляем оператор yiq. Если оказывается, что  iq-1T+1 (
iq-1T+1 ( mq) = 1, то в строку вслед за yiq-1, приписываем оператор yT+1 и процесс выполнения алгоритма ГСА прекращается. Если строчка y0yi1yi2yig-1,...,yig эта строчка называется значения ГСА на последовательном наборе
mq) = 1, то в строку вслед за yiq-1, приписываем оператор yT+1 и процесс выполнения алгоритма ГСА прекращается. Если строчка y0yi1yi2yig-1,...,yig эта строчка называется значения ГСА на последовательном наборе  m1,..,
m1,..,  mq; если каждому оператору yt
mq; если каждому оператору yt  t = {0, T+1}, поставлено в соответствие некоторое множество Bt логических условий, элементы которого могут изменяться во времени выполнения оператора yt то говорят, что задано распределение сдвигов. Это является дополнительной информацией о логике работы устройства и эта дополнительная информация может быть использована для минимизации ГСА.
t = {0, T+1}, поставлено в соответствие некоторое множество Bt логических условий, элементы которого могут изменяться во времени выполнения оператора yt то говорят, что задано распределение сдвигов. Это является дополнительной информацией о логике работы устройства и эта дополнительная информация может быть использована для минимизации ГСА.
Пусть процесс выполнения ГСА рассмотрим для некоторой последовательности наборов  m1
m1  m2,...,
m2,...,  mq
mq  mq+1 И пусть набор предшествует моменту выполнения оператора yiq, а
mq+1 И пусть набор предшествует моменту выполнения оператора yiq, а  mq+1 в момент выполнения оператора yiq.
mq+1 в момент выполнения оператора yiq.
Последовательность наборов называется допустимой для ГСА если при заданном распределении сдвигов всякий набор  mq+1 либо совпадает с набором
mq+1 либо совпадает с набором  mq, либо отличается от него только значением переменной Biq.
mq, либо отличается от него только значением переменной Biq.
Если ГСА Г1 И Г2 равносильны при данном распределении сдвигов Г1 =Г2, то для всякой последовательности наборов, допустимых для ГСА Г1 и Г2, значения этих ГСА при данных распределениях сигналов совпадают.
4.2.4. Пример работы дискретного устройства по ГСА 
Функционирование дискретного устройства на примере. Приведенный ГСА имеет 1 начальную, 1 конечную, 16 условных и 1 операторную вершину, т.к. для этой граф-схемы X =(x1,…,x8) Y =(y1,...,y11), то у соответствующего устройства должно быть 8 входных и 11 выходных каналов, т.е. предположим, что для каждой микрооперации имеется выходной канал. В общем случае, если число микрооператоров n, т.е. Y = (y1,y2,... yn,...,yN), то каждому оператору Yt=(yt1,...,ytu,...,ytU) соответствует векторный выходной сигнал y1,..,yn,...,yN компоненты которого определяются так:
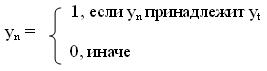
|
|
Дата добавления: 2015-05-09; Просмотров: 6015; Нарушение авторских прав?; Мы поможем в написании вашей работы!