Работа, совершаемая телом при изменениях его объема

Взаимодействие данного тела с соприкасающимися с ним телами можно охарактеризовать давлением, которое оно на них оказывает. С помощью давления можно описать взаимодействие газа со стенками сосуда, а также твердого или жидкого тела со средой (например, газом), которая его окружает. Перемещение точек приложения сил взаимодействия сопровождается изменением объема тела. Следовательно, работа, совершаемая данным телом над внешними телами, может быть выражена через давление и изменение объема тела. Чтобы найти это выражение, рассмотрим следующий пример.

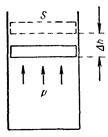
Пусть газ заключен в цилиндрический сосуд, закрытый плотно пригнанным легко скользящим поршнем (рис.). Если по каким-либо причинам газ станет расширяться, он будет перемещать поршень и совершать над ним работу. Элементарная работа, совершаемая газом при перемещении поршня на отрезок Dh, равна D’A = f Dh, где f – сила, с которой газ действует на поршень. Заменяя эту силу произведением давления газа р на площадь поршня S, получаем: D’A = pS Dh. Но S Dh представляет собой приращение объема газа DV. Поэтому выражение для элементарной работы можно записать следующим образом:

D'A = pDV. (96.1)

Если давление газа остается постоянным (для этого должна одновременно изменяться соответствующим образом температура), работа, совершаемая при изменении объема от значения V₁ до значения V₂, равна

А₁₂ = р(V₂- V₁). (96.2)

Если же при изменении объема давление не остается постоянным, формула (96.1) справедлива только для достаточно малых DV. В этом случае работа, совершаемая при конечных изменениях объема, должна вычисляться как сумма элементарных работ вида (96.1), т. е. путем интегрирования:

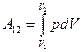(96.3)

Найденные выражения для работы справедливы при любых изменениях объема твердых, жидких и газообразных тел.

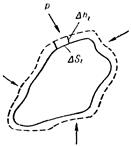
На рисунке изображено твердое тело произвольной формы, погруженное в жидкую или газообразную среду, которая оказывает на тело одинаковое во всех точках давление р. Пусть тело расширяется так, что отдельные элементарные участки его поверхности DS_i получают различные перемещения Dh_i. Тогда i-й участок совершит работу D'А_i, равную pDS_iDh_i. Работа, совершаемая телом, может быть найдена как сумма работ отдельных участков: D'A = SD'A_i = S p DS_i Dh_i. Вынося за знак суммы одинаковое для всех участков р и замечая, что S D S _i D h i дает приращение объема тела DV, можно написать: D’A=pDV, т. е. и в общем случае оказывается справедливой формула (96.1).

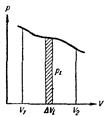
Иллюстрацией соотношения (96.3) является рисунок слева, представляющий процесс изменения объема тела на диаграмме (р, V). Элементарной работе D'A_i = р_iDV_i, соответствует площадь узкой заштрихованной полоски на графике. Очевидно, что площадь, ограниченная осью V, кривой p = f(V) и прямыми V₁, и V₂, численно равна работе, совершаемой при изменении объема от значения V₁ до V₂. При использовании выражения (96.1) (с переходом к дифференциалам), уравнение (95.4) первого начала термодинамики можно написать следующим образом:
d'Q = dU + pdV.

Температура. Измерение температуры.

К определению понятия температуры можно прийти на основании следующих соображений. Если несколько соприкасающихся тел находятся в состоянии теплового равновесия, т. е. теплопередача отсутствует, то этим телам приписывается одинаковая температура. Если при установлении теплового контакта между телами одно из них передает энергию другому посредством теплопередачи, то первому телу приписывается большая температура, чем второму. От температуры зависит ряд свойств тел – объем, электрическое сопротивление и т. п. Любое из этих свойств может быть использовано для количественного определения температуры.

Если тело, выбранное для измерения температуры (термометрическое тело), в находится в тепловом равновесии с тающим льдом, телу можно в этом случае приписать температуру 0° и, тем самым, охарактеризовать количественно то свойство тела (температурный признак), которое можно использовать для измерения температуры. Пусть в качестве такого признака выбран объем тела и значение его при 0° равно V₀. Затем то же тело можно привести в тепловое равновесие с кипящей под атмосферным давлением водой. В этом состоянии ему можно сопоставить значение температуры, равное 100°, и определить соответствующий объем V₁₀₀. Принимая, что выбранный нами температурный признак (объем) изменяется с температурой линейно, состоянию, в котором термометрическое тело имеет объем V, следует приписать температуру

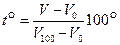(97.1)

Установленная таким образом температурная шкала называется, как известно, шкалой Цельсия. Соотношение, аналогичное (97.1), можно написать и для случая, когда для измерения температуры берется не объем, а какой - либо иной температурный признак.

Проградуировав описанным способом термометр, его можно использовать для измерения температуры, приводя в тепловое равновесие с тем телом, температура которого нас интересует, и, производя отсчет величины объема.

При сравнении термометров, использующих различные по природе термометрические тела (например, ртуть и спирт) или различные температурные признаки (например, объем и электрическое сопротивление), обнаруживается, что показания этих термометров, совпадая из-за способа градуировки при 0° и 100°, не совпадают при других температурах. Отсюда следует, что для однозначного определения температурной шкалы необходимо условиться, кроме способа градуировки, также о выборе термометрического тела и температурного признака.

Забегая вперед, укажем, что может быть установлена температурная шкала, не зависящая от свойств термометрического тела. Эта шкала называется абсолютной шкалой температур.

Уравнение состояния идеального газа. Абсолютная температура.

Состояние некоторой массы газа определяется значениями трех параметров: давления р, объема V и температуры t°. Эти параметры закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение других. Указанная связь может быть задана аналитически в виде некоторой функции

F(p, V, t^o) = 0. (98.1)

Соотношение, дающее связь между параметрами какого-либо тела, называется уравнением состояния этого тела. Следовательно, (98.1) представляет собой уравнение состояния данной массы газа. Если разрешить (98.1) относительно какого-либо из параметров, например р, уравнение состояния примет вид

p = f(V, t^o) (98.2)

Известные из школьного курса законы Бойля – Мариотта и Гей-Люссака дают уравнения состояния для случаев, когда один из параметров остается постоянным. Так, например, закон Бойля – Мариотта гласит, что для данной массы газа при постоянной температуре давление газа изменяется обратно пропорционально его объему. Аналитически это можно записать следующим образом:

pV = const (t ° = const). (98.3)

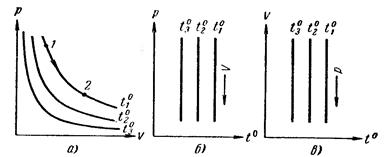
Совокупность состояний, отвечающих одной и той же температуре, изобразится на диаграмме (р, V) кривой, определяемой уравнением (98.3), т. е. гиперболой. Каждому значению температуры соответствует своя кривая (рис. 216,о). Эти кривые называются изотермами («изо» – одинаковый, равный). Переход газа из одного состояния в другое, совершающийся при постоянной температуре, называется изотермическим процессом.

При изотермическом процессе точка, изображающая состояние газа, перемещается по изотерме. На диаграмме (р, t °) или (V, t °) изотермический процесс изображается прямой, параллельной оси р (соответственно V). Эти прямые также будут изотермами. Третий параметр V (соответственно р) не сохраняет вдоль этих прямых постоянного значения, возрастая при перемещении по прямой в указанном стрелкой направлении (рис. 216,6 и в). Закон Гей-Люссака гласит, что при неизменном давлении объем данной массы газа меняется линейно с температурой:

V= V₀(l+ at°) (p = const). (98.4)

Аналогичная зависимость имеется для давления при постоянном объеме:

p= p₀(l+at°) (V = const). (98.5)

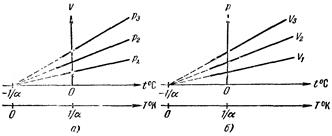
В этих уравнениях t° – температура по шкале Цельсия, V₀ – объем при 0°С, p₀ – давление при 0°С. Коэффициент a в обоих уравнениях одинаков и имеет значение 1/273 град^-1. Процесс, протекающий при постоянном давлении, называется изобарическим. Для газа такой процесс изобразится на диаграмме (V, t°) прямой (98.4) (рис. a; различные прямые отвечают разным давлениям).

Эта прямая называется изобарой. Отметим, что на диаграмме (р, t°) или (р, V) изобара имеет вид прямой, параллельной оси t° или соответственно оси V. Процесс, протекающий при постоянном объеме, называется изохорическим. На диаграмме (p,t°) изохоры имеют вид, показанный на рис. б. Заметим, что, как следует из (98.4) и (98.5), все изобары и все изохоры пересекают ось t° в одной и той же точке, определяемой из условия 1 + at° = О, откуда t°= -1/a = -273,15° С

Смещение начала отсчета температур в эту точку есть переход от шкалы температур Цельсия к другой температурной шкале, которая называется абсолютной (или шкалой Кельвина). В соответствии с определением абсолютной шкалы, между абсолютной температурой Т и температурой по Цельсию t° имеется следующее соотношение:

T = t° + 1/a = t° + 273,15. (98.6)

Так, например, температуре 0°С соответствует 273,15° К. Температура, равная 0°К, называется абсолютным нулем, ему соответствует –273,15 °С.

Переход от температуры по Цельсию к абсолютной температуре (t° = Т– 1/a) преобразует уравнения (98.4) и (98.5) к виду

V = V₀(1 + at°) = V0[1 + a(T–1/a)] = aV₀T (98.7)

и аналогично:

p = ap₀T (98.8)

Из этих уравнений следует, что

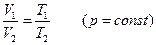(98.9)

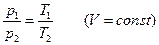, (98.10)

где индексы 1 и 2 относятся к произвольным состояниям, лежащим на одной и той же изобаре [в случае (98.9)] или на одной и той же изохоре [в случае (98.10)].

Законы Бойля – Мариотта и Гей-Люссака являются приближенными. Всякий реальный газ тем точнее следует уравнениям (98.3), (98.9) и (98.10), чем меньше его плотность, т. е. чем больший объем он занимает. В соответствии с (98.3) объем растет с уменьшением давления, а согласно (98.9) объем возрастает с температурой. Следовательно, законы Бойля – Мариотта и ГейЛюссака справедливы при не слишком низких температурах и невысоких давлениях. Газ, который точно следует уравнениям (98.3), (98.9) и (98.10), называется идеальным. Идеальный газ представляет собой абстракцию. Всякий реальный газ по мере убывания его плотности все больше приближается по свойствам к идеальному. Некоторые газы, такие, как воздух, азот, кислород, при комнатной температуре и атмосферном давлении весьма близки к идеальному газу. Особенно близки по своим свойствам к идеальному газу гелий и водород.

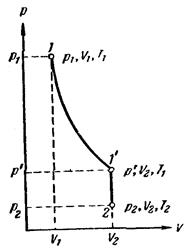
Объединив уравнения Бойля – Мариотта и Гей – Люссака, можно найти уравнение состояния идеального газа. Для этого возьмем на диаграмме (р, V) два произвольных состояния, определяемых значениями параметров p₁, V₁, Т₁, и р₂, V₂, T₂ (рис.). Рассмотрим процесс перехода из 1 в 2, состоящий из изотермы 1 – 1' и изохоры 1' – 2. Температура состояния 1', очевидно, совпадает с температурой состояния 1, а объем в 1' равен объему в состоянии 2. Давление р', вообще говоря, отлично от р₁ и р₂. Состояния 1 и 2 лежат на одной изотерме. Поэтому в соответствии с (98.3) р₁V₁ = p'V₂. Состояния 1' и 2 лежат на одной изохоре. Следовательно, согласно (98.10) 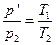. При исключении из этих уравнений величины р' получается объединенный газовый закон: 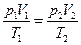. Состояния 1 и 2 были взяты произвольно, поэтому можно утверждать, что для любого состояния

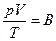(98.11)

где В – постоянная для данной массы газа величина. В соответствии с законом Авогадро, киломоли всех газов занимают при одинаковых условиях одинаковый объем. В частности, при так называемых нормальных условиях, т. е. при 0°С и давлении, равном 1 атм, объем киломоля любого газа равен 22,4 м³/кмоль^-1. Отсюда следует, что в случае, когда количество газа равно одному киломолю, величина В в (98.11) будет одинакова для всех газов. Обозначив соответствующую киломолю величину В буквой R, а объем киломоля V_км, уравнение (98.11) можно записать следующим образом:

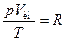(98.12)

Это уравнение называют уравнением Клапейрона. Оно связывает параметры киломоля идеального газа и, следовательно, представляет собой уравнение состояния идеального газа. Его обычно пишут в виде

pV_км = RT (98.13)

Величина R называется универсальной газовой постоянной. Ее значение можно вычислить на основании закона Авогадро, подставив в (98.12) р, равное 1,01×10⁵ н/м² (1 атм), V_км, равный 22,4 м³/кмоль, и Т, равную 273° К:

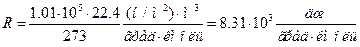
От уравнения для одного киломоля легко перейти к уравнению для любой массы газа m, приняв во внимание, что при одинаковых давлении и температуре z киломолей газа будут занимать в z раз больший объем, чем один киломоль: V = zV_км. Умножив (98.13) на z = m/m (m – масса газа, (m – масса киломоля) и заменив zV_км через V, получаем:

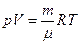(98.14)

Это и есть уравнение состояния идеального газа, написанное для произвольной массы газа m.

Простая связь между температурой и остальными параметрами идеального газа делает газ хорошим термометрическим веществом. При постоянстве объема и использовании в качестве температурного признака давления газа получается термометр с идеально линейной температурной шкалой (идеальная газовая шкала температур). В качестве термометрического тела берется водород. Установленная по водороду с использованием уравнения (98.14) шкала называется эмпирической шкалой температур.

Наибольших успехов достигла молекулярно-кинетическая теория в объяснении самого простого – газообразного – состояния вещества. Даже в своем наиболее элементарном виде, с использованием целого ряда упрощающих предположений, кинетической теории удается дать не только качественное, но и количественное (с точностью до числового множителя порядка единицы) объяснение основных свойств газообразного состояния и происходящих в газах явлений. Первая задача, которую имеет смысл рассмотреть – вычисление величины давления газа на стенки сосуда. Решение этой задачи прольет свет на физическую природу абсолютной температуры.

Дата добавления: 2015-05-09