Распределение Максвелла

Тепловая скорость u_T представляет собой некоторую среднюю характеристику теплового движения частиц. В действительности различные молекулы движутся с различными скоростями и можно поставить вопрос о распределении молекул по скоростям: сколько (в среднем) из имеющихся в теле молекул обладает теми или иными скоростями?

Легко решить этот вопрос для идеального газа, находящегося в состоянии теплового равновесия, причем столб газа испытывает действие однородного поля тяжести. В этом случае следует сначала интересоваться распределением молекул по значениям лишь одной (вертикальной) компоненты скорости u_z. Пусть величина

nf (u _z) d u _z

есть число молекул в 1 см³ газа, у которых значение этой компоненты лежит в бесконечно малом интервале между некоторым u_z и u_z ± du_z. Если n – полное число молекул в данном объеме, то функция f(u_z) определяет долю числа молекул с тем или иным значением u_z.

Можно подсчитать число молекул со скоростями в интервале du_z, находящихся в слое газа толщины dz на высоте z. Объем этого слоя совпадает с dz (если площадь сечения столба газа 1 см²), поэтому число рассматриваемых молекул равно

n (z) f (u _z)d u _z d z,

где n (z) – плотность газа на высоте z. Двигаясь как свободные (столкновения в идеальном газе уже учтены введением различных значений скоростей), эти молекулы с течением времени перейдут на некоторую другую высоту z ', заняв слой толщины d z ' и приобретя скорости в интервале между некоторым u '_z и u '_z ± d u '_z.

Неизменность числа этих молекул выражается равенством

n (z) f (u _z)d u _z d z = n (z ') f (u '_z)d u '_z d z '

При движении в поле тяжести горизонтальные составляющие скорости (u_x, u_y) не меняются, а изменение u _z определяется законом сохранения энергии:

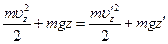
При заданных постоянных значениях z и z ' дифференцирование этого равенства дает соотношение

u _z d u _z = u '_z d u '_z

между интервалами d u _z и d u '_z, в которых заключены вертикальные скорости рассматриваемых молекул на высотах z и z '. Толщины же слоев d z и d z ' связаны друг с другом также соотношением

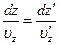
Оно выражает собой просто то обстоятельство, что за время d t =d z /u_z, в течение которого молекула пересекает слой dz на высоте z, на высоте z' она пройдет расстояние d z ' = u'_zdt.

Из полученных двух равенств получается

d u _zd z = d u '_zd z '.

Поэтому в написанном выше условии постоянства числа молекул дифференциалы в обеих сторонах равенства взаимно сокращаются:

n (z) f (u _z) = n (z ') f (u '_z)

С помощью барометрической формулы отсюда получается:

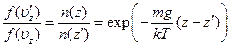
Из закона сохранения энергии

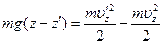
получается соотношение

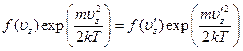
показывающее, что это произведение есть константа, не зависящая от u_z. Другими словами, функция f(u_z) имеет вид

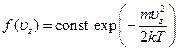
[Существенно, что ускорение силы тяжести в эту формулу не вошло. Так и должно быть, поскольку механизм установления распределения молекул газа по скоростям заключается в столкновениях молекул друг с другом и не имеет отношения к внешнему полю. Последнее играло в выводе лишь вспомогательную роль: введение этого поля, позволило связать распределение по скоростям с известной формулой Больцмана.]

Полученное равновесное распределение молекул по значениям одной отдельной компоненты их скорости позволяет найти долю молекул, обладающих определенными значениями всех трех компонент скорости одновременно. Она получится, очевидно, перемножением долей молекул, обладающих определенными значениями каждой из компонент в отдельности. Другими словами, полная функция распределения имеет вид

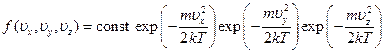
Так как 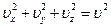, окончательно функция приобретает вид

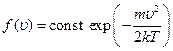
Таким образом, число dN молекул в газе, компоненты скорости которых лежат в интервалах между u_x, u_y, u_z и u_x +du_x, u_y +du_y, u_z +du_z, есть

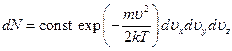
Здесь постоянный коэффициент const определяется тем условием, что полное число молекул со всеми возможными значениями скоростей равно заданному числу N молекул в газе. Полученная формула называется формулой распределения Максвелла.

Легко обнаружима аналогия между этой формулой и формулой Больцмана для распределения плотности газа по пространству во внешнем поле: в обоих случаях работает экспоненциальное выражение вида

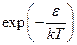
где e – энергия молекулы: кинетическая энергия mu²/2 в случае распределения по скоростям или потенциальная энергия U (x, у, z) во внешнем поле в случае распределения по пространству. Такое выражение часто называют больцмановским множителем.

Три компоненты u_x, u_y, u_z определяют скорость молекулы по ее направлению и по величине. Но распределение молекул по направлениям скорости просто равномерно – во всех направлениях летят в среднем одинаковые числа молекул. Это следует из распределения Максвелла, в котором фигурирует только абсолютная величина скорости u. Кроме того, если бы распределение скоростей по направлениям было неравномерным, то в газе существовало бы некоторое преимущественное направление движения молекул. При этом газ в целом не покоился бы, а двигался в этом направлении.

Формулу Максвелла следует преобразовать так, чтобы она прямо отвечала на вопрос о распределении молекул газа по абсолютным значениям скоростей, вне зависимости от их направления. Для этого надо просуммировать числа молекул, различающихся значениями компонент скорости u_x, u_y, u_z при одинаковой сумме 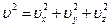. Это легко сделать, пользуясь следующим геометрическим приемом. Если ввести систему координат, на осях которой откладываются значения u_x, u_y, u_z, то произведение du_xdu_ydu_z будет представлять собой объем бесконечно малого параллелепипеда с длинами сторон du_x, du_y, du_z. Следует просуммировать все такие элементарные объемы, находящиеся на одинаковом расстоянии от начала координат (в этих координатах u представляет собой длину «радиуса-вектора»). Эти объемы заполнят шаровой слой между двумя бесконечно близкими сферами с радиусами u и u + du. Его объем равен произведению площади сферической поверхности 4pu² на толщину слоя du.

Таким образом, замена в формуле распределения Максвелла произведения du_xdu_ydu_z на 4pu²du, даст число молекул со скоростями в интервале значений между u и u + du:

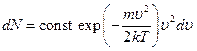
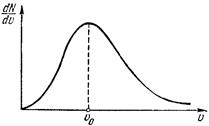
Выражение, стоящее в этой формуле перед du, представляет собой число молекул, отнесенное к единичному интервалу значений скорости. Как функция от u оно имеет вид, изображенный на рисунке. Оно равно нулю при u = 0, достигает максимума при

некотором u = u₀ и очень быстро стремится к нулю с дальнейшим возрастанием скорости. Максимум кривой соответствует значению 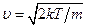, несколько меньшему, чем определенная выше тепловая скорость u_Т.

Поскольку разные молекулы имеют различные скорости, то при определении средних характеристик существенно, какая именно величина подвергается усреднению. Так, среднее значение первой степени скорости 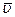отнюдь не совпадает со скоростью 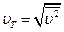(которую часто называют также средней квадратичной с целью подчеркнуть ее происхождение). С помощью распределения Максвелла можно показать, что .

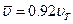Еще два замечания о распределении Максвелла.

1. Константа в распределении определяется из условия нормировки: число всех частиц, обладающих скоростями в диапазоне 0 < u < ¥, то есть всех рассмотренных при выводе частиц, равно N. Получение константы в распределении связано с вычислением нестандартного интеграла, поэтому конечное выражение для распределения дается без вывода:

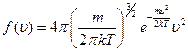
2. В следующей таблице приведены соответствующие относительные количества молекул Δ N / N для различных интервалов скоростей. Эти значения позволяют достаточно хорошо представить вероятность существования частиц, обладающих скоростью даже весьма скромно отличающихся от наиболее вероятной.

Таблица

u / u вер	Δ N / N, %	u / u вер	Δ N / N, %
0 – 0.5	8.1	2 – 3	4.6
0.5 – 1.5	70.7	> 3	0.04
1.5 – 2.0	16.6	> 5	8×10^-9

Из таблицы видно, что более чем у 70% всех молекул скорость отличается от наиболее вероятной не больше чем на 50%. Скоростью u > 3 u _вер обладает в среднем только 0,04% молекул. Скорости же более 5 u _вер наблюдаются в среднем лишь у одной из 12 миллиардов молекул.

Распределение Максвелла, выведенное здесь для одноатомного газа, может быть в действительности получено из гораздо более общих теоретических соображений и имеет универсальный характер. Оно справедливо для теплового движения молекул и атомов в любых телах. Следует, однако, подчеркнуть, что распределение Максвелла основано на классической механике. Поэтому его справедливость в такой же мере ограничена квантовыми явлениями, как и вообще применимость классической механики к тепловому движению.

Экспериментальное подтверждение распределения скоростей теплового движения было проведено различными методами, использующими молекулярные пучки. Последние получаются выпусканием в откачанную камеру молекул, испаряющихся с нагреваемого в специальной печке вещества. При этом камера откачивается до такого вакуума, чтобы молекулы летели в ней, практически не испытывая столкновений. Один из таких методов

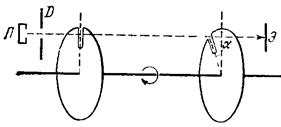
основан на идее механического селектора скоростей. В откачанном пространстве вращаются насаженные на общую ось (на расстоянии l) два круговых диска с радиальными прорезями, смещенными друг относительно друга на некоторый угол a (см. рисунок). На эти диски направляется из печки П через диафрагму D молекулярный пучок. Молекула, проходящая через прорезь в первом диске со скоростью u, достигает второго диска через время t = l / u. За это время диск повернется на угол Ωt = Ω l / u, где Ω – угловая скорость вращения. Поэтому пройдут через прорезь во втором диске и оставят след на экране Э лишь молекулы со скоростью, удовлетворяющей равенству Ω l / u = a. Меняя скорость вращения дисков и измеряя плотность налета на экране, можно тем самым определить отношение чисел частиц с различными скоростями.

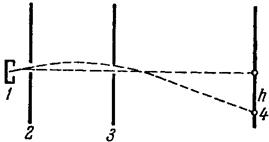
Экспериментальная проверка распределения Максвелла была осуществлена также путем наблюдения отклонения молекулярного пучка в поле тяжести. Атомы цезия, нагреваемого в печке 1 и вылетающие из отверстия в ней, попадают в откачанную камеру. Узкий пучок, выделяемый диафрагмами 2 и 3, отклоняется вниз полем тяжести и улавливается детектором – горизонтальной горячей вольфрамовой тонкой проволочкой 4, которую можно располагать на различных расстояниях h ниже оси прибора (атомы цезия, попадая на проволочку, покидают ее снова в виде положительных ионов, собираемых отрицательно заряженной пластинкой). Отклонение h атома зависит от его скорости u (оно составляло в опытах десятые доли миллиметра при длине пути пучка в 2м). Измерение интенсивности пучка на различных расстояниях h дает распределение атомов в пучке по скоростям.

Дата добавления: 2015-05-09