Уравнение движения

Уравнения движения можно вывести с помощью теоремы о количестве движения, примененной к сплошной движущейся среде.

Пусть произвольная фиксированная замкнутая поверхность S ограничивает объем V. Применим к жидкости, протекающей через этот объем, закон количества движения: скорость изменения ко­личества движения, возникающего внутри объема, равна дей­ствующей на объем силе.

Найдем сначала скорость изменения количества движения жидкости в выделенном объеме.

Обозначим n_iвектор единичной нормали к поверхности S (см. рис. 2.1). Тогда масса жидкости, вытекающая в единицу времени через элемент поверхности, как и ранее, равна ru_in_ids. Вытекающая масса выносит из объема некоторое количество дви­жения, которое является векторной величиной и может быть найдено умножением массы на вектор скорости ru_iu_jn_ids. Это выражение представляет собой количество движения, вынесенное из объема через элемент поверхности в единицу времени (в проек­ции на ось у). Следовательно, через всю поверхность выносится количество движения,

равное 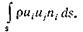(2.12)

Количество движения жидкости, заключенной в объеме, может изменяться также вследствие изменения скорости и плотности жидкости внутри объема во времени. Это изменение представляется интегралом по объему 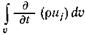(2.13)

Сумма выражений (2.12) и (2.13) дает полную скорость изме­нения количества движения выделенного объема жидкости и должна быть равна действующей на объем силе 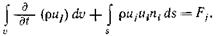(2.14)

Под f_j следует понимать результирующую всех сил, прило­женных к жидкости в выделенном объеме. Все члены этого уравне­ния имеют один и тот же свободный индекс j, так как изменение количества движения и сила должны проектироваться на одну и ту же ось координат.

Силы, действующие на жидкость, можно подразделить на массовые и поверхностные. Силы, действующие на единицу массы жидкости, обозначим f_j — это может быть сила тяжести или сила электромагнитного происхождения, возникающая в токопроводящей жидкости.

Тогда полная массовая сила, действующая на выделенный объем жидкости, равна 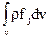(2.15)

Поверхностными называются силы, действующие только на поверхность жидкости выделенного объема со стороны окружа­ющей жидкости. Эти силы в общем случае действуют как по нор­малям, так и по касательным к поверхности. Эти силы, как пока­зано в разд. 1.3, представляются напряжениями σ_ij. В данном случае необходимо найти напряжения на площадке, которой соответствует нормаль n_i.

Согласно формуле (1.14) напряжения на такой площадке равны п_i σ_ij(напомним, что второй индекс у σ означает ось проек­тирования).

Следовательно, проекция на ось j полной силы, действующей на выделенную поверхность, равна

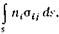(2.16)

Заменив F_j – в уравнении (2.14) через сумму выражений (2.15) и (2.16), получим уравнение движения в интегральной форме 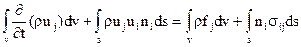(2.17)

Для того чтобы получить уравнение движения в дифферен­циальной форме, необходимо, как и при выводе уравнения нераз­рывности, заменить интегралы по поверхности интегралами по объему с помощью формулы Гаусса — Остроградского (2.6, 2.7):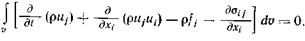

Полученное выражение справедливо для произвольного объ­ема v, поэтому подынтегральное выражение должно быть равно нулю. Отсюда получаем уравнение движения в дифференциальной форме 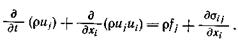(2.18)

Это уравнение можно упростить, если продифференцировать произведения, стоящие в скобках, 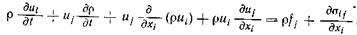и заметить, что сумма второго и третьего членов равна нулю в силу уравнения неразрывности (2.9).

Тогда получим 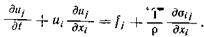(2.19)

B этом уравнении целесообразно явно выделить член, завися­щий от давления, воспользовавшись представлением напряжений по формуле * (1.13): (2.20)

Для жидкости, лишенной вязкости (идеальная жидкость), последний член уравнения равен нулю и оно переходит в уравне­ние, полученное Эйлером, 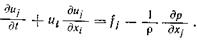(2.21)

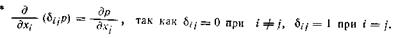
Дата добавления: 2015-05-09