Уравнение энергии. Третье основное уравнение гидроаэромеханики представляет запись уравнения энергии

Третье основное уравнение гидроаэромеханики представляет запись уравнения энергии. При движении жидкости поверхностные и массовые силы совершают работу. К жидкости может подводиться теплота. Вследствие этого может изменяться как кинетическая, так и внутренняя энергия жидкости.

Рассмотрим опять замкнутую поверхность s, окружающую объем υ, и составим баланс энергий для текущей жидкости. Энергию, отнесенную к единице объема жидкости, можно записать как сумму кинетической и внутренней энергий (энергия — скалярная величина, и поэтому полученное выражение не имеет индексов) 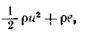где u² = u_iu_i = u₂₁ + u₂₂ + u₂₃ – квадрат модуля вектора скорости; е — внутренняя энергия единицы массы жидкости.

Тогда скорость изменения энергии жидкости,

заключенной в фиксированном объеме, равна 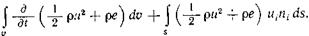(2.22)

Первый интеграл выражает скорость изменения энергии внутри объема в результате изменения параметров потока (скорости, плотности и т. д.) во времени при неустановившемся движении. Второй интеграл представляет скорость выноса энергии из объема текущей жидкостью. Следовательно, сумма интегралов равна скорости «появления» энергии внутри объема. Источником этой энергии служит работа, производимая в единицу времени массо­выми и поверхностными силами, а также подводимая к объему теплота. Работа в единицу времени равна мощности. Мощность можно представить как скалярное произведение векторов силы и скорости или в индексной записи произведением F_iu_i.

Массовые силы развивают внутри объема мощность, равную 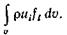(2.23)

Поверхностная сила, действующая на элемент поверхности, равна (проекция на j-ю ось) σ_ij n_ids. Следовательно, чтобы полу­чить мощность, развиваемую этими силами, надо помножить это выражение на и_j — проекцию скорости на j-ю ось. Тогда полная мощность поверхностных сил представится интегралом по поверх­ности 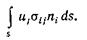(2.24)

Рассмотрим теперь подвод теплоты к выделенному объему. Теплота может подводиться к выделенному объему жидкости благодаря внутренним источникам, например, при конденсации, горении и т. п. Обозначим q скорость подвода теплоты к единице массы жидкости благодаря внутренним источникам. Тогда ско­рость подвода теплоты к выделенному объему жидкости равна 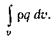(2.25)

Теплота может подводиться к жидкости данного объема также извне, т. е. от окружающей жидкости. Обозначим Q _i вектор по­тока теплоты через единицу площади в единицу времени. Тогда скорость передачи теплоты через элемент поверхности из объема наружу равна Q_in_i ds (η_i — внешняя единичная нормаль к поверх­ности). Передача теплоты через поверхность происходит вследствие теплопроводности жидкости, и тогда вектор Q_i, можно выразить через градиент температурного поля и коэффициент теплопро­водности c: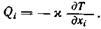

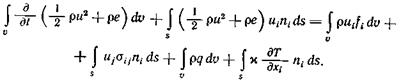Следовательно, скорость подвода теплоты к объему (знак плюс) можно представить интегралом по поверхности 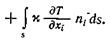(2.26)

Сумма выражений (2.23)—(2.26) представляет скорость подвода энергии к жидкости в фиксированном объеме. На основании закона сохранения энергии эта сумма равна скорости изменения энергии жидкости в объеме, определяемой выражением (2.22). Следовательно, уравнение энергии в интегральной форме имеет вид (2.27)

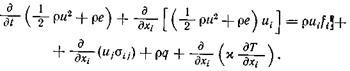Заменив интегралы по поверхности интегралами по объему с помощью формулы Гаусса — Остроградского точно так же, как это было сделано в разд. 2.1, 2.2, получим уравнение энергии в дифференциальной форме (2.28)

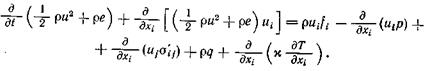Воспользовавшись формулой (1.13), запишем уравнение (2.28), выделив отдельно члены, которые учитывают работу сил давления и работу сил вязкости (2.29)

Заметим, что здесь все индексы немые, т. е. исчезают при сумми­ровании, так как уравнение энергии является скалярным.

Возможные упрощения уравнения энергии (2.29) для отдель­ных частных случаев, когда, например, можно пренебречь тепло­обменом или работой сил вязкости и т. д., очевидны.

Рассмотрим подробнее случай движения идеальной жидкости (вязкость равна нулю). Пренебрежем также теплообменом и рабо­той сил тяжести. В газовой динамике обычно можно пренебрегать влиянием силы тяжести, так как движение происходит в относительно малом пространстве и с большими скоростями. В этом случае работа сил тяжести пренебрежимо мала.

Тогда уравнение энергии (2.29) примет вид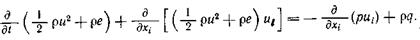

(2.30)

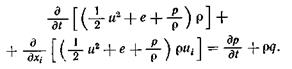Сгруппируем второй и третий члены и добавим к обеим частям уравнения член dp/dt

Можно ввести энтальпию по формуле

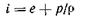
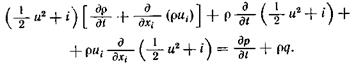и записать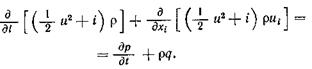

Продифференцировав произведения, стоящие в квадратных скоб­ках, получим

Заметив, что выражение, стоящее в квадратных скобках, равно нулю на основании уравнения неразрывности (2.9), получим окончательную запись уравнения энергии для данного частного случая

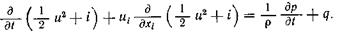(2.32)

Отсюда следует, что для идеальной жидкости величина 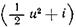может изменяться вследствие подвода теплоты или изменения давления во времени. Если приток тепла отсутствует, а движение установившееся, то уравнение энергии принимает вид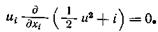

Это означает, что энергия частицы жидкости во время движения остается постоянной. Действительно, если направить одну из осей координат (например x₁) вдоль скорости, то и₁ = и, u ₂ = u₃ = 0 и, следовательно, 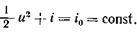(2.33)

Линия, касательная к которой в любой точке совпадает с напра­влением скорости, называется линией тока. В установившемся движении линия тока совпадает с траекторией движения частицы. Следовательно, в данном случае все частицы, движущиеся вдоль одной линии тока, обладают одинаковой и постоянной энергией. Постоянная может быть и различной для различных линий тока.

Дата добавления: 2015-05-09