
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
По определению байесовского решающего правила получаем, что 1 страница
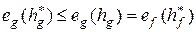 .
.
Из доказанной теоремы следует, что байесовская классификация с использованием расширенного набора признаков не увеличивает вероятность ошибки, соответствующей исходному набору. С другой стороны, расширение набора признаков не всегда приводит к желаемому снижению вероятности ошибки, достигнутой для исходного набора. В таких случаях добавленные признаки естественно назвать бесполезными, а их выбор признать неудачным. Проиллюстрируем сказанное на следующем примере.
Рассмотрим классификацию пикселей на два класса 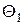 и
и 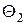 . Пусть
. Пусть 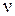 - размерность признакового пространства,
- размерность признакового пространства, 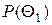 и
и 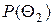 - априорные вероятности, а
- априорные вероятности, а 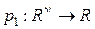 и
и 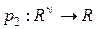 - непрерывные плотности распределений признаков классов. Из теоремы Байеса [39, с. 27] следует, что решающее правило
- непрерывные плотности распределений признаков классов. Из теоремы Байеса [39, с. 27] следует, что решающее правило 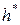 , определенное равенством
, определенное равенством
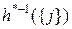 =
=  ,
, 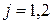 ,
,
является байесовским (имеет наименьшую вероятность ошибки).
Пусть 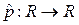 - непрерывная плотность вероятностей в
- непрерывная плотность вероятностей в 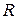 . Очевидно, что отображения
. Очевидно, что отображения 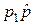 и
и 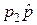 так же будут плотностями вероятностей, но уже в
так же будут плотностями вероятностей, но уже в 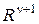 . В соответствии с введенным выше определением, их можно рассматривать в качестве плотностей распределений расширенных наборов признаков тех же классов
. В соответствии с введенным выше определением, их можно рассматривать в качестве плотностей распределений расширенных наборов признаков тех же классов 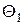 и
и 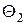 . Если
. Если 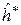 - байесовское решающее правило в признаковом пространстве
- байесовское решающее правило в признаковом пространстве 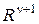 , то оно разбивает
, то оно разбивает 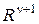 на две части
на две части 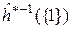 и
и 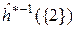 , определяемые равенствами
, определяемые равенствами
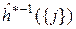 =
= 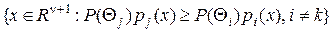 =
=
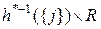 ,
, 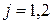 .
.
Из этого следует, что
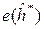 =
= 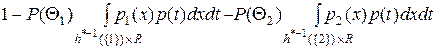 =
=
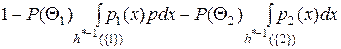 =
= 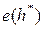 .
.
Что и требовалось доказать.
Полученный результат допускает естественную интерпретацию в случае, когда в качестве признаков используются энергетические яркости, зарегистрированные в различных спектральных зонах оптического диапазона, включая зону [0.38;0.78] мкм. Известно, что в этой спектральной зоне, называемой часто видимой, при обычных температурах собственное излучение тел, практически, отсутствует. Поэтому при съемке без освещения (например, в темное время суток) изображением сцены в этой спектральной зоне будет набор случайных яркостей, обусловленных собственными шумами оптико-электронной системы. Очевидно, что никакой информации о сцене такое изображение не содержит.
С другой стороны, пусть для классификации пикселей на два класса используется единственный признак. Предположим, что в каждом классе он имеет нормальное распределение с параметрами ( ) и (
) и (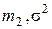 ) соответственно. Показано (см., например, [39]), что при одинаковых априорных вероятностях классов вероятность байесовской ошибки принимает вид
) соответственно. Показано (см., например, [39]), что при одинаковых априорных вероятностях классов вероятность байесовской ошибки принимает вид
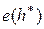 =
= 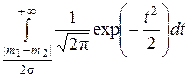
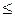
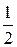 .
.
Очевидно, что она убывает с ростом отношения сигнал/шум 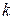
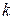 =
= 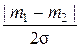 .
.
Поэтому 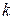 будет использоваться далее для оценки качества (информативности) изображения даже в тех случаях, когда предположения о равенстве априорных вероятностей и нормальном виде распределений классов не выполняются.
будет использоваться далее для оценки качества (информативности) изображения даже в тех случаях, когда предположения о равенстве априорных вероятностей и нормальном виде распределений классов не выполняются.
Пусть теперь для классификации на два класса используется набор из 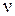 независимых признаков. Предположим, что в
независимых признаков. Предположим, что в 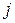 -ом классе,
-ом классе, 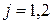 , признаки имеют многомерное нормальное распределение с вектором средних значений
, признаки имеют многомерное нормальное распределение с вектором средних значений 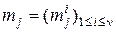 и матрицей ковариаций
и матрицей ковариаций 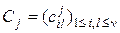 вида
вида 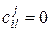 при
при 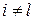 и
и 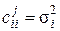 . Определим для каждого признака отношение сигнал/шум
. Определим для каждого признака отношение сигнал/шум 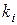 равенством
равенством
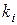 =
= 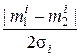 ,
, 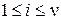 .
.
Показано [39], что при одинаковых априорных вероятностях классов вероятность 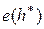 байесовской ошибки принимает вид
байесовской ошибки принимает вид
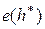 =
= 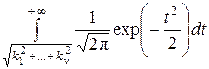
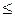
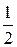 .
.
Очевидно, что с увеличением 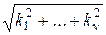 вероятность ошибки классификации убывает.
вероятность ошибки классификации убывает.
В частном случае, если в каждом классе признаки имеют одно и то же нормальное распределение с параметрами 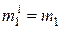 ,
, 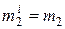 и
и 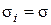 ,
, 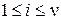 , то вероятность ошибки принимает вид
, то вероятность ошибки принимает вид
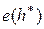 =
= 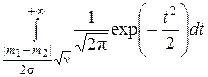
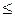
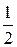 .
.
Из него следует, что для снижения вероятности ошибки классификации существует два способа. В самом деле, увеличение в 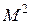 раз количества спектральных зон (скалярных компонент) дает такой же эффект, что и применение единственного признака, параметры (
раз количества спектральных зон (скалярных компонент) дает такой же эффект, что и применение единственного признака, параметры (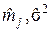 ) которого удовлетворяют равенству
) которого удовлетворяют равенству
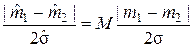 .
.
Следует иметь в виду, что для измерения (регистрации) нового признака может потребоваться разработка технических средств, использующих принципиально иные физические принципы.
Довольно часто для снижения вероятности ошибки классификации возникает сооблазн в замене имеющегося набора 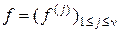 из
из 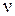 признаков другим набором, состоящим из такого же количества признаков. В приводимом ниже утверждении формулируются условия, при выполнении которых вероятность ошибки классификации с применением нового набора остается прежней.
признаков другим набором, состоящим из такого же количества признаков. В приводимом ниже утверждении формулируются условия, при выполнении которых вероятность ошибки классификации с применением нового набора остается прежней.
Теорема 3.2.2. Пусть 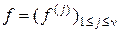 - некоторый набор признаков, а
- некоторый набор признаков, а 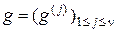 - взаимно однозначное отображение вида
- взаимно однозначное отображение вида 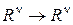 , задаваемое
, задаваемое 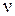 гладкими отображениями
гладкими отображениями 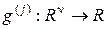 . Тогда суперпозиция
. Тогда суперпозиция 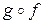 также является набором признаков. Более того, если
также является набором признаков. Более того, если 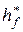 и
и 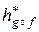 - байесовские решающие правила для
- байесовские решающие правила для 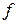 и
и 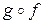 соответственно, то
соответственно, то 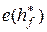 =
= 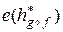 .
.
Следствие. Если 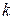 и
и 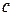 - константы, то из доказанной теоремы следует, что признаки
- константы, то из доказанной теоремы следует, что признаки 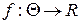 и
и 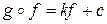 имеют одну и ту же байесовскую вероятность ошибки.
имеют одну и ту же байесовскую вероятность ошибки.
3.3 Объединение классов
Пусть 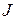 - конечное множество индексов, содержащее не менее трех элементов,
- конечное множество индексов, содержащее не менее трех элементов, 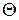 - множество объектов,
- множество объектов, 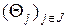 - его разбиение на
- его разбиение на 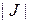 классов, которое будет называться далее исходным. Объединяя некоторые из классов исходного разбиения, можно получить другое разбиение, состоящее из меньшего числа классов. Это разбиение естественно назвать более грубым по сравнению с исходным. Рассмотрим вопрос о вероятностях ошибок классификации, соответствующих исходному и полученному из него более грубому разбиению.
классов, которое будет называться далее исходным. Объединяя некоторые из классов исходного разбиения, можно получить другое разбиение, состоящее из меньшего числа классов. Это разбиение естественно назвать более грубым по сравнению с исходным. Рассмотрим вопрос о вероятностях ошибок классификации, соответствующих исходному и полученному из него более грубому разбиению.
Пусть 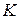 - множество индексов такое, что
- множество индексов такое, что 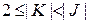 , и пусть
, и пусть 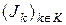 - разбиение исходного множества индексов
- разбиение исходного множества индексов 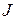 на
на  подмножеств. Для каждого
подмножеств. Для каждого 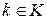 построим множество
построим множество 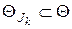 следующим образом
следующим образом
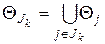 .
.
Из определения семейства 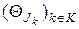 следует, что оно является разбиением
следует, что оно является разбиением 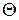 на классы более грубым, чем исходное разбиение
на классы более грубым, чем исходное разбиение 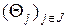 .
.
Если 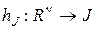 - решающее правило классификации объектов
- решающее правило классификации объектов 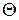 на
на 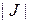 классов, то из его определения следует, что
классов, то из его определения следует, что
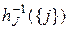 =
= 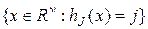
и что
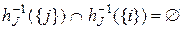 ,
, 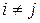 , а
, а 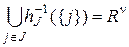 .
.
Определим для каждого 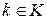 подмножество
подмножество 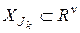 при помощи равенства
при помощи равенства
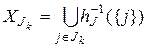 .
.
По построению, 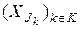 - разбиение на
- разбиение на 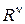 . Поэтому отображение
. Поэтому отображение 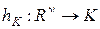 , определяемое равенством
, определяемое равенством
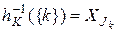 ,
,
является решающим правилом для классификации объектов 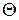 на
на  новых классов
новых классов 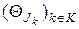 . В связи с этим будем говорить, что правило
. В связи с этим будем говорить, что правило  порождает более грубое правило
порождает более грубое правило 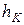 . Можно доказать следующий результат [51-52].
. Можно доказать следующий результат [51-52].
Теорема 3.3.1. Пусть 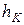 - решающее правило, порожденное решающим правилом
- решающее правило, порожденное решающим правилом  . Если
. Если 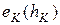 и
и 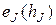 - соответствующие им вероятности ошибок классификации, то
- соответствующие им вероятности ошибок классификации, то 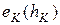
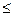
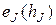 .
.
Лемма 3.3.2. Для того, чтобы отображение 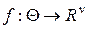 было случайной величиной на
было случайной величиной на 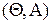 , необходимо и достаточно, чтобы каждое сужение
, необходимо и достаточно, чтобы каждое сужение 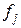 ,
, 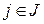 , было случайной величиной на соответствующем измеримом подпространстве
, было случайной величиной на соответствующем измеримом подпространстве 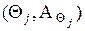 .
.
Лемма 3.3.3. Для любого решающего правила 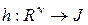 подмножество
подмножество 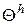 объектов из
объектов из 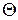 , классифицируемых с ошибкой, является событием из
, классифицируемых с ошибкой, является событием из 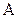 и имеет вероятность
и имеет вероятность
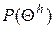 =
= 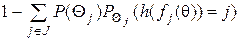 .
.
3.4 Свойства пятен на локально однородных сценах
Пусть 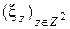 - локально однородная сцена, а
- локально однородная сцена, а 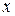 - ее изображение. Покажем, что для такой сцены имеет место следующий результат.
- ее изображение. Покажем, что для такой сцены имеет место следующий результат.
Теорема 3.4.1. Пусть 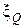 - зона интереса на локально однородной сцене, содержащая светлое пятно
- зона интереса на локально однородной сцене, содержащая светлое пятно 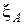 и его фон
и его фон 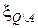 . Пусть
. Пусть 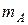 и
и 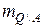 - средние значения объекта и фона, а
- средние значения объекта и фона, а  - изображение квадрата. Если
- изображение квадрата. Если 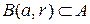 и
и 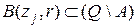 ,
, 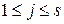 , - попарно не пересекающиеся квадратные окрестности, состоящие из
, - попарно не пересекающиеся квадратные окрестности, состоящие из 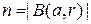 точек каждая, а
точек каждая, а
 и
и 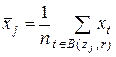 ,
, 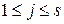 ,
,
то при любом фиксированном 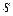
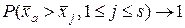 при
при 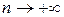 .
.
Замечание 1. Из предложенного доказательства не следует, что сходимость 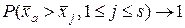 является равномерной по
является равномерной по 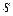 .
.
Замечание 2. В доказательстве теоремы используется предельный переход при стремлении к бесконечности числа 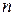 пикселей окрестности или, что эквивалентно, ее радиуса
пикселей окрестности или, что эквивалентно, ее радиуса 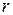 . По условиям Теоремы окрестность
. По условиям Теоремы окрестность 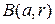 должна принадлежать конечному множеству (проекции)
должна принадлежать конечному множеству (проекции) 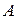 , а окрестности
, а окрестности 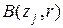 ,
, 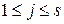 , - конечному множеству
, - конечному множеству 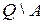 . Поэтому предельный переход в этих условиях является, строго говоря, незаконной операцией. Однако ситуацию легко исправить, если заменить изображения
. Поэтому предельный переход в этих условиях является, строго говоря, незаконной операцией. Однако ситуацию легко исправить, если заменить изображения 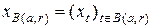 и
и 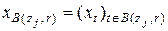 ,
, 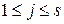 , окрестностей на стационарные случайные последовательности
, окрестностей на стационарные случайные последовательности 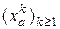 и
и 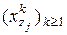 со средними значениями
со средними значениями 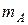 и
и 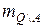 , для которых выполняются условия Теоремы Слуцкого, и определить
, для которых выполняются условия Теоремы Слуцкого, и определить 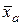 и
и 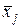 при помощи равенств
при помощи равенств
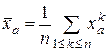 и
и 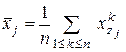 ,
, 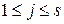 .
.
При решении прикладных задач вместо пределов используются их приближенные значения 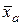 и
и 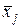 ,
, 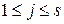 . Они являются суммами конечного числа слагаемых и вычисляются по
. Они являются суммами конечного числа слагаемых и вычисляются по 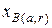 и
и  ,
, 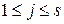 , при конечном радиусе
, при конечном радиусе 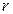 . Поэтому и далее при формулировке и доказательстве теорем, аналогичных Теореме 3.4.1, для наглядности будут использоваться окрестности, состоящие из конечного числа пикселей, а не последовательности.
. Поэтому и далее при формулировке и доказательстве теорем, аналогичных Теореме 3.4.1, для наглядности будут использоваться окрестности, состоящие из конечного числа пикселей, а не последовательности.
Доказанная теорема указывает на важное свойство (признак) пикселей, образующих пятно 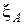 . В самом деле, при достаточно больших значениях
. В самом деле, при достаточно больших значениях 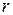 практически для всех изображений
практически для всех изображений 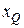 зоны интереса, содержащей светлое пятно, должны одновременно выполняться неравенства
зоны интереса, содержащей светлое пятно, должны одновременно выполняться неравенства 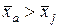 ,
, 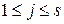 . Посмотрим, в какой степени это свойство зоны интереса характерно для квадрата
. Посмотрим, в какой степени это свойство зоны интереса характерно для квадрата 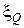 , образованного пикселями фона. Он не является зоной интереса. Предварительно докажем следующий результат.
, образованного пикселями фона. Он не является зоной интереса. Предварительно докажем следующий результат.
Теорема 3.4.2. Пусть 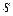 - натуральное число, а
- натуральное число, а 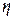 и
и 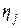 ,
, 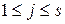 , - независимые в совокупности и одинаково распределенные дискретные случайные величины со значениями из множества
, - независимые в совокупности и одинаково распределенные дискретные случайные величины со значениями из множества 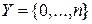 , средним значением
, средним значением 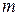 и среднеквадратичным отклонением
и среднеквадратичным отклонением 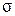 . Тогда
. Тогда
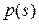 =
= 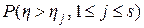 =
= 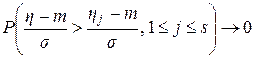 при
при 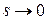 .
.
Для сравнения приближенные значения 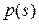 для нормально распределенных случайных величин
для нормально распределенных случайных величин 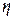 и
и 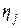 ,
, 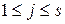 , рассчитанные методом Монте-Карло для
, рассчитанные методом Монте-Карло для 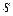 =1,…,30, приведены в таблице 3.1. Из приведенных
=1,…,30, приведены в таблице 3.1. Из приведенных
Таблица 3.1 - Значения вероятности 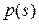 для случайных величин с нормальным законом распределения
для случайных величин с нормальным законом распределения
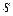
| ||||||||||
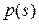
| 0.495 | 0.336 | 0.260 | 0.194 | 0.168 | 0.146 | 0.129 | 0.108 | 0.099 | 0.089 |
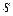
| ||||||||||
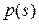
| 0.083 | 0.078 | 0.071 | 0.064 | 0.063 | 0.058 | 0.055 | 0.052 | 0.047 | 0.048 |
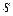
| ||||||||||
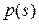
| 0.046 | 0.043 | 0.041 | 0.041 | 0.038 | 0.037 | 0.035 | 0.035 | 0.033 | 0.032 |
данных следует, что при увеличении 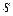 от 1 до 10 вероятность
от 1 до 10 вероятность 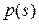 убывает более, чем в 5 раз. При дальнейшем увеличении
убывает более, чем в 5 раз. При дальнейшем увеличении 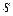 скорость убывания
скорость убывания 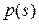 заметно замедляется.
заметно замедляется.
В 2.3 показано, что сцена 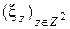 , полученная скользящим суммированием по квадратной окрестности с радиусом
, полученная скользящим суммированием по квадратной окрестности с радиусом 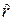 , из сцены
, из сцены 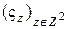 , состоящей из независимых в совокупности случайных величин с одним и тем
, состоящей из независимых в совокупности случайных величин с одним и тем
же распределением, является однородной. Для таких сцен имеет место следующий результат.
Теорема 3.4.3. Пусть 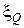 - квадрат на сцене, полученной скользящим суммированием по квадратной окрестности с радиусом
- квадрат на сцене, полученной скользящим суммированием по квадратной окрестности с радиусом 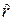 , и пусть
, и пусть  - его изображение. Если
- его изображение. Если 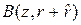 и
и 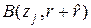 ,
, 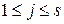 , - попарно не пересекающиеся квадратные окрестности из
, - попарно не пересекающиеся квадратные окрестности из 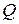 ,
, 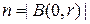 , а
, а 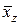 и
и 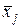 определяются равенствами
определяются равенствами
|
|
Дата добавления: 2015-05-09; Просмотров: 306; Нарушение авторских прав?; Мы поможем в написании вашей работы!