
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
По определению байесовского решающего правила получаем, что 2 страница
|
|
|
|
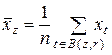 и
и 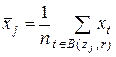 ,
, 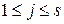 ,
,
то 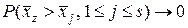 при
при 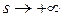 .
.
Доказанная теорема указывает на важное свойство (признак) пикселей, образующих фон 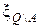 объекта
объекта 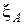 . В самом деле, если окрестности
. В самом деле, если окрестности 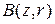 и
и 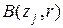 ,
, 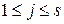 , принадлежат
, принадлежат 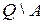 , то при достаточно больших значениях
, то при достаточно больших значениях 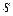 практически для всех изображений
практически для всех изображений 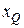 зоны интереса событие
зоны интереса событие 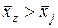 ,
, 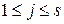 , является невозможным. Далее среднее арифметическое значение
, является невозможным. Далее среднее арифметическое значение 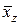 будет использоваться в качестве признака пикселя
будет использоваться в качестве признака пикселя  при поиске зон интереса и классификации их пикселей.
при поиске зон интереса и классификации их пикселей.
Очевидно, что все доказанные результаты справедливы также для бернуллиевских сцен.
3.6 Описание формы
Обозначения, используемые в настоящем пункте, имеют локальный характер. За его пределами они могут иметь другое значение.
При визуальном дешифрировании изображений форма присутствующих на сцене объектов является важным демаскирующим признаком. Однако применение этого признака при автоматическом дешифрировании наталкивается на серьезные трудности, связанные с отсутствием его удобной формализации. Поэтому, несмотря на довольно большое число публикаций, посвященных изложению различных способов определения (формализации) формы (см., например [49, 50, 69-71]), исследования в этом направлении, по-прежнему, сохраняют свою актуальность.
В настоящем пункте предлагается определение формы для ограниченных подмножеств 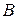 вещественной плоскости
вещественной плоскости 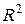 . Множества задаются замкнутыми спрямляемыми кривыми
. Множества задаются замкнутыми спрямляемыми кривыми  , которые описываются уравнениями вида
, которые описываются уравнениями вида 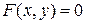 . Предполагается, что кривые не имеют кратных точек и что функция
. Предполагается, что кривые не имеют кратных точек и что функция 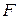 непрерывна. Далее подмножества
непрерывна. Далее подмножества 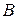 называются фигурами, а кривые
называются фигурами, а кривые  - их границами.
- их границами.
Независимо от используемого подхода, определение формы должно удовлетворять ряду очевидных требований. В частности, фигуры, получающиеся из исходной путем ее параллельного переноса (сдвига) или ее поворота относительно выбранной точки, должны иметь одинаковую форму. Эти преобразования образуют, как известно, группу движений на 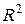 .
.
|
|
|
Пусть  - граница выпуклой фигуры
- граница выпуклой фигуры 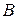 , а
, а 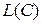 - ее длина. Зафиксируем на
- ее длина. Зафиксируем на  некоторую точку
некоторую точку 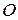 в качестве начала отсчета и зададим положительное направление. Это позволяет установить между точками кривой
в качестве начала отсчета и зададим положительное направление. Это позволяет установить между точками кривой  и точками отрезка
и точками отрезка 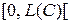 прямой взаимно однозначное соответствие. Точке
прямой взаимно однозначное соответствие. Точке 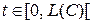 ставится в соответствие точка
ставится в соответствие точка 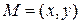 на
на  , находящаяся от
, находящаяся от 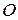 на расстоянии
на расстоянии 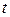 . Очевидно, что существуют отображения
. Очевидно, что существуют отображения 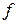 и
и 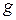 на
на 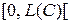 такие, что
такие, что 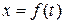 и
и 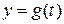 . Продолжим эти отображения на оставшуюся часть прямой при помощи равенств
. Продолжим эти отображения на оставшуюся часть прямой при помощи равенств 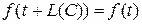 и
и 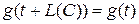 , то есть будем считать
, то есть будем считать 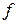 и
и 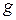 периодическими. Поскольку речь идет об ограниченных фигурах, то существуют
периодическими. Поскольку речь идет об ограниченных фигурах, то существуют 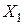 и
и 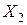 ,
, 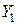 и
и 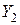 такие, что
такие, что 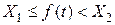 ,
, 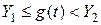 .
.
Далее будет предполагаться, что 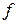 и
и 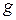 являются борелевскими. В связи с этим желательно указать класс фигур, для которых подобное предположение выполняется. Прежде всего, сошлемся на хорошо известный результат, в соответствии с которым все непрерывные функции являются борелевскими. В важном частном случае, когда множество
являются борелевскими. В связи с этим желательно указать класс фигур, для которых подобное предположение выполняется. Прежде всего, сошлемся на хорошо известный результат, в соответствии с которым все непрерывные функции являются борелевскими. В важном частном случае, когда множество 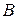 является многоугольником, доказать непрерывность функций
является многоугольником, доказать непрерывность функций 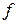 и
и 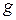 можно непосредственно.
можно непосредственно.
В самом деле, пусть 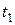 и
и 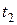 - точки из
- точки из 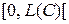 , соответствующие концам
, соответствующие концам 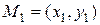 и
и 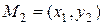 отрезка ломаной, принадлежащего прямой
отрезка ломаной, принадлежащего прямой 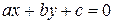 . Без ограничения общности будем считать, что
. Без ограничения общности будем считать, что 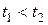 и что
и что 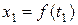 <
< 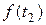
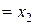 . Если
. Если 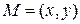 - точка на отрезке ломаной
- точка на отрезке ломаной  , соответствующая точке
, соответствующая точке 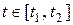 , то при
, то при 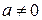 и
и 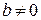 легко показать, что
легко показать, что
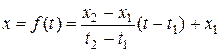 ,
, 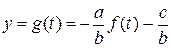 .
.
То есть, 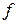 и
и 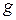 - непрерывные функции. Если
- непрерывные функции. Если 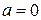 ,
, 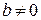 , то
, то
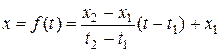 ,
, 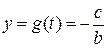 .
.
При 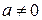 и
и 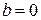 , по аналогии с предыдущим случаем, получаем, что
, по аналогии с предыдущим случаем, получаем, что
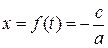 ,
, 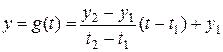 .
.
То есть, отображения 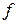 и
и 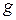 непрерывны.
непрерывны.
Известно, что отображение 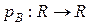 вида
вида
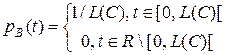 ,
,
является плотностью равномерно распределенной на 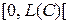 случайной величины
случайной величины  , определяемой равенством
, определяемой равенством 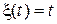 . Будем называть ее далее случайной точкой.
. Будем называть ее далее случайной точкой.
Каждой паре 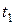 ,
, 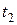 случайных точек на
случайных точек на 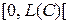 соответствует пара
соответствует пара 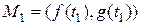 ,
, 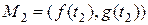 точек на кривой
точек на кривой 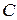 . По предположению,
. По предположению, 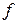 и
и 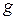 - борелевские функции, поэтому координаты точек
- борелевские функции, поэтому координаты точек  и
и 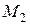 являются случайными величинами. Каждая пара
являются случайными величинами. Каждая пара  ,
, 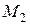 точек на
точек на 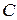 однозначно определяет на
однозначно определяет на 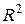 вполне конкретную прямую. Очевидно, что между прямыми, пересекающими фигуру
вполне конкретную прямую. Очевидно, что между прямыми, пересекающими фигуру 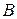 и парами точек на кривой
и парами точек на кривой 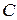 существует взаимно однозначное соответствие. По аналогии со случайными точками, такие прямые также будут называться случайными прямыми.
существует взаимно однозначное соответствие. По аналогии со случайными точками, такие прямые также будут называться случайными прямыми.
|
|
|
Пересечение выпуклой фигуры 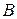 со случайной прямой является отрезком. Далее он будет называться хордой, вырезаемой фигурой
со случайной прямой является отрезком. Далее он будет называться хордой, вырезаемой фигурой 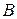 из случайной прямой. Так как длина
из случайной прямой. Так как длина 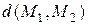 хорды имеет вид
хорды имеет вид
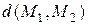 =
= 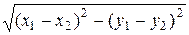 ,
,
то при борелевских 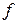 и
и 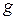 она является случайной величиной. Ее распределение вероятностей
она является случайной величиной. Ее распределение вероятностей 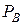 предлагается рассматривать в качестве формы выпуклой фигуры
предлагается рассматривать в качестве формы выпуклой фигуры 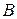 . Две выпуклых фигуры
. Две выпуклых фигуры 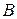 и
и 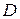 будут считаться одинаковыми по форме, если совпадают распределения вероятностей
будут считаться одинаковыми по форме, если совпадают распределения вероятностей 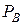 и
и 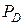 для длин хорд, вырезаемых этими фигурами из случайных прямых.
для длин хорд, вырезаемых этими фигурами из случайных прямых.
Если выбрать на кривой 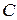 другое начало
другое начало 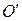 отсчета, то каждая пара
отсчета, то каждая пара 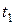 ,
, 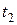 случайных точек из
случайных точек из 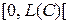 будет определять на кривой
будет определять на кривой 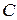 две пары точек. Пару
две пары точек. Пару  ,
, 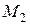 в системе координат с началом в
в системе координат с началом в 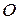 и пару
и пару 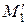 ,
, 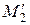 в системе координат с началом в
в системе координат с началом в 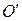 . Длины
. Длины 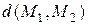 и
и 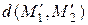 хорд будут, в общем случае, разными. Покажем, что распределение длин хорд будет в обоих случаях одним и тем же.
хорд будут, в общем случае, разными. Покажем, что распределение длин хорд будет в обоих случаях одним и тем же.
Пусть 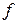 - отображение вида
- отображение вида 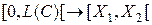 , соответствующее началу отсчета
, соответствующее началу отсчета 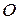 . По предположению
. По предположению 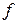 является борелевским отображением. Поэтому
является борелевским отображением. Поэтому 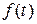 - случайная величина с плотностью
- случайная величина с плотностью
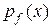 =
= 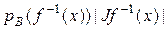 =
= 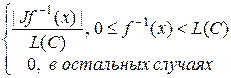
Отметим, что неравенство 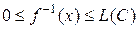 из правой части последнего равенства эквивалентно
из правой части последнего равенства эквивалентно 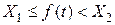 .
.
Пусть 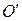 - другое начало отсчета на кривой
- другое начало отсчета на кривой 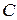 , которому в первой системе координат соответствует точка
, которому в первой системе координат соответствует точка  . Если
. Если 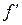 - отображение вида
- отображение вида 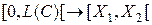 , соответствующее началу отсчета
, соответствующее началу отсчета 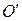 , то для каждой точки
, то для каждой точки 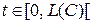 получаем, что
получаем, что 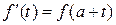 . Из этого равенства следует, что
. Из этого равенства следует, что 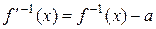 . Поэтому
. Поэтому
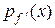 =
= 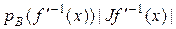 =
= 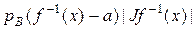 .
.
Или
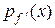 =
= 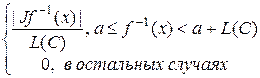 .
.
Неравенство 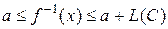 из правой части равенства эквивалентно
из правой части равенства эквивалентно 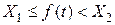 . Поэтому
. Поэтому 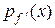 =
= 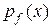 . Что и требовалось доказать. Таким же образом доказывается независимость от выбранного начала отсчета отображения
. Что и требовалось доказать. Таким же образом доказывается независимость от выбранного начала отсчета отображения 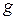 вида
вида 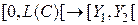 , которое каждой случайной точке
, которое каждой случайной точке 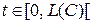 ставит в соответствие вторую координату
ставит в соответствие вторую координату 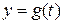 точки
точки 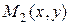 на кривой
на кривой 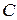 .
.
Покажем, что форма фигуры не меняется при параллельном переносе. Пусть 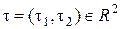 - фиксированный вектор,
- фиксированный вектор, 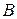 - подмножество на
- подмножество на 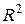 , а
, а 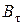 - множество, полученное параллельным переносом
- множество, полученное параллельным переносом 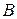 на вектор
на вектор 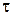 , то есть
, то есть
|
|
|
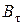 =
= 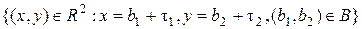 .
.
В этом случае уравнение границы множества 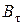 принимает вид
принимает вид
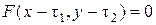 .
.
Если граница множества 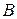 спрямляема, то спрямляема и граница множества
спрямляема, то спрямляема и граница множества 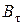 . Таким образом, если
. Таким образом, если 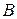 - фигура, то
- фигура, то 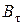 - также фигура и наоборот. Имеет место следующий результат.
- также фигура и наоборот. Имеет место следующий результат.
Теорема 3.6.1. Фигура 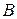 и получаемая из нее параллельным переносом на вектор
и получаемая из нее параллельным переносом на вектор 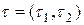 фигура
фигура 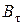 имеют одну и ту же форму, то есть
имеют одну и ту же форму, то есть 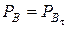 .
.
Теорема 3.6.2. Фигура 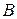 и получаемая из нее поворотом относительно начала координат на угол
и получаемая из нее поворотом относительно начала координат на угол 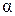 фигура
фигура 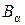 имеют одну и ту же форму, то есть
имеют одну и ту же форму, то есть 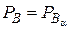 .
.
При повороте относительно произвольной точки 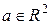 необходимо вначале выполнить параллельный перенос фигуры на вектор -
необходимо вначале выполнить параллельный перенос фигуры на вектор - 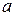 , затем повернуть сдвинутую фигуру относительно начала координат и после выполнить параллельный перенос повернутой фигуры на вектор
, затем повернуть сдвинутую фигуру относительно начала координат и после выполнить параллельный перенос повернутой фигуры на вектор 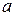 .
.
Таким образом, сравнение фигур 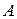 и
и 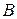 по форме, с формальной точки зрения, заключается в проверке равенства распределений
по форме, с формальной точки зрения, заключается в проверке равенства распределений 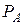 и
и 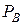 длин хорд, вырезаемых этими фигурами из прямых, выбранных на плоскости случайным образом. Получение для конкретной фигуры
длин хорд, вырезаемых этими фигурами из прямых, выбранных на плоскости случайным образом. Получение для конкретной фигуры 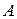 ее распределения
ее распределения 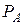 путем теоретических вычислений, в общем случае, может оказаться достаточно сложной задачей. Поэтому в приложениях целесообразно воспользоваться методами математической статистики. Они позволяют проверить равенство
путем теоретических вычислений, в общем случае, может оказаться достаточно сложной задачей. Поэтому в приложениях целесообразно воспользоваться методами математической статистики. Они позволяют проверить равенство 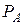 =
= 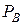 путем исследования случайных выборок, полученных из этих распределений. Отметим, что получение случайных выборок длин хорд, практически, не зависит от вида фигуры.
путем исследования случайных выборок, полученных из этих распределений. Отметим, что получение случайных выборок длин хорд, практически, не зависит от вида фигуры.
В самом деле, пусть 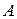 и
и 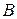 - сравниваемые фигуры, а
- сравниваемые фигуры, а 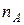 и
и 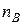 - количество независимых случайные прямых, пересекающих
- количество независимых случайные прямых, пересекающих 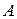 и
и 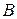 соответственно. Пусть
соответственно. Пусть 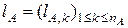 и
и 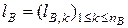 - выборки длин хорд, вырезанных из этих прямых фигурами
- выборки длин хорд, вырезанных из этих прямых фигурами 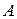 и
и 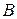 . Предположение о равенстве распределений
. Предположение о равенстве распределений 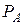 и
и 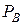 в математической статистике называется гипотезой однородности. Для ее проверки разобьем множество
в математической статистике называется гипотезой однородности. Для ее проверки разобьем множество 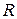 вещественных чисел на
вещественных чисел на 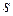 интервалов. Пусть
интервалов. Пусть 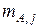 и
и 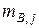 - количество элементов выборок
- количество элементов выборок 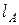 и
и  соответственно, оказавшихся в
соответственно, оказавшихся в 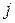 -ом интервале. Известно [68, с. 483], что при равенстве
-ом интервале. Известно [68, с. 483], что при равенстве 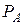 =
= 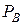 распределение статистики
распределение статистики  вида
вида
 =
= 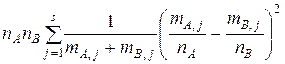 ,
,
стремиться при 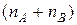
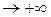 к распределению
к распределению 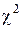 с (
с (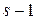 ) степенью свободы. Поэтому вероятность оказаться в интервале
) степенью свободы. Поэтому вероятность оказаться в интервале 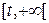 для статистики
для статистики  равняется приблизительно
равняется приблизительно 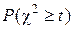 .
.
|
|
|
Сказанное позволяет свести сравнение фигур по форме к проверке гипотезы однородности. В самом деле, зададим малое положительное число 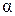 (например, 0.01 или 0.005) и, решив уравнение
(например, 0.01 или 0.005) и, решив уравнение 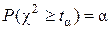 относительно
относительно 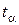 , построим критическую область
, построим критическую область 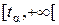 . Если для вычисленного значения статистики
. Если для вычисленного значения статистики  выполняется неравенство
выполняется неравенство 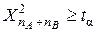 , то гипотеза о равенстве распределений
, то гипотеза о равенстве распределений 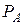 и
и 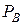 отвергается. Очевидно, что вероятность отвергнуть верную гипотезу равняется
отвергается. Очевидно, что вероятность отвергнуть верную гипотезу равняется 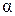 .
.
Наконец, перейдем к описанию формы невыпуклых фигур. Принципиальное отличие невыпуклой фигуры от выпуклой состоит в том, что ее пересечение с прямой линией может состоять из нескольких отрезков, которые так же будут называться хордами. Следовательно, непосредственное применение предложенного выше определения формы для сравнения невыпуклых фигур не подходит.
Поэтому сопоставим каждой невыпуклой фигуре не одну, а пару случайных величин. Первая случайная величина будет описывать число хорд, которые вырезает фигура из прямой линии. Вторая – сумму длин всех хорд, вырезанных из прямой. Таким образом, форму невыпуклой фигуры можно рассматривать как двумерную случайную величину или ее распределение. Две невыпуклые фигуры следует рассматривать как одинаковые по форме, если их распределения совпадают. Очевидно, что фигуры, получаемые друг из друга параллельным переносом или поворотом, будут иметь одну и ту же форму. Если применить определение формы невыпуклой фигуры для описания выпуклых фигур, то случайная величина, описывающая количество вырезанных хорд, будет принимать всегда (с вероятностью равной единице) значение 1. Это означает, что определение формы выпуклой фигуры является частным случаем определения формы невыпуклых фигур. Таким образом, для сравнения двух фигур по форме достаточно получить для каждой из них двумерную выборку и проверить гипотезу однородности.
3.7 Свойства формы фигур на дискретной решетке
При определении формы плоских фигур в 3.6 использовалась вещественная плоскость 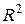 . Однако, исходная информация о сцене представлена, как правило, в виде цифровых изображений. Поэтому при сравнении фигур по форме возникают трудности, вызванные дискретизацией (заменой
. Однако, исходная информация о сцене представлена, как правило, в виде цифровых изображений. Поэтому при сравнении фигур по форме возникают трудности, вызванные дискретизацией (заменой 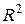 на
на 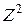 ). Как будет показано ниже, на
). Как будет показано ниже, на 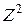 квадраты с разными длинами сторон и круги с разными радиусами могут распознаваться как разные по форме фигуры. Следует помнить и о том, что для вычисления геометрических признаков, в частности формы, необходимо располагать проекцией объекта. В ходе сегментации проекции объектов сцены искажаются. Это проявляется как в виде потери некоторой части собственных пикселей (проекция уменьшается), так и в виде присоединения к проекции пикселей фона (проекция увеличивается). Поэтому рассчитывать на буквальное совпадение проекции присутствующего на сцене объекта с проекцией сравниваемого объекта (образца) не приходится. Следовательно, методы сравнения фигур по форме должны быть терпимыми к определенным искажениям.
квадраты с разными длинами сторон и круги с разными радиусами могут распознаваться как разные по форме фигуры. Следует помнить и о том, что для вычисления геометрических признаков, в частности формы, необходимо располагать проекцией объекта. В ходе сегментации проекции объектов сцены искажаются. Это проявляется как в виде потери некоторой части собственных пикселей (проекция уменьшается), так и в виде присоединения к проекции пикселей фона (проекция увеличивается). Поэтому рассчитывать на буквальное совпадение проекции присутствующего на сцене объекта с проекцией сравниваемого объекта (образца) не приходится. Следовательно, методы сравнения фигур по форме должны быть терпимыми к определенным искажениям.
|
|
|
|
|
Дата добавления: 2015-05-09; Просмотров: 323; Нарушение авторских прав?; Мы поможем в написании вашей работы!