Цифровые компараторы

Цифровой компаратор предназначен для сравнения двух n -разрядных двоичных чисел A ={ a ₁, a ₂,..., a_n } и B ={ b ₁, b ₂,..., b_n }. В результате сравнения может установливаться одно из соотношений: =, ≠; >; <; ≥; ≤. Выходная функция F принимает единичное значение, если проверяемое соотношение выполняется или нулевое – если не выполняется. Цифровой компаратор позволяет реализовывать ту часть алгоритма измерения в цифровой измерительной технике, в которой заложена процедура сравнения неизвестного значения измеряемой величины с цифровой мерой. Рассмотрим синтез компаратора для реализации функции равенства двух n -разрядных двоичных кодов. Факты равенства, больше и меньше отдельных разрядов определим функциями f _{( A=B ) i}, f _{( A>B ) i} и f _{( A<B ) i}, заданной следующей таблицей истинности 8.9:

Таблица 8.9.

Входы	Выходы
ai	bi	f ( A=B ) i	f ( A>B ) i	f ( A<B ) i

Тогда факт неравенства разрядов будет определяться инверсным значением функции 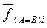. Определим ФАЛ для f _{( A=B ) i}, соответствующую приведенной таблице истинности

.

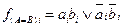Синтезированная структурная схема в соответствии с формулой для f _{( A=B ) i} имеет вид, представленный рис. 8.22.

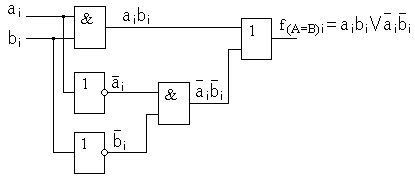
Рис. 8.22. Функциональная схема устройства сравнения одноразрядных кодов.

Выполним следующие преобразования над функцией f _{( A=B ) i}, используя тождества алгебры логики:

,

т.е. окончательно имеем инверсию функции исключающее ИЛИ.

Функция неравенства одного разряда 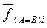тогда будет выражаться через прямое значение функции Исключающее ИЛИ. Для перехода от равенства (неравенства) отдельных разрядов к функции равенства F _{( A = B )} (неравенства ) всего n -разрядного кода необходимо установить факт наличия логических единиц во всех функциях f _{( A=B ) i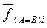} (). Это осуществляется n -входовым элементом И. ФАЛ для функции F _{( A = B )} с учетом использования функции инверсии исключающего ИЛИ имеет вид

.

Функция f _{( A>B ) i} одноразрядного числа согласно таблице 8.9 будет реализовываться двухвходовым элементом И, на один вход которого будет подаваться разряд a_i в прямом виде, а на второй – разряд 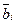в инверсном виде, т.е. 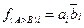. Несколько сложнее обстоит дело со схемой сравнения n -разрядных слов на «больше». Для этого анализ неравенства должен выполняться последовательно в направлении от старших разрядов в сторону младших. Младшие разряды сравниваются при условии равенства старших. Тогда логика сравнения на «больше» для двухразрядного слова с учетом равенства/неравенства старшего разряда может быть представлена в следующем виде

.

Аналогично можно записать логику сравнения для трехразрядного числа

и четырехразрядного числа

.

В общем случае функция сравнения на «больше» для произвольного n -разрядного числа можно выразить

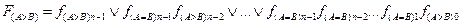
Подставив минтермы функций f _{( A>B ) i} в переменных a_i и b_i и эквивалентные функциям f _{( A=B ) i} элементы исключающее ИЛИ-НЕ, можно реализовать представленную ФАЛ для F _{( A>B )}.

Функцию сравнения на «меньше» можно определить как

,

т.е. только если будет отсутствовать факт равенства F _{( A = B )}=0 и факт больше F _{( A > B )}=0, то схемой совпадения нулей (функцией ИЛИ) установится общий ноль, а инверсия этого нуля даст единичное значение функции F _{( A < B )} как последнего оставшегося варианта сравнения.

Пример схемы, реализующей рассмотренные выше функции F _{( A = B )}, F _{( A > B )} и F _{( A < B )} двух четырехразрядных чисел приведен на рис.8.23.

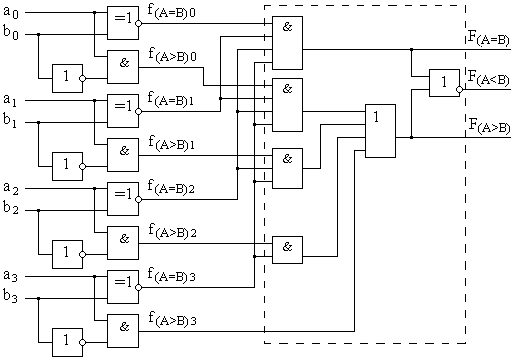
Рис.8.23. Функциональная схема компаратора, реализующего функции «равно», «больше», «меньше» двух четырехразрядных чисел.

Из-за громоздкости структуры компараторов чисел большой разрядности и необходимости использования в этом случае логических элементов с большим количеством входов, в интегральном исполнении обычно реализуются компараторы, сравнивающие двоичные коды с разрядностью n не более 4 или 8 бит. Для повышения разрядности обрабатываемых кодов сравниваемые слова разбиваются на группы фиксированной разрядности с индивидуальными выходами функций сравнения на «равно» F _{( A=B ) i} и «больше» F _{( A > B ) i} в каждой группе. Тогда описанный выше метод применим и для анализа n -разрядных кодов. Для этого выходы функций равенства и больше компараторов отдельных групп объединяются в часть схемы рис.8.23, заключенную в пунктирную линию. В результате формируется результат сравнения кодов всей длины. В условном графическом обозначении функция компаратора задается символами «= =» или «COMP».

В качества примера можно привести микросхему четырехразрядного компаратора К561ИП2, реализующую функции сравнения на «больше», «меньше» и «равно». Эта микросхема может также применяться для сравнения кодов большей разрядности (рис.8.24). Для этого в ней предусмотрены входы переноса функций «меньше» и «равно», на которые подаются выходы одноименных функций группы младших разрядов. Вход «больше» в данной микросхеме избыточен, и на него в микросхемах всех групп необходимо постоянно подавать потенциал логической единицы. На вход «меньше» микросхемы самой младшей группы необходимо подать логический ноль, а на вход «равно» - логическую единицу. Такое же включение микросхемы должно быть и при использовании ее для сравнения четырехразрядных слов.

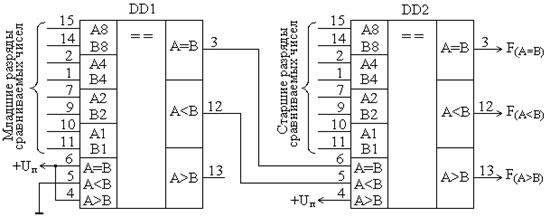
Рис.8.24. Включение микросхемы К561ИП2 при повышения разрядности сравниваемых слов.

Дата добавления: 2015-05-09