
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определения. Числовые характеристики статистического распределения (выборочные среднее, дисперсия, среднеквадратичное отклонение
|
|
|
|
Числовые характеристики статистического распределения (выборочные среднее, дисперсия, среднеквадратичное отклонение, мода, медиана, моменты, асимметрия и эксцесс, квантили).
Асимптотические свойства эмпирической функции распределения
1. По усиленному закону больших чисел 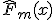 сходится почти наверное к теоретической функции распределения
сходится почти наверное к теоретической функции распределения  :
:
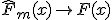 почти наверное при
почти наверное при 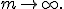
2. Выборочная функция распределения является асимптотически нормальной оценкой функции распределения  при условии, что
при условии, что 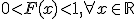 :
:
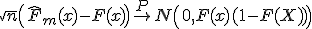 при
при 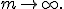
Вы́борочное (эмпири́ческое) сре́днее — это приближение теоретического среднего распределения, основанное на выборке из него.
Пусть 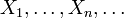 — выборка из распределения вероятности. Тогда
— выборка из распределения вероятности. Тогда
§ Выборочная дисперсия — это случайная величина
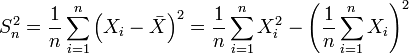 ,
,
где символ 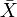 обозначает выборочное среднее.
обозначает выборочное среднее.
§ Несмещённая (исправленная) дисперсия — это случайная величина
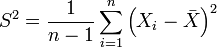 .
.
[править]Замечание
Очевидно,
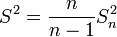 .
.
[править]Свойства выборочных дисперсий
§ Выборочная дисперсия является теоретической дисперсией выборочного распределения. Более точно, пусть 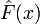 —выборочная функция распределения данной выборки. Тогда для любого фиксированного
—выборочная функция распределения данной выборки. Тогда для любого фиксированного 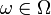 функция
функция 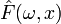 является (неслучайной) функцией дискретного распределения. Дисперсия этого распределения равна
является (неслучайной) функцией дискретного распределения. Дисперсия этого распределения равна 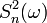 .
.
§ Обе выборочные дисперсии являются состоятельными оценками теоретической дисперсии. Если 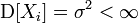 , то
, то
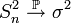
и
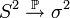 ,
,
где 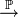 обозначает сходимость по вероятности.
обозначает сходимость по вероятности.
§ Выборочная дисперсия является смещённой оценкой теоретической дисперсии, а исправленная выборочная дисперсия несмещённой:
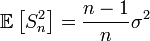 ,
,
и
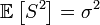 .
.
§ Выборочная дисперсия нормального распределения имеет распределение хи-квадрат. Пусть  . Тогда
. Тогда
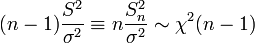 .
.
|
|
|
|
|
Дата добавления: 2015-05-09; Просмотров: 522; Нарушение авторских прав?; Мы поможем в написании вашей работы!