Корреляционный момент и коэффициент корреляции

Вопрос 26

Рассмотрим вопрос о статистической зависимости случайных ве­личин.

Любые две случайные величины, входящие в систему, являются не­зависимыми или зависимыми. Поскольку степень взаим­ной зависимости может быть различной, целесообразно ввести количественную меру взаимной зависимости. В ка­честве такой меры могут служить корреляционный мо­мент и коэффициент корреляции (связи), к определению которых мы и перейдем.

Рассмотрим две дискретные случайные величины: Х и У. Пусть их возможные значения соответственно равны:

х₁, х_2,х₃,… х_i, …x_s

y₁, y₂, y_3,…y_j,… y_r

Среднее значение первой величины составляет х и второй - у. Введем в рассмотрение отклонения воз­можных значений случайных величин от их средних зна­чений, которые будем

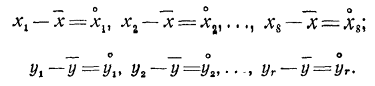
коротко обозначать следующим образом:

В свое время (см. §6 гл. 3) говорилось, что среди отклонений имеются числа как положительные, так и отрицательные. Вероятности отклонений равны вероятностям

соответствующих значений случайных величин, т. е.

o o

P(x_i -x) =P(х_i)=P(х_i) и Р(у_j - у) =Р(у_j)=Р(у_i)

Если средние значения у случайных величин X или Y равны нулю, то их отклонения x_i и y_j равны соответствующим значениям случайных величин.

Положим далее, что известны условные и безусловные законы распределения случайных величин Х и Y и закон распределения системы этих дискретных величин Р(x_i,y_j).

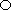Перемножим все возможные отклонения одной случайной величины x_i почленно на все возможные отклонения друтой y_j с учетом их вероятностей и все произведения сложим. В итоге получим величину, которая в виде общей формулы может быть записана следующим

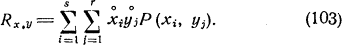
образом:

Индексы суммирования i, j указывают, что в сумму должны быть включены все возможные

о о

сочетания значений x_i и y_j.

о о

Величина R_x,y представляет собой среднее значеи е произведений x_iна y_j и называется в теории вероятностей корреляционным моментом.

На основании формулы умножения вероятностей случайных величин (93), учитывая, что

выражение (103) для корреляционного момента можно также записать в виде

(104)

Выражения, аналогичные (103) и (104), могут быть написаны для случая, когда величины Х и Y непрерывны. Заменив суммы интегралами, а вероятности – элементами вероятностей, для непрерывных величин запишем:

Коэффициентом корреляции между двумя случайными величинами, или, иначе, нормированным корреляционным моментом, называется отношение корреляционного момента R_xy к произведению среднеквадратических отклонений случайных величин s_х и s_y:

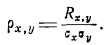
Корреляционный момент, как видно из выражений (103) и (105), является величиной размерной. Размерность его равна произведению размерностей отдельных случайных величин. Коэффициент корреляцииr_x,y - величина безразмерная. R _x,y отличается от r_x,y постоянным (для данных случайных величин) множителем 1/s_x s_y.

Рассмотрим, какими свойствами обладают корреляционный моментRx,y и коэффициент корреляции r. Для этого возвратимся к формуле (104). Положим сначала, что случайные величины Х и Y независимы. Тогда

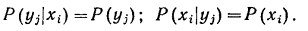
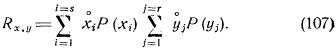
На основании (104) можем записать:

Вторая сумма в правой части равенства (107), не зависящая в данном случае от х_i, представляет собой среднее значение отклонений случайной величины Y в одну и другую стороны от ее среднего значения. Эта величина равна нулю, что следует из факта симметричности положительных и отрицательных отклонений случайной величины относительно среднего значения при учете соответствующих вероятностей. Следовательно, в данном случае R_xy = 0, т. е. если величины независимы, то их корреляционный момент равен нулю. Этот результат понятен. Поскольку мы перемножаем положительные и отрицательные отклонения двух независимых величин с учетом их «весовых» вероятностных коэффициентов, получим в равной мере как положительные, так и отрицательные результаты перемножений. При суммировании они взаимно компенсируются и дают нуль.Следовательно, если величины независимы, равен нулю и коэффициент корреляции:

(108’)

Рассмотрим теперь другой крайний случай, когда величины Х и Yсвязаны жесткой линейной зависимостью вида:

y=kx, (109)

где k — постоянный коэффициент.

При такой зависимости очевидно, что случайные величины принимают всегда согласованные значения, различающиеся только масштабным коэффициентом k.

Если величина Х принимает какое-либо значение х_i, то другая величина Y с условной вероятностью Р(y_j / x _i), равной 1, принимает значение y_j= kx_i. Все другие значения y исключаются. Поэтому при заданном x_i, можно записать

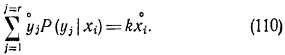
Подставив это значение суммы в (104), получим:

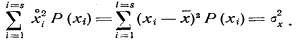
Но

Следовательно, в данном случае

где s_x ² — дисперсия случайной величины X.

Можно далее показать, что если одна случайная величина Y принимает значения, каждый раз в k раз большие (меньшие), чем другая случайная величина X, то дисперсия ее в k² больше (меньше), чем у X:

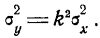
Соответственно 6_y = ± k 6_x. Поэтому значение корреляционного момента (111) может быть переписано в виде

Знак плюс в правой части равенства соответствует случаю, когда k положительно, минус—когда оно отрицательно.
Таким образом, мы установили, что корреляционный момент в случае линейной функциональной связи между величинами по абсолютному значению равен произведению среднеквадратических отклонений случайных величин. Коэффициент корреляции при этом равен

Следовательно, в двух крайних случаях связи между случайными величинами коэффициент корреляции оказался равным по абсолютному значению нулю и единице: значение нуль соответствует отсутствию связи, а единица—наиболее тесной (линейной функциональной)
связи между величинами.
Естественно предположить, что в промежуточных случаях, когда связь существует, но не является предельно жесткой, коэффициент корреляции должен иметь

величину, лежащую в промежутке между крайними значениями, т. е. между 0 и ±1. Таким образом, подтверждается, что корреляционный момент и коэффициент корреляции могут служить мерой связи между случайными величинами. Знак плюс у коэффициента корреляции, если величины не жестко связаны, говорит о том, что когда отклонение у одной случайной величины положительно, то оно преимущественно положительно и у другой величины. Если отклонение отрицательно, то оно в большинстве случаев отрицательно у обеих случайных величин. Знак минус говорит, наоборот, о преимущественно разных знаках отклонений у двух случайных величин X и Y.

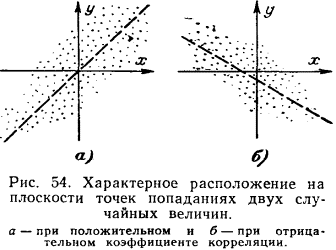
На рис. 54 для примера показаны точки, полученные при совместных измерениях значений двух случайных величин.

Отметим, что речь идет о линейной связи между величинами. Можно показать, что при нелинейной связи, например вида y = k x, при симметричном законе распределения х, когда

положительные и отрицательные отклонения равновероятны, коэффициент корреляции равен нулю, хотя случайные величины связаны при этом функционально жестко.

Иначе говоря, если коэффициент корреляции равен нулю, это говорит, несомненно, только об отсутствии линейной связи. Однако если связь между величинами (какая бы то ни была) отсутствует (т. е. величины независимы), коэффициент корреляции всегда равен нулю.

В первом случае (рис. 54,а) расположение точек позволяет сделать предположение о наличии положительной корреляции между величинами, а во втором (рис. 54,6) — отрицательной. Пунктиром приблизительно показаны линии, на которые должны были бы ложиться точки в случае, если бы имела место функциональная линейная связь между величинами Х.и Y. На рис. 55 показано характерное расположение точек, ког-

да величины независимы и, следовательно, не коррелироваиы.

Упражнение.

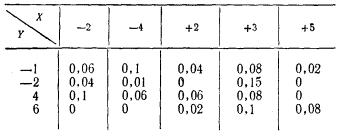
Определить корреляционный момент и коэффициент корреляции между двумя дискретными, случайными величинами Х и Y, двухмерный закон распределения вероятностей которых задан таблицей.

Ответ: 2,05; 0,208.

Дата добавления: 2015-05-26